2020八年级数学上册第十二章全等三角形12 3页

第十二章 12.1全等三角形 知识点1：全等形与全等三角形的概念 ‎ 定义:能够完全重合的两个图形叫做全等形.‎ 能够完全重合的两个三角形叫做全等三角形,重合的顶点叫做对应点,重合的边叫做对应边,重合的角叫做对应角.全等三角形是最简单的全等形.‎ 关键提醒:1. 全等三角形是特殊的全等形,全等三角形关注的是两个三角形的形状和大小是否完全一样,叠合在一起是否重合,与它们的位置没有关系.‎ ‎2. “全等”用“≌”表示,读作“全等于”,记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.‎ ‎3. 一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等,所以两个全等的三角形都能通过适当的平移、翻折、旋转等变换后重合.‎ 知识点2：全等三角形的性质 ‎ 全等三角形的对应边相等、对应角相等.由全等三角形的定义还容易知道全等三角形的周长相等、面积相等、对应边上的中线相等、对应角的平分线相等、对应边上的高相等.‎ 关键提醒:1. 全等三角形的周长相等,面积相等,但周长相等或面积相等的两个三角形不一定是全等三角形.‎ ‎2. 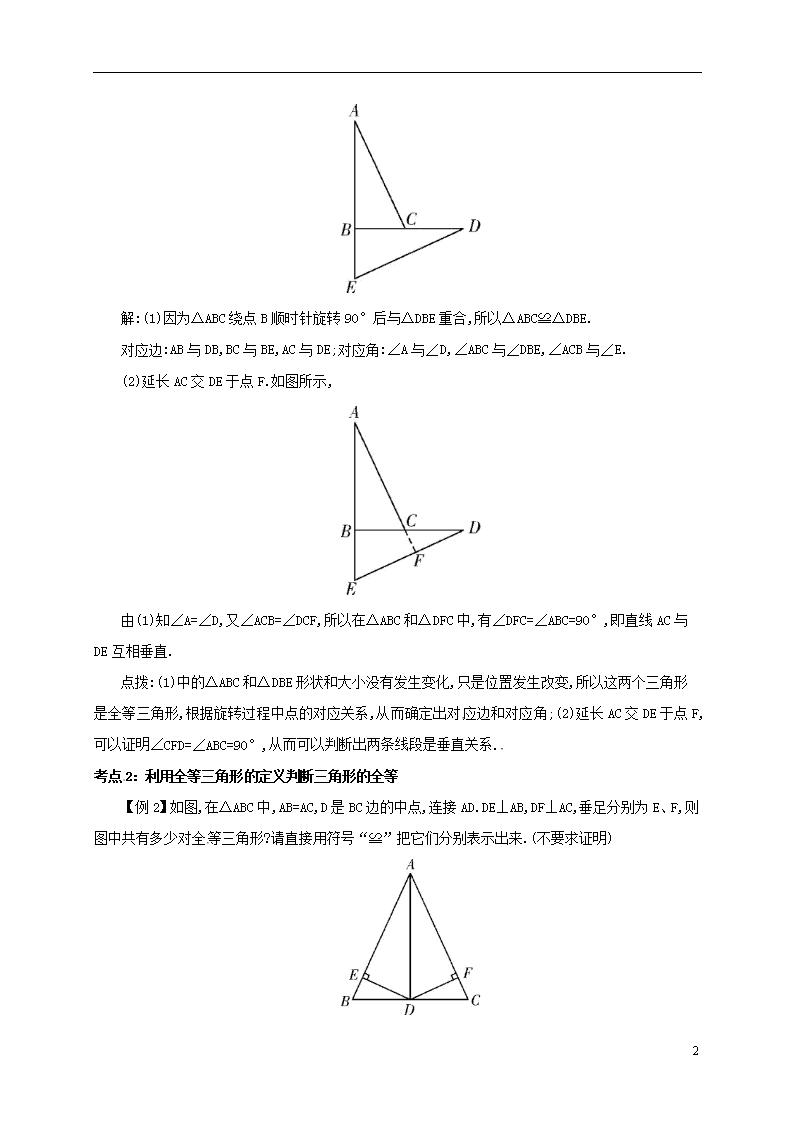要正确区分对应边与对边、对应角与对角的概念.一般地,对应边、对应角是就两个三角形而言的,指两条边、两个角的关系,而对边、对角是就同一个三角形的边和角而言的,对边是指角的对边,对角是指边的对角.‎ 考点1：全等三角形的对应边和对应角判定 ‎【例1】如图所示,△ABC绕点B顺时针旋转90°到△DBE,且∠ABC=90°.‎ ‎(1)△ABC和△DBE是否全等?若全等,指出对应边和对应角;‎ ‎(2)直线AC、DE有怎样的位置关系?‎ 3‎ 解:(1)因为△ABC绕点B顺时针旋转90°后与△DBE重合,所以△ABC≌△DBE.‎ 对应边:AB与DB,BC与BE,AC与DE;对应角:∠A与∠D,∠ABC与∠DBE,∠ACB与∠E.‎ ‎(2)延长AC交DE于点F.如图所示,‎ 由(1)知∠A=∠D,又∠ACB=∠DCF,所以在△ABC和△DFC中,有∠DFC=∠ABC=90°,即直线AC与DE互相垂直.‎ 点拨:(1)中的△ABC和△DBE形状和大小没有发生变化,只是位置发生改变,所以这两个三角形是全等三角形,根据旋转过程中点的对应关系,从而确定出对应边和对应角;(2)延长AC交DE于点F,可以证明∠CFD=∠ABC=90°,从而可以判断出两条线段是垂直关系.‎ 考点2：利用全等三角形的定义判断三角形的全等 ‎【例2】如图,在△ABC中,AB=AC,D是BC边的中点,连接AD.DE⊥AB,DF⊥AC,垂足分别为E、F,则图中共有多少对全等三角形?请直接用符号“≌”把它们分别表示出来.(不要求证明)‎ 3‎ 解:图中共有3对全等三角形,它们分别是:△ADE≌△ADF,△ADB≌△ADC,△BDE≌△CDF.‎ 点拨:本题通过观察就可得到,主要考查学生的观察能力.另外,在小学里,我们已经学过等腰三角形关于底边上的中线所在的直线对称,从这个角度去分析,很快也能得到答案.‎ 考点3：全等三角形性质的应用 ‎【例3】如图所示,A、D、E三点在同一直线上,且△BAD≌△ACE.‎ ‎(1)试说明BD=DE+CE;‎ ‎(2)当△ABD满足什么条件时,BD∥CE?‎ 解:(1)∵　△BAD≌△ACE,‎ ‎∴　BD=AE,AD=CE.‎ 又A、D、E三点在同一直线上,‎ ‎∴　AE=AD+DE,‎ 即BD=DE+CE.‎ ‎(2)当△ABD满足∠ADB=90°时,BD∥CE.‎ 点拨:本题主要考查全等三角形性质的应用.‎ ‎(1)由△BAD≌△ACE知,BD=AE,AD=CE,‎ 又A、D、E三点在同一直线上,借助线段的和差及线段的等量转化即可得到结论.‎ ‎(2)根据平行线的性质,只要∠BDE=∠E,便可得到BD∥CE,这时只需BD⊥AE或∠ADB=90°即可.‎ ‎ ‎ ‎ ‎ ‎ ‎ 3‎