湖南省株洲市茶陵县2020届九年级上学期期末考试数学试题 13页

九年级上期期末质量检测数学试题卷（2020.1）‎ 时量：120分钟 满分：150分 一、选择题（每小题有且只有一个正确答案，本题共10小题，每小题4分，共40分）：‎ ‎1．抛物线的顶点坐标是（ ） ‎ A． B． C． D．‎ ‎2．若，则下列各式一定成立的是 （ ） ‎ A． B． C． D．‎ ‎3．在Rt△ABC中，∠C=90°，如果，那么的值是 ( )‎ ‎ A．90° B．60° C．45° D．30°‎ ‎4．某排球场6名队员的身高（单位：cm）分别是180，184，188，190，192，194. 现用一名身高为186cm的队员换下场上身高为192cm的队员，与换人前相比，场上队员的身高 ( )‎ A. 平均数变小，方差变小 B. 平均数变小，方差变大 C. 平均数变大，方差变小 D. 平均数变大，方差变大 ‎5．方程的解是 （ ）‎ A． B． C． D．‎ ‎6．在△ABC中，∠C=90°，AB=5，BC=4，以A为圆心，以3为半径画圆，‎ 则点C与⊙A的位置关系是 （ ）‎ A. 在⊙A外 B. 在⊙A上 C. 在⊙A内 D. 不能确定 ‎7．已知点都在反比例函数的图像上，那么（ ）‎ A. B. C. D. 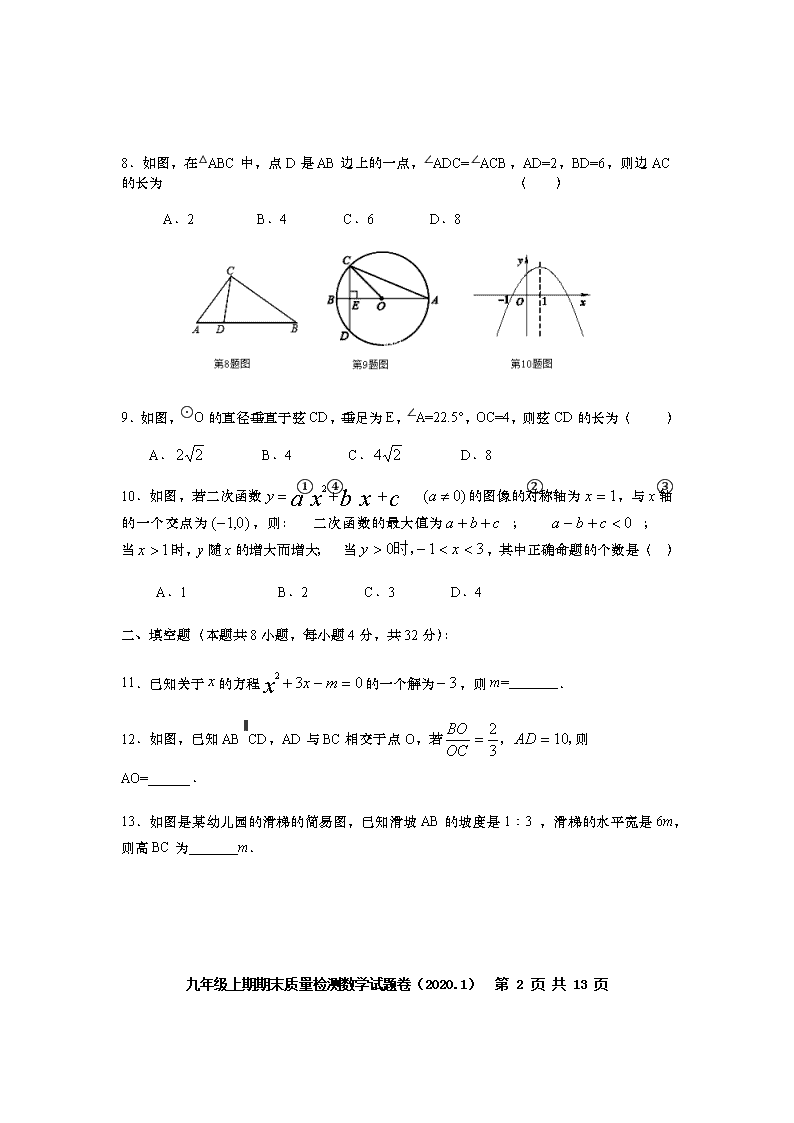的大小无法确定 九年级上期期末质量检测数学试题卷（2020.1） 第 13 页 共 13 页 ‎8．如图，在△ABC中，点D是AB边上的一点，∠ADC=∠ACB，AD=2，BD=6，则边AC的长为 （ ）‎ ‎ A．2 B．4 C．6 D．8‎ ‎9．如图，⊙O的直径垂直于弦CD，垂足为E，∠A=22.5°，OC=4，则弦CD的长为（ ） ‎ A． B．4 C． D．8‎ ‎10．如图，若二次函数的图像的对称轴为，与x轴的一个交点为，则：①二次函数的最大值为 ；② ；③ 当时，y随x的增大而增大；④当，其中正确命题的个数是（ ） ‎ ‎ A．1 B．2 C．3 D．4‎ 二、填空题（本题共8小题，每小题4分，共32分）：‎ ‎11．已知关于的方程的一个解为，则m= ．‎ ‎12．如图，已知AB∥CD，AD与BC相交于点O，若则AO=______．‎ ‎13．如图是某幼儿园的滑梯的简易图，已知滑坡AB的坡度是1︰3 ，滑梯的水平宽是6m，则高BC为_______m． ‎ 九年级上期期末质量检测数学试题卷（2020.1） 第 13 页 共 13 页 ‎14．如图，A、B、C是⊙O上的点，若∠AOB=100°，则∠ACB= .‎ ‎15．已知△ABC∽△DEF，且 ，且△ABC与△DEF的周长和为175 ，则△ABC 的周长为 ．‎ ‎16．在元旦的一次同学聚会上，每人都向其他人赠送了一份小礼品，共互送110份礼品，则参加聚会的有 名同学．‎ ‎17．已知，是方程的两个实根，则 ． ‎ ‎18．如图所示，在△ABC中，BC=6，E，F分别是AB，AC的中点，动点P在射线EF上，BP交CE于点D， ∠CBP的平分线交CE于点Q。当时，EP+BP= ．‎ 三、解答题（本大题共8小题，共78分）：‎ ‎19．（本小题满分6分）计算：‎ ‎ ‎ 九年级上期期末质量检测数学试题卷（2020.1） 第 13 页 共 13 页 ‎20．（本小题满分8分，每小题4分）解下列方程：‎ ‎（1）. （2）. ‎ 人数 C B A 成绩 ‎50‎ ‎40‎ ‎30‎ ‎20‎ ‎10‎ ‎21．（本小题满分8分）某学校从360名九年级学生中抽取了部分学生进行体育测试，并就他们的成绩(成绩分为A、B、C三个层次)进行分析，绘制了频数分布表与频数分布直方图(如图)，请根据图表信息解答下列问题：‎ ‎ ‎ 分组 频数 频率 C ‎10‎ ‎0.10‎ B ‎0.50‎ A ‎40‎ 合计 ‎1.00‎ ‎ ‎ ‎（1）补全频数分布表与频数分布直方图；‎ ‎（2） 如果成绩为A层次的同学属于优秀，请你估计该校九年级约有多少人达到优秀水平？‎ 九年级上期期末质量检测数学试题卷（2020.1） 第 13 页 共 13 页 ‎22．（本小题满分10分）如图，点E是弧BC的中点，点A在⊙O上，AE交BC于点D。‎ ‎（1）求证：； ‎ ‎ （2）连接OB，OC，若⊙O 的半径为5，BC=8，求△OBC的面积。‎ ‎ ‎ ‎23．（本小题满分10分）如图，在Rt△ABC中，∠C=90°，BC=8，，点D在BC上，且BD=AD. ‎ ‎（1）求AC的长； （2）求的值．‎ 九年级上期期末质量检测数学试题卷（2020.1） 第 13 页 共 13 页 ‎24．（本小题满分10分）如图，某反比例函数图像的一支经过点和点B（点B在点A的右侧），作BC⊥y轴，垂足为点C，连接AB，AC。‎ ‎（1）求该反比例函数的解析式；‎ ‎（2）若△ABC的面积为6，求直线AB的表达式。‎ ‎ ‎ ‎25．（本小题满分13分）如图，正方形ABCD的边长为1，点E是AD边上的动点，从点A沿AD向点D运动，以BE为边，在BE的上方作正方形BEFG，连接CG． （1）求证： △AEB≌△CGB；‎ 九年级上期期末质量检测数学试题卷（2020.1） 第 13 页 共 13 页 ‎（2）若设AE=x，DH=y，当x取何值时，y有最大值？并求出这个最大值； （3）连接BH，当点E运动到AD的何位置时有△BEH∽△BAE？‎ ‎ ‎ ‎26.（本小题满分13分）已知△ABC为直角三角形，∠ACB=90°，AC=BC，点A、C在x轴上，点B坐标为(3，m)（m>0），线段AB与y轴相交于点D，以P(1，0)为顶点的抛物线过点B、D。 ‎ ‎（1）求点A的坐标（用m表示）； ‎ ‎（2）求抛物线的解析式；‎ ‎（3）设点Q为抛物线上点P至点B之间的一动点，连结PQ并延长交BC于点E，连结BQ并延长交AC于点F，试证明：FC(AC+EC)为定值．‎ ‎ ‎ ‎ ‎ 九年级上期期末质量检测数学试题卷（2020.1） 第 13 页 共 13 页 九年级上期期末质量检测数学试题卷（2020.1） 第 13 页 共 13 页 ‎ 九年级上期期末质量检测数学参考答案（2020.1）‎ 一、选择题（本题共10个小题，每小题4分，满分40分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 D B C A D B C B C B 二、填空题（本题共8个小题，每小题4分，满分32分）‎ ‎11、0； 12、 4 ； 13、2 14、 130°；‎ ‎15、75； 16、11 ； 17、27 ； 18、12‎ 三、解答题（本大题共8小题，共78分）‎ ‎19．（本小题满分6分）‎ 解：原式= ………..6分 （每个式子化简各1分，求和3分）‎ ‎ 20. （本小题满分8分）‎ 解：（1）原方程可化为： ……………..2分 ‎ 解得： …………….4分 ‎（2）∵由 ∴ ……………..2分 解得： ……………..4分 ‎（其它解法同样给分） ‎ ‎21．（本小题满分8分）‎ 解：（1）‎ 分组 频数 频率 九年级上期期末质量检测数学试题卷（2020.1） 第 13 页 共 13 页 C ‎10‎ ‎0.10‎ B ‎50‎ ‎0.50‎ A ‎40‎ ‎0.40‎ 合计 ‎100‎ ‎1.00‎ ‎……………..3分（每空1分）‎ 补全直方图略。 ……………..4分（补图1分）‎ ‎（2）∵A层次的同学人数为40人，频率为0.40‎ ‎∴估计该校九年级约有 0.4×360=144人达到优秀水平。………… 8分 ‎22.（本小题满分10分）‎ ‎（1）证明：∵点E是弧BC的中点 ∴∠BAE=∠CBE=∠DBE ……..2分 又∵∠BEA=∠DEB ∴△AEB∽△BED ∴ ……..6分 ‎（2）过点O作OF⊥BC于点F，则BF=CF=4 ……..7分 在中， ……9分 ‎∴ ……10分 ‎23．（本小题满分10分）‎ 解：（1）由∠C=90°，BC=8，得：‎ ‎….4分 ‎(2)设 九年级上期期末质量检测数学试题卷（2020.1） 第 13 页 共 13 页 在Rt△ACD中，‎ ‎ ……..8分 则：CD=3，AD=5 于是： ……10分 ‎24.（本小题满分10分）‎ 解：（1）设反比例函数的解析式为，由它的图像经过点得：‎ 于是该该反比例函数的解析式为 ……4分 ‎（2）由BC⊥y轴，垂足为点C可设，则.于是BC=m,点A到BC的距离为（3－n）.由点B在反比列函数的图像上且△ABC的面积为6可得：‎ ‎ ∴ ……7分 设直线AB的表达式为.将点，代入直线表达式可得：‎ ‎ ∴直线AB的表达式为 ……10分 ‎25.（本小题满分13分）‎ ‎ （1）证明： 由已知∠ABE+∠EBC=∠CBG+∠EBC=90°可得：∠ABE=∠CBG ..2分 九年级上期期末质量检测数学试题卷（2020.1） 第 13 页 共 13 页 在△AEB和△CGB中：∠BAE=∠BCG=90°，AB=BC ， ∠ABE=∠CBG ‎∴△AEB≌△CGB （ASA） ……..4分 ‎（2）∵四边形ABCD，四边形BEFG均为正方形 ∴∠A=∠D=90°, ∠HEB=90°‎ ‎∴∠DEH+∠AEB=90°，∠DEH+∠DHE=90° ∴∠DHE=∠AEB …..6分 ‎∴△ABE∽△DEH 于是 故当 ‎ ……9分 ‎（3）当点E是AD的中点时有 △BEH∽△BAE。 ……10分 理由：∵ 点E是AD的中点时由（2）可得 又∵△ABE∽△DEH ‎ ‎ ∴，又∵ ∴ 又∠BEH=∠BAE=90°‎ ‎∴△BEH∽△BAE ……13分 ‎（其他证明方法同样给分）‎ ‎26.（本小题满分13分）‎ 解：（1）由B (3，m)可知OC=3，BC=m，又△ABC为等腰直角三角形，∴AC=BC=m OA=m﹣3，所以点A的坐标为（3﹣m，0） ……2分 ‎（2）∵∠ODA=∠OAD=45°∴OD=OA= m﹣3，则点D的坐标是（0，m﹣3）‎ 又抛物线的顶点为P(1，0)，且过B、D两点，所以可设抛物线的解析式为：‎ 九年级上期期末质量检测数学试题卷（2020.1） 第 13 页 共 13 页 得：‎ ‎ ∴抛物线的解析式为： ……6分 ‎ 证明：（3）过点Q作QM⊥AC与点M，过点Q作QN⊥BC与点N，设点Q的坐标是 则 ……8分 ‎∵QM∥CE ∴△PQM∽△PEC 则 ‎…..10分 ‎∵QN∥FC ∴△BQN∽△BFC 则 ‎…..12分 又∵AC=4 ∴‎ 即 ……13分 九年级上期期末质量检测数学试题卷（2020.1） 第 13 页 共 13 页