2020八年级数学上册 第12章 整式的乘除 12 3页

‎12.3.1‎‎ 两数和乘以这两个数的差 ‎【学习目标】‎ ‎1、从已有的整式乘法的知识中提炼出两数和乘以它们的差这一乘法公式，明确这一公式来源于整式乘法，又可以用于整式的乘法的辩证思想；‎ ‎2、掌握两数和乘以它们的差的公式的结构，并能正确地运用；‎ ‎【学习重难点】‎ ‎1、掌握两数和乘以它们的差的结构特征；‎ ‎2、正确理解两数和乘以它们的差的公式意义。‎ ‎【学习过程】‎ 一、课前准备 ‎1、多项式与多项式相乘法则 ‎ ‎ ‎ ‎2．利用多项式与多项式的乘法法则写出 (x＋a)(x＋b)的结果。‎ ‎3.计算：‎ ‎(1)(x＋3)(x－3)； 　　 (2)(a＋2b)(a－2b)；‎ ‎(3)(‎4m＋n)(‎4m－n)； (4)(5＋4y)(5－4y)。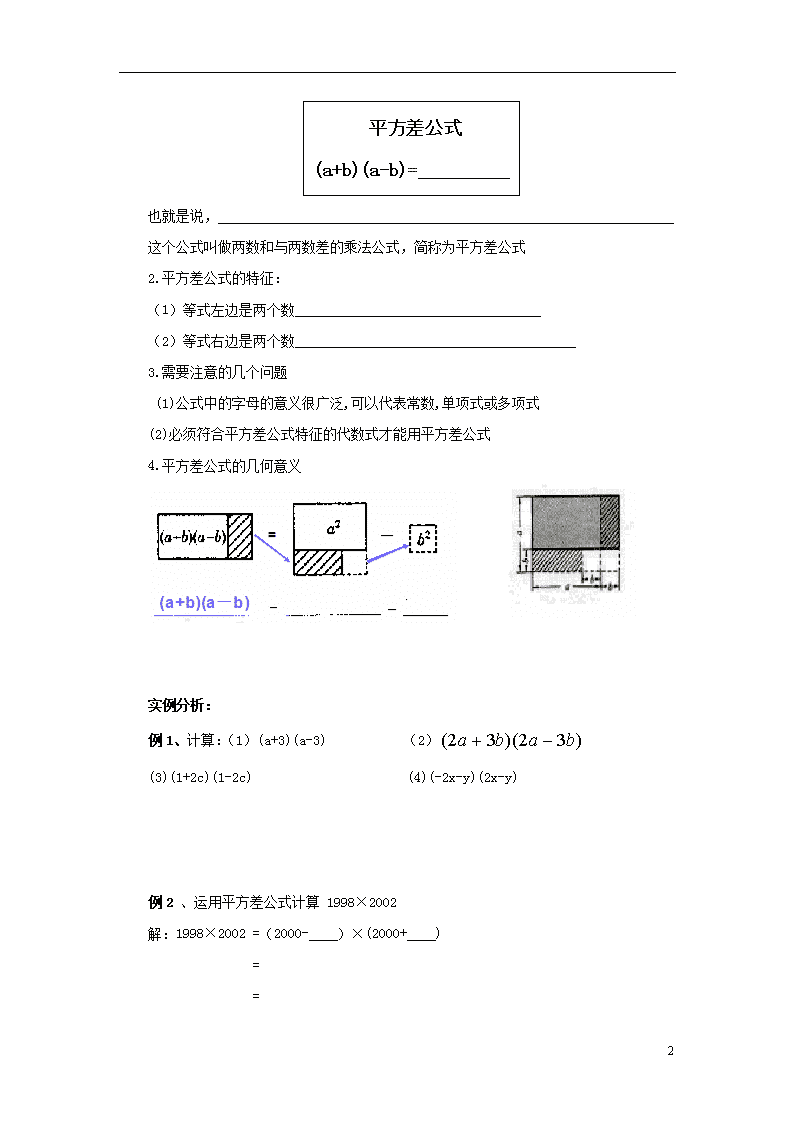‎ 二、学习新知 自主学习：‎ ‎1、做一做，计算 ‎(x ＋ 3)(x － 3)=‎ ‎(a＋2b)(a－2b)=‎ ‎(‎4m＋n)(‎4m－n)=‎ ‎(5＋4y)(5－4y)=‎ ‎(a ＋ b)(a－b)=‎ 归纳总结 3‎ 平方差公式 ‎(a+b)(a-b)= ‎ 也就是说， ‎ 这个公式叫做两数和与两数差的乘法公式，简称为平方差公式 ‎2.平方差公式的特征：‎ ‎（1）等式左边是两个数 ‎ ‎（2）等式右边是两个数 ‎ ‎3.需要注意的几个问题 ‎ (1)公式中的字母的意义很广泛,可以代表常数,单项式或多项式 ‎ ‎(2)必须符合平方差公式特征的代数式才能用平方差公式 ‎4.平方差公式的几何意义 实例分析：‎ 例1、计算：（1）(a+3)(a-3) （2）‎ ‎(3)(1+‎2c)(1‎-2c) (4)(-2x-y)(2x-y)‎ 例2 、运用平方差公式计算 1998×2002 ‎ 解：1998×2002 =（2000- ）×(2000+ )‎ ‎ =‎ ‎ = ‎ 3‎ 例3 、街心花园有一块边长为a米的正方形草坪，经统一规划后，南北向要加长2米，而东西向要缩短2米，问改造后的长方形草坪的面积是多少？‎ ‎【随堂练习】‎ ‎1.(x+6)(6-x)=________,=_____________.毛 ‎2..‎ ‎3.(x-1)(+1)( )=-1.‎ ‎4.(a+b+c)(a-b-c)=[a+( )][a-( )].‎ ‎5.(a-b-c-d)(a+b-c+d)=[( )+( )][( )-( )]‎ ‎【中考连线】‎ 计算:‎ ‎【参考答案】‎ 随堂练习 ‎1.36-x2,x2- 2.‎-2a2+5b 3.x+1 4.b+c,b+c 5.a-c,b+d,a-c,b+d ‎ 中考连线 原式==.‎ 3‎