河南省洛阳市宜阳县2018-2019学年第一学期期末教学质量检测八年级数学试卷 6页

河南省洛阳市宜阳县2018〜2019学年第一学期期末教学质量检测八年级数学试卷 一、选择题（每小题3分，共30分）‎ ‎1. -9的立方根为 A. 3 B.-3 C. 3 或-3 D. ‎‎3‎‎-9‎ ‎2. 下列各式中，正确的是 （‎ A. 3‎2‎ >2‎3‎ B.a3 • a2=a6 C. (b+2a) (2a —6) =b2 —4a2 D. 5m + 2m = 7m2‎ ‎3. 若 x2 —2x—m= (x+n) (x—3)，则 m + n 的值为 （‎ A. 4 B.8 C. -4 D. 6‎ ‎4. 已知（x+y)2 = 1，（x —y)2=49,则:x y 的值为 （‎ A. 12 B. -12 C. 5 D. -5‎ ‎5. 如图，下列条件中，不能证明ΔABC ‎≅‎ΔDCB的是 （‎ A. AB=DC, AC=DB B. AB=DC，∠ABC=∠DCB C. BO=CO, ∠A = ∠D D.AB=DC, ∠A = ∠D ‎6. 下列各组数中，以它们为边的三角形不是直角三角形的是（ ）‎ A.3,4,5 B.5,12,13 C. 7,24,25 D. 5,7,9‎ ‎7. 如图，在RtΔABC中，∠A = 90°，∠ABC的平分线交AC于点D,AD = 3，BC=10,则ΔBDC 的面积是 （ ）‎ A. 15 B. 12 C. 30 D. 10‎ ‎8. —次跳远比赛中，成绩在4. 05米以上的有8人，频率为0.4,参加比赛的共有 （ ）‎ A. 10 人 B. 20 人 C. 30 人 D. 40 人 ‎9. “赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形，如图，每一个直角三角形的两条直角的长分别是3和4, 则中间的小正方形和大正方形的面积比是 （ ）‎ A. 3 : 4 B. 1 : 25 C.1:5 D. 1 ：10‎ ‎10. 如图，每个小正方形的边长为1，点A、B、C是小正方形的顶点， 则∠ABC的度数为 （ ）‎ A.90° B.60° C. 45° D.30°‎ 二、填空题（每小题3分，共15分}‎ ‎11. 9的平方根为 .‎ ‎12. 计算：（x+5)(x-7)= .‎ ‎13. 如图，在ΔABC中，AB=AD=DC,∠B=70°，则∠C= ‎ ‎14. 在 RtΔABC 中,AB=3 cm，BC=4 cm，则 AC 边的长为_ .‎ ‎15. 如图，在四边形 ABCD 中.AD=4，CD=3，∠ABC=∠ACB =∠ADC= 45°，则 BD 的长为 .‎ 三、解答题（本大题共8个小题，共75分}‎ ‎16. 分解因式：（每小题4分，共8分）‎ ‎(1)x3 —4x2 +4x： (2)(x +1)(x—4) + 3x.‎ ‎17. 求下列各式的值：（每小题7分，共14分）‎ ‎(1)已知 2x2+3x - 5 = 0,求代数式 3x(2x+1) — (2x + 1) (2x- 1)的值；‎ ‎(2)已知a=‎3‎‎2‎‎,b=‎‎4‎‎3‎，求代数式[(ab+1) (ab- 2) — 2a2b2 +2]‎÷‎ (-ab)的值.‎ ‎18. (8 分）如图，已知：∠BDA = ∠CEA，AE = AD.求证：∠ABC = ∠ACB.‎ ‎19. (9分)求证：三角形的三条角平分线交于一点.‎ ‎20. 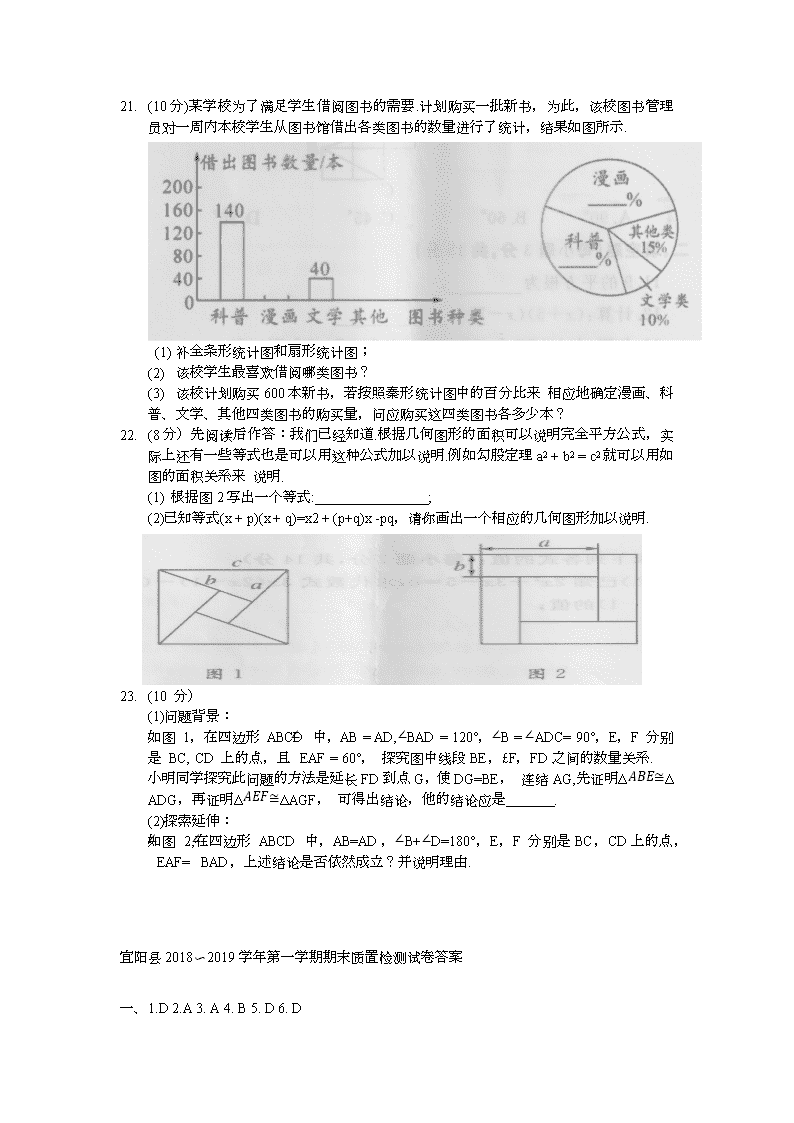(8 分）有一块四边形土地 ABCD(如图），∠B = 90°，AB = 4m，BC =3 m，CD=12 m，DA = 13 m，求该四边形地的面积（8分）‎ ‎21. (10分)某学校为了满足学生借阅图书的需要.计划购买一批新书，为此，该校图书管理员对一周内本校学生从图书馆借出各类图书的数量进行了统计，结果如图所示.‎ ‎ (1) 补全条形统计图和扇形统计图；‎ ‎(2) 该校学生最喜欢借阅哪类图书？‎ ‎(3) 该校计划购买600本新书，若按照秦形统计图中的百分比来 相应地确定漫画、科普、文学、其他四类图书的购买量，问应购买这四类图书各多少本？‎ ‎22. (8分）先阅读后作答：我们已经知道.根据几何图形的面积可以说明完全平方公式，实际上还有一些等式也是可以用这种公式加以说明.例如勾股定理a2 + b2 = c2就可以用如图的面积关系来 说明.‎ ‎(1) 根据图2写出一个等式: ;‎ ‎(2)已知等式(x + p)(x + q)=x2 + (p+q)x -pq，请你画出一个相应的几何图形加以说明.‎ ‎23. (10 分）‎ ‎(1)问题背景：‎ 如图 1，在四边形 ABCD 中，AB = AD,∠BAD = 120°，∠B = ∠ADC= 90°，E，F 分别是 BC, CD 上的点，且∠EAF = 60°， 探究图中线段BE，£F，FD之间的数量关系.‎ 小明同学探究此问题的方法是延长FD到点G，使DG=BE， 连结AG,先证明ΔABE≅‎ΔADG，再证明ΔAEF≅‎ΔAGF， 可得出结论，他的结论应是 .‎ ‎(2)探索延伸：‎ 如图 2,在四边形 ABCD 中，AB=AD，∠B+∠D=180°，E，F 分别是BC，CD上的点，∠EAF=∠BAD，上述结论是否依然成立？并说明理由.‎ 宜阳县2018〜2019学年第一学期期末质置检测试卷答案 一、1.D 2.A 3. A 4. B 5. D 6. D