2019-2020学年河南省洛阳市洛宁县八年级下学期期末数学试卷 （解析版） 22页

‎2019-2020学年河南省洛阳市洛宁县八年级第二学期期末数学试卷 一、选择题 ‎1．使分式有意义的x的取值范围是（　　）‎ A．x＞3 B．x≠‎3 ‎C．x＜3 D．x＝3‎ ‎2．将（）﹣1、（﹣3）0、（﹣4）2这三个数按从小到大的顺序排列，结果正确的是（　　）‎ A．（）﹣1＜（﹣3）0＜（﹣4）2 B．（﹣3）0＜（）﹣1＜（﹣4）2 ‎ C．（﹣4）2＜（）﹣1＜（﹣3）0 D．（﹣3）0＜（﹣4）2＜（）﹣1‎ ‎3．PM2.5是指大气中直径≤‎0.0000025米的颗粒物，将0.0000025用科学记数法表示为（　　）‎ A．2.5×10﹣7 B．2.5×10﹣‎6 ‎C．25×10﹣7 D．0.25×10﹣5‎ ‎4．下表记录了甲、乙、丙、丁四名同学参加某区“中华魂”主题教育演讲比赛的相关数据：根据表中数据，要从中选择一名成绩好且发挥稳定的同学参加市级比赛，应该选择（　　）‎ 甲 乙 丙 丁 平均数（分）‎ ‎90‎ ‎80‎ ‎90‎ ‎80‎ 方差 ‎2.4‎ ‎2.2‎ ‎5.4‎ ‎2.4‎ A．甲 B．乙 C．丙 D．丁 ‎5．已知正比例函数y＝kx（k≠0）的函数值y随x的增大而减小，则一次函数y＝x+k的图象大致是（　　）‎ A． B． ‎ C． D．‎ ‎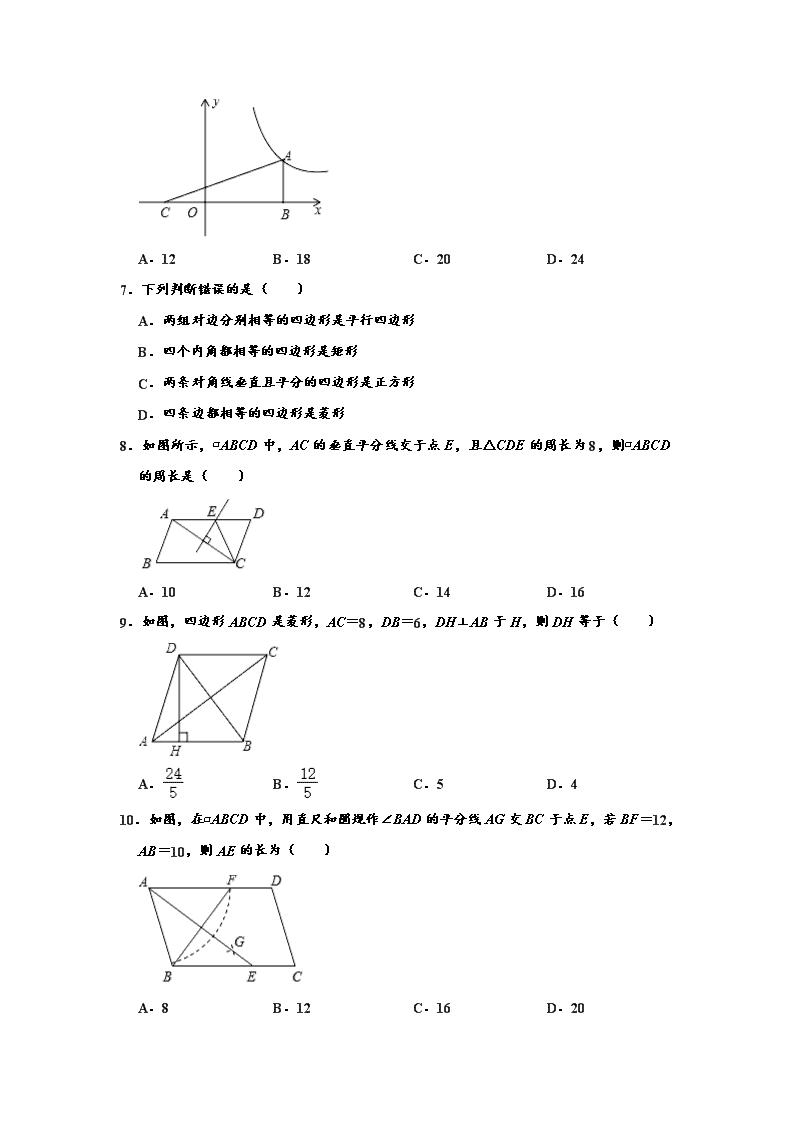6．如图，点A在反比例函数y＝（x＞0，k＞0）的图象上，AB⊥x轴于点B，点C在x轴的负半轴上，且BO＝2CO，若△ABC的面积为18，则k的值为（　　）‎ A．12 B．‎18 ‎C．20 D．24‎ ‎7．下列判断错误的是（　　）‎ A．两组对边分别相等的四边形是平行四边形 ‎ B．四个内角都相等的四边形是矩形 ‎ C．两条对角线垂直且平分的四边形是正方形 ‎ D．四条边都相等的四边形是菱形 ‎8．如图所示，▱ABCD中，AC的垂直平分线交于点E，且△CDE的周长为8，则▱ABCD的周长是（　　）‎ A．10 B．‎12 ‎C．14 D．16‎ ‎9．如图，四边形ABCD是菱形，AC＝8，DB＝6，DH⊥AB于H，则DH等于（　　）‎ A． B． C．5 D．4‎ ‎10．如图，在▱ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E，若BF＝12，AB＝10，则AE的长为（　　）‎ A．8 B．‎12 ‎C．16 D．20‎ 二、填空题（本大题共5小题，共15分）‎ ‎11．计算：+＝　 　．‎ ‎12．在▱ABCD中，∠B+∠D＝200°，则∠A＝　 　．‎ ‎13．已知正比例函数；y＝（‎3m﹣2）x的图象上两点A（x1，y1），B（x2，y2），当x1＜x2时，有y1＞y2，那么m的取值范围是　 　．‎ ‎14．如果一组数据﹣3，﹣2，0，1，x，6，9，12的平均数为3，那么这组数据的中位数是　 　．‎ ‎15．如图所示，正方形ABCD的边长为4，E是边BC上的一点，且BE＝1，P是对角线AC上的一动点，连接PB、PE，当点P在AC上运动时，△PBE周长的最小值是　 　．‎ 三、解答题（本大题共8小题，共75分）‎ ‎16．先化简，再求值：÷（﹣），其中a＝2，b＝3．‎ ‎17．某校初一开展英语拼写大赛，爱国班和求知班根据初赛成绩，各选出5名选手参加复赛，两个班备选出的5名选手的复赛成绩如图所示：‎ 班级 平均数（分）‎ 中位数（分）‎ 众数（分）‎ 爱国班 a ‎85‎ c 求知班 ‎85‎ b ‎100‎ ‎（1）根据图示直接写出a，b，c的值；‎ ‎（2）已知爱国班复赛成绩方差是70，请求出求知班复赛成绩的方差，并说明哪个班成绩比较稳定？‎ ‎18．已知：一次函数y＝kx+b的图象经过M（0，2），N（1，3）两点．‎ ‎（1）求k、b的值；‎ ‎（2）若一次函数y＝kx+b的图象与x轴交点为A（a，0），求a的值．‎ ‎19．如图，在平面直角坐标系中，直线y＝x+b与双曲线y＝相交于A、B两点，已知A （2，5），B（﹣5，m）．求：‎ ‎（1）求一次函数与反比例函数的表达式；‎ ‎（2）△OAB的面积．‎ ‎20．如图所示，O是平行四边形ABCD对角线的交点，过点O的直线EF分别交AD、BC于E、F两点，连结AF、CE，求证：四边形AECF是平行四边形．‎ ‎21．如图，在矩形ABCD中，AE平分∠BAD，∠1＝15°．‎ ‎（1）求∠2的度数；‎ ‎（2）求证：BO＝BE．‎ ‎22．如图，O是矩形ABCD对角线的交点，DE∥AC，CE∥BD，试说明OE与CD互相垂直平分．‎ ‎23．【问题情境】‎ 如图1，四边形ABCD是正方形，M是BC边上的一点，E是CD边的中点，AE平分∠DAM．‎ ‎【探究展示】‎ ‎（1）证明：AM＝AD+MC；‎ ‎（2）AM＝DE+BM是否成立？若成立，请给出证明；若不成立，请说明理由．‎ ‎【拓展延伸】‎ ‎（3）若四边形ABCD是长与宽不相等的矩形，其他条件不变，如图2，探究展示（1）、（2）中的结论是否成立？请分别作出判断，不需要证明．‎ 参考答案 一、选择题（本大题共10小题，共30分）‎ ‎1．使分式有意义的x的取值范围是（　　）‎ A．x＞3 B．x≠‎3 ‎C．x＜3 D．x＝3‎ ‎【分析】直接利用分式有意义则其分母不为零，进而得出答案．‎ 解：∵使分式有意义，‎ ‎∴x﹣3≠0，‎ 解得：x≠3．‎ 故选：B．‎ ‎2．将（）﹣1、（﹣3）0、（﹣4）2这三个数按从小到大的顺序排列，结果正确的是（　　）‎ A．（）﹣1＜（﹣3）0＜（﹣4）2 B．（﹣3）0＜（）﹣1＜（﹣4）2 ‎ C．（﹣4）2＜（）﹣1＜（﹣3）0 D．（﹣3）0＜（﹣4）2＜（）﹣1‎ ‎【分析】先计算出各数的值，然后按有理数大小的比较法则进行判断．‎ 解：（）﹣1＝5，（﹣3）0＝1，（﹣4）2＝16；‎ ‎∵1＜5＜16，∴（﹣3）0＜（）﹣1＜（﹣4）2．‎ 故选：B．‎ ‎3．PM2.5是指大气中直径≤‎0.0000025米的颗粒物，将0.0000025用科学记数法表示为（　　）‎ A．2.5×10﹣7 B．2.5×10﹣‎6 ‎C．25×10﹣7 D．0.25×10﹣5‎ ‎【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．‎ 解：0.0000025＝2.5×10﹣6，‎ 故选：B．‎ ‎4．下表记录了甲、乙、丙、丁四名同学参加某区“中华魂”‎ 主题教育演讲比赛的相关数据：根据表中数据，要从中选择一名成绩好且发挥稳定的同学参加市级比赛，应该选择（　　）‎ 甲 乙 丙 丁 平均数（分）‎ ‎90‎ ‎80‎ ‎90‎ ‎80‎ 方差 ‎2.4‎ ‎2.2‎ ‎5.4‎ ‎2.4‎ A．甲 B．乙 C．丙 D．丁 ‎【分析】根据平均数和方差的意义解答．‎ 解：从平均数看，成绩最好的是甲、丙同学，‎ 从方差看，甲、丁方差小，发挥最稳定，‎ 所以要从中选择一名成绩好且发挥稳定的同学参加市级比赛，应该选择甲，‎ 故选：A．‎ ‎5．已知正比例函数y＝kx（k≠0）的函数值y随x的增大而减小，则一次函数y＝x+k的图象大致是（　　）‎ A． B． ‎ C． D．‎ ‎【分析】根据自正比例函数的性质得到k＜0，然后根据一次函数的性质得到一次函数y＝x+k的图象经过第一、三象限，且与y轴的负半轴相交．‎ 解：∵正比例函数y＝kx（k≠0）的函数值y随x的增大而减小，‎ ‎∴k＜0，‎ ‎∵一次函数y＝x+k的一次项系数大于0，常数项小于0，‎ ‎∴一次函数y＝x+k的图象经过第一、三象限，且与y轴的负半轴相交．‎ 故选：B．‎ ‎6．如图，点A在反比例函数y＝（x＞0，k＞0）的图象上，AB⊥x轴于点B，点C在x轴的负半轴上，且BO＝2CO，若△ABC的面积为18，则k的值为（　　）‎ A．12 B．‎18 ‎C．20 D．24‎ ‎【分析】设出A点的坐标，从而表示出线段CB，AB的长，根据三角形的面积为18，构建方程即可求出k的值．‎ 解：设A点的坐标为，‎ 则OB＝a，AB＝，‎ ‎∵BO＝2CO，‎ ‎∴CB＝，‎ ‎∴△ABC的面积为：＝18，‎ 解得k＝24，‎ 故选：D．‎ ‎7．下列判断错误的是（　　）‎ A．两组对边分别相等的四边形是平行四边形 ‎ B．四个内角都相等的四边形是矩形 ‎ C．两条对角线垂直且平分的四边形是正方形 ‎ D．四条边都相等的四边形是菱形 ‎【分析】根据平行四边形、菱形、正方形以及矩形的判定定理进行判断．‎ 解：A、两组对边分别相等的四边形是平行四边形，故本选项正确；‎ B、四个内角都相等的四边形是矩形，故本选项正确；‎ C、两条对角线垂直且平分的四边形是菱形，不一定是正方形，故本选项错误；‎ D、四条边都相等的四边形是菱形，故本选项正确．‎ 故选：C．‎ ‎8．如图所示，▱ABCD中，AC的垂直平分线交于点E，且△CDE的周长为8，则▱ABCD的周长是（　　）‎ A．10 B．‎12 ‎C．14 D．16‎ ‎【分析】根据线段垂直平分线的性质，可得AE＝CE，即可得△CDE的周长等于AD+CD，进而解答即可．‎ 解：∵AC的垂直平分线交于点E，‎ ‎∴AE＝CE，‎ ‎∵△CDE的周长＝CD+DE+CE＝CD+DE+AE＝CD+AD＝8，‎ ‎∴▱ABCD的周长＝2（CD+AD）＝16，‎ 故选：D．‎ ‎9．如图，四边形ABCD是菱形，AC＝8，DB＝6，DH⊥AB于H，则DH等于（　　）‎ A． B． C．5 D．4‎ ‎【分析】根据菱形性质求出AO＝4，OB＝3，∠AOB＝90°，根据勾股定理求出AB，再根据菱形的面积公式求出即可．‎ 解：∵四边形ABCD是菱形，‎ ‎∴AO＝OC，BO＝OD，AC⊥BD，‎ ‎∵AC＝8，DB＝6，‎ ‎∴AO＝4，OB＝3，∠AOB＝90°，‎ 由勾股定理得：AB＝＝5，‎ ‎∵S菱形ABCD＝，‎ ‎∴，‎ ‎∴DH＝，‎ 故选：A．‎ ‎10．如图，在▱ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E，若BF＝12，AB＝10，则AE的长为（　　）‎ A．8 B．‎12 ‎C．16 D．20‎ ‎【分析】由基本作图得到AB＝AF，加上AO平分∠BAD，则根据等腰三角形的性质得到AO⊥BF，BO＝FO＝BF＝6，再根据平行四边形的性质得AF∥BE，所以∠1＝∠3，于是得到∠2＝∠3，根据等腰三角形的判定得AB＝EB，然后再根据等腰三角形的性质得到AO＝OE，最后利用勾股定理计算出AO，从而得到AE的长．‎ 解：连结EF，AE与BF交于点O，如图，‎ ‎∵AB＝AF，AO平分∠BAD，‎ ‎∴AO⊥BF，BO＝FO＝BF＝6，‎ ‎∵四边形ABCD为平行四边形，‎ ‎∴AF∥BE，‎ ‎∴∠1＝∠3，‎ ‎∴∠2＝∠3，‎ ‎∴AB＝EB，‎ 而BO⊥AE，‎ ‎∴AO＝OE，‎ 在Rt△AOB中，AO＝＝8，‎ ‎∴AE＝2AO＝16．‎ 故选：C．‎ 二、填空题（本大题共5小题，共15分）‎ ‎11．计算：+＝　1　．‎ ‎【分析】根据同分母分式相加，分母不变分子相加，可得答案．‎ 解：原式＝＝1，‎ 故答案为：1．‎ ‎12．在▱ABCD中，∠B+∠D＝200°，则∠A＝　80°　．‎ ‎【分析】根据平行四边形的对角相等、邻角互补即可得出∠A的度数．‎ 解：如图所示：‎ ‎∵四边形ABCD是平行四边形，‎ ‎∴AD∥BC，∠B＝∠D，‎ ‎∴∠A+∠B＝180°，‎ ‎∵∠B+∠D＝200°，‎ ‎∴∠B＝∠D＝100°，‎ ‎∴∠A＝180°﹣∠B＝180°﹣100°＝80°．‎ 故答案为：80°．‎ ‎13．已知正比例函数；y＝（‎3m﹣2）x的图象上两点A（x1，y1），B（x2，y2），当x1＜x2时，有y1＞y2，那么m的取值范围是　m＜　．‎ ‎【分析】由当x1＜x2时，有y1＞y2，可得出y随x的增大而减小，结合一次函数的性质可得出‎3m﹣2＜0，解之即可得出m的取值范围．‎ 解：∵当x1＜x2时，有y1＞y2，‎ ‎∴y随x的增大而减小，‎ ‎∴‎3m﹣2＜0，‎ 解得：m＜．‎ 故答案为：m＜．‎ ‎14．如果一组数据﹣3，﹣2，0，1，x，6，9，12的平均数为3，那么这组数据的中位数是　1　．‎ ‎【分析】本题可结合平均数的定义先算出x的值，再把数据按从小到大的顺序排列，找出最中间的数，即为中位数．‎ 解：数据﹣3，﹣2，0，1，x，6，9，12的平均数为3，‎ 即有（﹣3﹣2+0+1+x+6+9+12）＝3，求得x＝1．‎ 将这组数据从小到大重新排列后为﹣3，﹣2，0，1，1，6，9，12；‎ 这组数据的中位数是＝1．‎ 故填1．‎ ‎15．如图所示，正方形ABCD的边长为4，E是边BC上的一点，且BE＝1，P是对角线AC上的一动点，连接PB、PE，当点P在AC上运动时，△PBE周长的最小值是　6　．‎ ‎【分析】根据两点之间线段最短和点B和点D关于AC对称，即可求得△PBE周长的最小值，本题得以解决．‎ 解：连接DE于AC交于点P′，连接BP′，则此时△BP′E的周长就是△PBE周长的最小值，‎ ‎∵BE＝1，BC＝CD＝4，‎ ‎∴CE＝3，DE＝5，‎ ‎∴BP′+P′E＝DE＝5，‎ ‎∴△PBE周长的最小值是5+1＝6，‎ 故答案为：6．‎ 三、解答题（本大题共8小题，共75分）‎ ‎16．先化简，再求值：÷（﹣），其中a＝2，b＝3．‎ ‎【分析】先根据分式混合运算顺序和运算法则化简原式，再将a、b的值代入计算可得．‎ 解：原式＝÷（﹣）‎ ‎＝•‎ ‎＝，‎ 当a＝2，b＝3时，原式＝＝3．‎ ‎17．某校初一开展英语拼写大赛，爱国班和求知班根据初赛成绩，各选出5名选手参加复赛，两个班备选出的5名选手的复赛成绩如图所示：‎ 班级 平均数（分）‎ 中位数（分）‎ 众数（分）‎ 爱国班 a ‎85‎ c 求知班 ‎85‎ b ‎100‎ ‎（1）根据图示直接写出a，b，c的值；‎ ‎（2）已知爱国班复赛成绩方差是70，请求出求知班复赛成绩的方差，并说明哪个班成绩比较稳定？‎ ‎【分析】（1）直接根据方差、中位数和众数的定义求解可得；‎ ‎（2）根据方差的定义求出求知班成绩的方差，再利用方差的意义求解可得．‎ 解：（1）由条形统计图知，a＝＝85；c＝85；‎ 求知班的5位选手的成绩从小到大排列为：70、75、80、100、100，‎ 所以b＝80；‎ ‎（2）求知班成绩的方差为×[（70﹣85）2+（75﹣85）2+（80﹣85）2+2×（100﹣85）2]＝160，‎ ‎∵70＜160，‎ ‎∴爱国班的成绩比较稳定．‎ ‎18．已知：一次函数y＝kx+b的图象经过M（0，2），N（1，3）两点．‎ ‎（1）求k、b的值；‎ ‎（2）若一次函数y＝kx+b的图象与x轴交点为A（a，0），求a的值．‎ ‎【分析】（1）根据待定系数法求出一次函数解析式即可；‎ ‎（2）根据图象与函数坐标轴交点坐标求法得出a的值．‎ 解：（1）由题意得，‎ 解得．‎ ‎∴k，b的值分别是1和2；‎ ‎（2）将k＝1，b＝2代入y＝kx+b中得y＝x+2．‎ ‎∵点A（a，0）在 y＝x+2的图象上，‎ ‎∴0＝a+2，‎ 即a＝﹣2．‎ ‎19．如图，在平面直角坐标系中，直线y＝x+b与双曲线y＝相交于A、B两点，已知A （2，5），B（﹣5，m）．求：‎ ‎（1）求一次函数与反比例函数的表达式；‎ ‎（2）△OAB的面积．‎ ‎【分析】（1）把A （2，5）代入双曲线y＝可确定反比例函数的关系式，进而求点B坐标，再根据待定系数法求出一次函数的关系式；‎ ‎（2）求出一次函数与y轴的交点坐标，进而将S△AOB转化为S△BOC+S△AOC利用坐标转化为底或高计算即可．‎ 解：把A （2，5）代入双曲线y＝得，k＝2×5＝10，‎ ‎∴反比例函数的关系式为y＝，‎ 把B（﹣5，m）代入为y＝得，m＝＝﹣2，‎ ‎∴B（﹣5，﹣2），‎ 把A （2，5）、B（﹣5，﹣2）代入y＝x+b得，‎ ‎，‎ 解得，，‎ ‎∴一次函数的关系式为y＝x+3，‎ 当x＝0时，y＝3，即C（0，3），‎ ‎∴OC＝3，‎ ‎∴S△AOB＝S△BOC+S△AOC＝×3×5+×3×2＝，‎ ‎20．如图所示，O是平行四边形ABCD对角线的交点，过点O的直线EF分别交AD、BC于E、F两点，连结AF、CE，求证：四边形AECF是平行四边形．‎ ‎【分析】首先证明BO＝DO，∠EDO＝∠FBO，然后在证明△DEO≌△FBO进而得到EO＝FO，再根据对角线互相平分的四边形是平行四边形可得结论．‎ ‎【解答】证明：∵四边形ABCD为平行四边形，‎ ‎∴AD∥BC，‎ ‎∴∠EDO＝∠FBO，‎ ‎∵O是平行四边形ABCD对角线的交点，‎ ‎∴BO＝DO，‎ 在△DEO和△FBO中，‎ ‎∴△DEO≌△BFO（ASA），‎ ‎∴DE＝BF，‎ ‎∵在▱ABCD中，DA＝BC，‎ ‎∴DA﹣DE＝BC﹣BF，‎ ‎∴AE＝CF，‎ ‎∵AE＝CF且AE∥CF，‎ ‎∴四边形AECF为平行四边形．‎ ‎21．如图，在矩形ABCD中，AE平分∠BAD，∠1＝15°．‎ ‎（1）求∠2的度数；‎ ‎（2）求证：BO＝BE．‎ ‎【分析】（1）利用矩形的性质和角平分线的性质可知∠AEB＝∠EAD＝45°，则∠2＝∠AEB﹣∠1＝30°；‎ ‎（2）通过∠2＝30°，∠BAO＝60°证得△AOB为等边三角形，结合AB＝BE可得BO＝BE．‎ ‎【解答】（1）解：∵在矩形ABCD中，AE平分∠BAD，∠1＝15°，‎ ‎∴∠AEB＝∠EAD＝45°．‎ ‎∴∠2＝∠AEB﹣∠1＝30°．‎ ‎（2）证明：由（1）可知∠2＝30°，‎ ‎∴∠BAO＝60°．‎ ‎∵OA＝OB，‎ ‎∴△OAB是等边三角形．‎ ‎∴OB＝AB，‎ ‎∵∠AEB＝∠EAD＝∠BAE＝45°，‎ ‎∴AB＝BE．‎ ‎∴BO＝BE．‎ ‎22．如图，O是矩形ABCD对角线的交点，DE∥AC，CE∥BD，试说明OE与CD互相垂直平分．‎ ‎【分析】已知OE与CD是四边形OCDE的对角线，且DE∥AC，CE∥BD，即：四边形OCED是平行四边形，要证明OE⊥CD，只需证明四边形OCED是菱形，由菱形的对角线互相垂直即可求解．‎ ‎【解答】证明：∵四边形ABCD是矩形，‎ ‎∴AC＝BD，OA＝OC＝OD＝OB（矩形的对角线相等且互相平分），‎ 又∵DE∥AC，CE∥BD，‎ ‎∴四边形OCED是平行四边形，‎ 又∵OC＝OD，‎ ‎∴四边形OCED是菱形，‎ ‎∴OE⊥CD且OE与CD互相平分（菱形的对角线互相垂直平分）．‎ ‎23．【问题情境】‎ 如图1，四边形ABCD是正方形，M是BC边上的一点，E是CD边的中点，AE平分∠DAM．‎ ‎【探究展示】‎ ‎（1）证明：AM＝AD+MC；‎ ‎（2）AM＝DE+BM是否成立？若成立，请给出证明；若不成立，请说明理由．‎ ‎【拓展延伸】‎ ‎（3）若四边形ABCD是长与宽不相等的矩形，其他条件不变，如图2，探究展示（1）、（2）中的结论是否成立？请分别作出判断，不需要证明．‎ ‎【分析】（1）延长AE、BC交于点N，易证△ADE≌△NCE，从而有AD＝CN ‎，只需证明AM＝NM即可．‎ ‎（2）作FA⊥AE交CB的延长线于点F，易证AM＝FM，只需证明FB＝DE即可；要证FB＝DE，只需证明它们所在的两个三角形全等即可．‎ ‎（3）在图2（1）中，仿照（1）中的证明思路即可证到AM＝AD+MC仍然成立；在图2（2）中，采用反证法，并仿照（2）中的证明思路即可证到AM＝DE+BM不成立．‎ ‎【解答】（1）证明：延长AE、BC交于点N，如图1（1），‎ ‎∵四边形ABCD是正方形，‎ ‎∴AD∥BC．‎ ‎∴∠DAE＝∠CNE．‎ ‎∵AE平分∠DAM，‎ ‎∴∠DAE＝∠MAE．‎ ‎∴∠CNE＝∠MAE．‎ ‎∴AM＝MN．‎ ‎∵E是CD边的中点，‎ ‎∴DE＝CE，‎ 在△ADE和△NCE中，，‎ ‎∴△ADE≌△NCE（AAS）‎ ‎∴AD＝NC．‎ ‎∴AM＝MN＝NC+MC＝AD+MC．‎ ‎（2）解：AM＝DE+BM成立，理由如下：‎ 如图1（2）所示：‎ ‎∵四边形ABCD是正方形，‎ ‎∴∠BAD＝∠D＝∠ABC＝90°，AB＝AD，AB∥DC．‎ ‎∴∠ABF＝90°＝∠D，‎ ‎∵AF⊥AE，‎ ‎∴∠FAE＝90°，‎ ‎∴∠BAF＝90°﹣∠BAE＝∠DAE，‎ 在△ABF和△ADE中，，‎ ‎∴△ABF≌△ADE（ASA），‎ ‎∴BF＝DE，∠F＝∠AED，‎ ‎∵AB∥DC，‎ ‎∴∠AED＝∠BAE，‎ ‎∵∠FAB＝∠EAD＝∠EAM，‎ ‎∴∠AED＝∠BAE＝∠BAM+∠EAM＝∠BAM+∠FAB＝∠FAM，‎ ‎∴∠F＝∠FAM．‎ ‎∴AM＝FM，‎ ‎∴AM＝FB+BM＝DE+BM；‎ ‎（3）解：（1）结论AM＝AD+MC仍然成立，理由如下：‎ 延长AE、BC交于点P，如图2（1），‎ ‎∵四边形ABCD是矩形，‎ ‎∴AD∥BC，‎ ‎∴∠DAE＝∠P，‎ ‎∵AE平分∠DAM，‎ ‎∴∠DAE＝∠MAE，‎ ‎∴∠P＝∠MAE，‎ ‎∴MA＝MP，‎ 在△ADE和△PCE中，，‎ ‎∴△ADE≌△PCE（AAS），‎ ‎∴AD＝PC．‎ ‎∴MA＝MP＝PC+MC＝AD+MC．‎ ‎（2）结论AM＝DE+BM不成立．理由如下：‎ 假设AM＝DE+BM成立．过点A作AQ⊥AE，交CB的延长线于点Q，如图2（2）所示．‎ ‎∵四边形ABCD是矩形，‎ ‎∴∠BAD＝∠D＝∠ABC＝90°，AB∥DC．‎ ‎∵AQ⊥AE，‎ ‎∴∠QAE＝90°．‎ ‎∴∠BAQ＝90°﹣∠BAE＝∠DAE．‎ ‎∴∠Q＝90°﹣∠BAQ＝90°﹣∠DAE＝∠AED．‎ ‎∵AB∥DC，‎ ‎∴∠AED＝∠BAE．‎ ‎∵∠BAQ＝∠EAD＝∠EAM，‎ ‎∴∠AED＝∠BAE＝∠BAM+∠EAM＝∠BAM+∠BAQ，‎ ‎∴∠Q＝∠QAM．‎ ‎∴AM＝QM．‎ ‎∴AM＝BQ+BM．‎ ‎∵AM＝DE+BM，‎ ‎∴BQ＝DE．‎ 在△ABQ和△ADE中，‎ ‎∴△ABQ≌△ADE（AAS），‎ ‎∴AB＝AD．与条件“AB≠AD“矛盾，故假设不成立．‎ ‎∴AM＝DE+BM不成立．‎