人教版八年级数学上册第十二章测试题及答案 10页

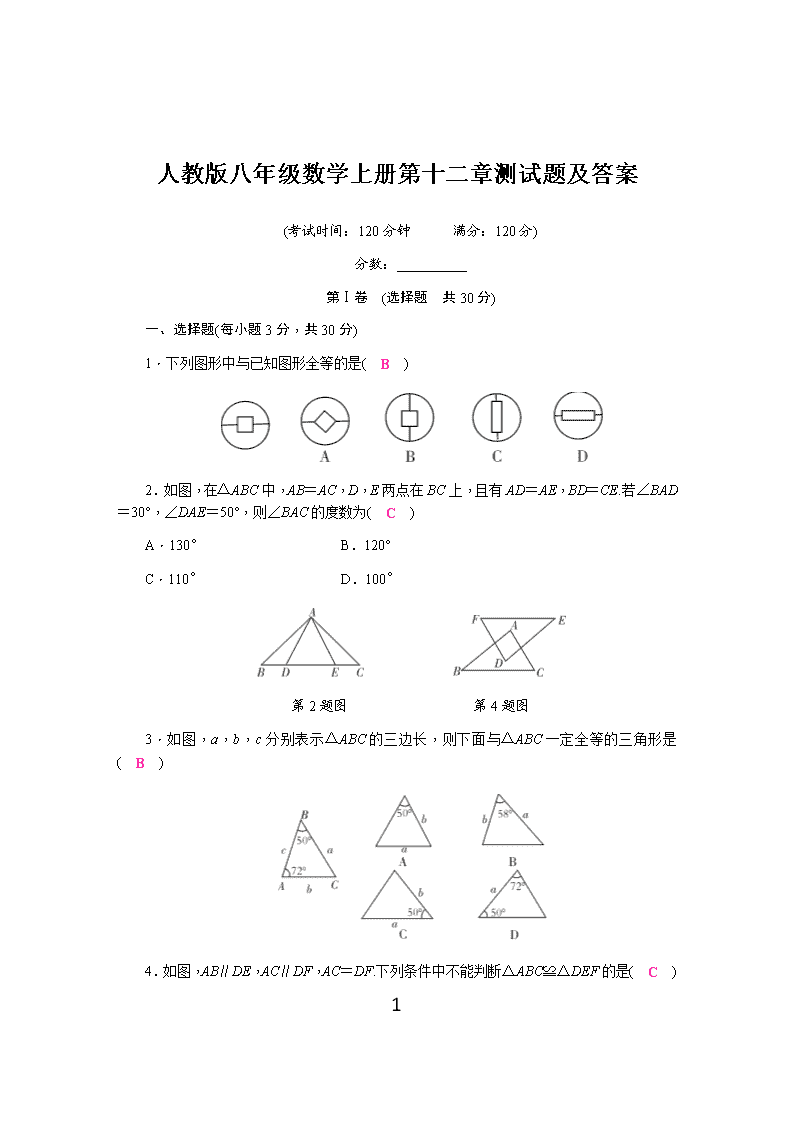
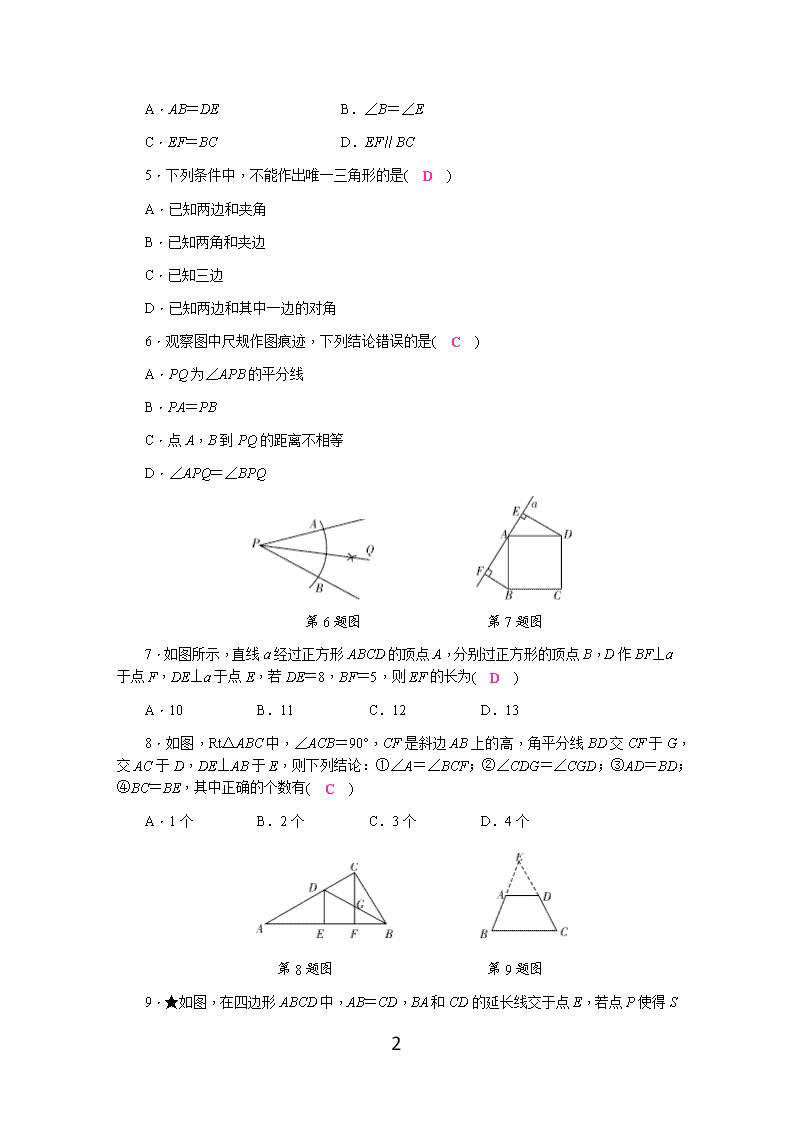
‎ ‎ 人教版八年级数学上册第十二章测试题及答案 ‎(考试时间：120分钟　　　满分：120分)‎ 分数：__________‎ 1‎ 第Ⅰ卷　(选择题　共30分)‎ 一、选择题(每小题3分，共30分)‎ ‎1．下列图形中与已知图形全等的是(　B　)‎ ‎2．如图，在△ABC中，AB＝AC，D，E两点在BC上，且有AD＝AE，BD＝CE.若∠BAD＝30°，∠DAE＝50°，则∠BAC的度数为(　C　)‎ A．130°　　　　　　　　　 B．120°‎ C．110° D．100°‎ ‎ ‎ 第2题图　　 　第4题图 ‎3．如图，a，b，c分别表示△ABC的三边长，则下面与△ABC一定全等的三角形是(　B　)‎ ‎4．如图，AB∥DE，AC∥DF，AC＝DF.下列条件中不能判断△ABC≌△DEF的是(　C　)‎ 10‎ A．AB＝DE B．∠B＝∠E C．EF＝BC D．EF∥BC ‎5．下列条件中，不能作出唯一三角形的是(　D　)‎ A．已知两边和夹角 B．已知两角和夹边 C．已知三边 D．已知两边和其中一边的对角 ‎6．观察图中尺规作图痕迹，下列结论错误的是(　C　)‎ A．PQ为∠APB的平分线 B．PA＝PB C．点A，B到PQ的距离不相等 D．∠APQ＝∠BPQ ‎ ‎ 第6题图　　 　第7题图 ‎7．如图所示，直线a经过正方形ABCD的顶点A，分别过正方形的顶点B，D作BF⊥a于点F，DE⊥a于点E，若DE＝8，BF＝5，则EF的长为(　D　)‎ A．10　　　 B．11　　　 C．12　　　 D．13‎ ‎8．如图，Rt△ABC中，∠ACB＝90°，CF是斜边AB上的高，角平分线BD交CF于G，交AC于D，DE⊥AB于E，则下列结论：①∠A＝∠BCF；②∠CDG＝∠CGD；③AD＝BD；④BC＝BE，其中正确的个数有(　C　)‎ A．1个 B．2个 C．3个 D．4个 ‎ ‎ 第8题图　　　 　第9题图 ‎9．★如图，在四边形ABCD中，AB＝CD，BA和CD的延长线交于点E，若点P使得S 10‎ ‎△PAB＝S△PCD，则满足此条件的点P(　D　)‎ A．有且只有1个 B．有且只有2个 C．组成∠E的平分线 D．组成∠E的角平分线和外角平分线所在的直线(E点除外)‎ ‎10．★如图，在长方形ABCD中，AB＝4，AD＝6.延长BC到E，使CE＝2，连接DE，动点P从点B出发，以每秒2个单位的速度沿BC—CD—DA向终点A运动，设点P的运动时间为t秒，当△ABP和△DCE全等时，t的值为(　C　)‎ A．1 B．1或3 C．1或7 D．3或7‎ ‎　 ‎ 第10题图　　 第12题图 第Ⅱ卷　(非选择题　共90分)‎ 二、填空题(每小题3分，共24分)‎ ‎11．在Rt△ABC中，D，E分别是AC，BC上的点，若△ADB≌△EDB≌△EDC，则∠C的度数是 30° .‎ ‎12．如图，已知∠C＝∠D，∠ABC＝∠BAD，AC与BD相交于点O，请写出图中一组相等的线段：__AD＝BC(或OA＝OB或OC＝OD)__ .‎ ‎13．如图，点B，A，D，E在同一直线上，BD＝AE，BC∥EF，要使△ABC≌△DEF，则只需要添加一个适当的条件是 BC＝EF(或∠BAC＝∠EDF或∠C＝∠F或AC∥DF等) ．‎ ‎ ‎ 第13题图　　 　第14题图 ‎14．如图所示，A，B，C，D是四个村庄，B，D，C在一条东西走向公路的沿线上，BD＝1 km，DC＝1 km，村庄A，C和A，D间也有公路相连，且公路AD是南北走向，AC＝3 km，只有AB之间由于间隔了一个小湖，所以无直接相连的公路．现决定在湖面上造一座斜拉桥，测得AE＝1.2 km，BF＝0.7 km，则建造的斜拉桥长至少有 1.1 km. ‎ ‎15．如图所示，△ABC的角平分线AD将BC边分成2∶1两部分，若AC＝3 cm，则AB 10‎ ‎＝ 6cm .‎ ‎ ‎ 第15题图　 第16题图 ‎16．★如图，MN∥PQ，AB⊥PQ，点A，D，B，C分别在直线MN与PQ上，点E在AB上，AD＋BC＝7，AD＝EB，DE＝EC，则AB＝ 7 .‎ ‎17．★如图，在边长为3 cm的正方形ABCD中，点E为BC边上的任意一点，AF⊥AE，交CD的延长线于F，则四边形AFCE的面积为 9 cm2. ‎ ‎ ‎ 第17题图　　　 第18题图 ‎18．★如图，AD是△ABC的中线，E，E分别是AD和AD延长线上的点，且DE＝DF，连接BF，CE.下列说法：①CE＝BF；②△ABD和△ACD的面积相等；③BF∥CE；④△BDF≌△CDE.其中正确的有 ①②③④ (填写正确的序号)．‎ 选择、填空题答题卡 一、选择题(每小题3分，共30分)‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 得分 答案 B C B C D 题号 ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 C D C D C 二、填空题(每小题3分，共24分)得分：______‎ ‎11． 30° 　　12.__AD＝BC(或OA＝OB或OC＝OD)__　13. BC＝EF(或∠BAC＝∠EDF或∠C＝∠F或AC∥DF等) ‎ ‎ 14. 1.1 　15. 6cm 　16. 7 ‎ ‎17． 9 　18. ①②③④ ‎ 10‎ 三、解答题(共66分)‎ ‎19．(8分)如图，工人师傅要检查人字梁的∠B和∠C是否相等，但他手边没有量角器，只有一把刻度尺，他是这样操作的：‎ ‎(1)分别在BA，CA上取BE＝CG；‎ ‎(2)在BC上取BD＝CF；‎ ‎(3)量出DE的长为a米，FG的长为b米，如果a＝b，则说明∠B和∠C是相等的，他的这种做法合理吗？为什么？‎ 解：合理．理由：‎ 由已知条件得在△BED和△CGF中 ‎∴△BED≌△CGF(SSS)，‎ ‎∴∠B＝∠C.‎ ‎20．(8分)你一定玩过跷跷板吧！如图是小明和小刚玩跷跷板的示意图，横板绕它的中点O上下转动，立柱OC与地面垂直，当一方着地时，另一方上升到最高点．问：在上下转动横板的过程中，两人上升的最大高度AA′，BB′有何数量关系，为什么 ?‎ 解：数量关系：‎ AA′＝BB′.‎ 理由如下：∵O是AB′，‎ A′B的中点．‎ ‎∴OA＝OB′，OA′＝OB，‎ 在△A′OA与△BOB′中， 10‎ ‎∴△A′OA≌△BOB′(SAS)，‎ ‎∴AA′＝BB′.‎ ‎21．(8分)如图，A，B两建筑物位于河的两岸，要测它们之间的距离，可以从B点出发在河岸上画一条射线BF，在BF上截取BC＝CD，过D点作DE∥AB，使E，C，A在同一直线上，则DE的长就是A，B之间的距离，请你说明理由．‎ 解：∵DE∥AB，‎ ‎∴∠A＝∠E.‎ ‎∵E，C，A在同一直线上，‎ B，C，D在同一直线上，‎ ‎∴∠ACB＝∠ECD.‎ 在△ABC与△EDC中，‎ ‎∴△ABC≌△EDC(AAS)，‎ ‎∴AB＝DE.‎ ‎22．(10分)如图，△ABC中，AO平分∠BAC，BO平分∠ABC，作OD⊥AB于D，连接CO.‎ 10‎ ‎(1)求证：CO平分∠ACB；‎ ‎(2)当AB＝7，BC＝8，AC＝9时，求AD的长．‎ ‎(1)证明：作OE⊥BC于E，OF⊥AC于F.‎ ‎∵AO平分∠BAC，‎ OD⊥AB，OF⊥AC，‎ ‎∴OD＝OF.‎ ‎∵BO平分∠ABC，OD⊥BA，OE⊥BC，‎ ‎∴OD＝OE，∴OE＝OF，∴CO平分∠ACB.‎ ‎(2)解：易证△AOD≌△AOF，‎ ‎△BOD≌△BOE，△COE≌△COF，‎ ‎∴AD＝AF，BD＝BE，CE＝CF.‎ 设AD＝AF＝x，则BD＝BE＝7－x，‎ CE＝CF＝9－x，‎ ‎∴7－x＋9－x＝8，‎ ‎∴x＝4，‎ ‎∴AD＝4.‎ ‎23．(10分)如图，AB∥CD，以点A为圆心，小于AC的长为半径作圆弧，分别交AB，AC于E，F两点，再分别以E，F为圆心，大于EF长为半径作圆弧，两条圆弧交于点P，作射线AP，交CD于点M.‎ ‎(1)若∠ACD＝114°，求∠MAB的度数；‎ ‎(2)若CN⊥AM，垂足为N.‎ 求证：△ACN≌△MCN.‎ 10‎ ‎(1)解：∵AB∥CD，‎ ‎∴∠ACD＋∠CAB＝180°.‎ ‎∵∠ACD＝114°，‎ ‎∴∠CAB＝66°.‎ 由作法知，AM是∠CAB的平分线，‎ ‎∴∠MAB＝∠CAB＝33°.‎ ‎(2)证明：∵AM平分∠CAB，‎ ‎∴∠CAM＝∠MAB，‎ ‎∵AB∥CD，∴∠MAB＝∠CMA，‎ ‎∴∠CAN＝∠CMN.‎ ‎∵CN⊥AM，∴∠ANC＝∠MNC＝90°，‎ 在△ACN和△MCN中， ‎∴△ACN≌△MCN(AAS)．‎ ‎24．(10分)如图，D为△ABC的边BC上的一点，E为AD上一点，已知∠1＝∠2，∠3＝∠4，求证：AD⊥BC.‎ 证明：在△ABE和△ACE中，‎ ‎∴△ABE≌△ACE(AAS)，‎ 10‎ ‎∴AB＝AC.‎ ‎∵在△ABD和△ACD中，‎ ‎∴△ABD≌△ACD(SAS)，‎ ‎∴∠ADB＝∠ADC.‎ ‎∵∠ADB＋∠ADC＝180°，‎ ‎∴∠ADB＝90°，‎ ‎∴AD⊥BC.‎ ‎25．(12分)如图，在△OAB和△OCD中，OA＝OB，OC＝OD，∠AOB＝∠COD＝α，AC，BD相交于点M.‎ ‎(1)如图①，当α＝90°时，∠AMD的度数为 90° ；‎ ‎(2)如图②，当α＝60°时，∠AMD的度数为 120° ；‎ ‎(3)如图③，当△OCD绕O点任意旋转时，∠AMD与α是否存在着某种确定的数量关系？如果存在，请你用含α的式子表示∠AMD，并用图③进行证明；若不确定，请说明理由．‎ 解：∠AMD＝180°－α.理由如下：‎ 设OB交AC于点K，‎ ‎∵OA＝OB，OC＝OD，‎ ‎∠AOB＝∠COD＝α，‎ ‎∴∠AOC＝∠BOD，‎ ‎∴△AOC≌△BOD(SAS)，‎ 10‎ ‎∴∠OAC＝∠OBD.‎ ‎∵∠AKO＝∠BKM，‎ ‎∴∠AOK＝∠BMK＝α，‎ ‎∴∠AMD＝180°－α.‎ 10‎