线段、角是轴对称图形(2)学案1 3页

‎ ‎ 总 课 题 第一章 轴对称图形 总 课 时 课 题 ‎§1.4 线段、角的轴对称性(2)‎ 课型 新授 教学目标 使学生掌握角是轴对称图形，角平分线的性质。 ‎ 使学生通过类比的思想和方法掌握本节课的内容，培养学生主动探索学习的能力。‎ 通过让学生在原有的知识基础上，通过类比方法，掌握了新的知识，可以提高学生自学的兴趣和信心。‎ 教学重点 角平分线的性质 教学难点 角平分线的性质应用 教具准备 投影仪 教学过程 教 学 内 容 教师活动内容、方式 学生活动方式 设计意图 ‎（一）创设问题情境 张庄、李庄和马庄的位置如图，每两个村庄之间都有笔直的道路相连，他们计划共同打一眼机井。希望机井到三条道路的距离相等，你能设计出机井的位置吗？ ‎ 通过本课的学习，我相信大家将不难解决这个问题。‎ 今天，我们来学习角的轴对称性。‎ ‎（二）新授 ‎1、请同学们将事先准备的薄纸拿出来，在上面任意画一个角（∠AOB），折纸使两边OA、OB重合，你发现折痕与∠AOB有什么关系？‎ 学生通过动手和讨论得到结论：‎ 角是轴对称图形，对称轴是角平分线所在的直线。‎ ‎2、在∠AOB的内部任意取折痕上的一点P，分别作点P到OA和OB的垂线段PC=PD，再沿原折痕折纸，会有什么结论？‎ 学生作图探究，可得到很多结论，如PC=PD，PC、PD关于折痕对称等等，老师点评学生的各种结论并强调重点：角平分线上的点到角的两边距离相等。‎ 由学生自己先做(或互相讨论)，然后回答，若有答不全的，教师(或其他学生)补充．‎ 通过创设情境问题来激发学生学习的兴趣 让学生动手操作，使学生经历知识的发生过程 教师活动内容、方式 学生活动方式 设计意图 ‎3、上节课我们已经学习了：若点P在线段AB的垂直平分线上，那么PA=PB，如果QA=QB，那么点Q在线段AB的垂直平分线上。今天我们又学了若点P在∠‎ 学生思考、猜想、判断 3‎ ‎ ‎ AOB的平分线上，那么点P到OA、OB的距离相等；反过来，你能提出什么猜想吗 部分学生能猜想出来：若点P到OA、OB的距离相等，则点P在∠AOB的平分线上。‎ 让学生完成P24图1-19的相关问题，学生通过作图、测量、观察得到：‎ 到角的两边距离相等的点，在这个角的平分线上。‎ ‎4、上节课我们学习了线段的垂直平分线是到线段两端距离相等的点的集合。那么角平分线就是……？‎ 部分学生会回答出：角平分线是到角两边距离相等的点的集合。‎ 对，既然每一个到角的两边距离相等的点，都在这个角的平分线上，而线是由无数点组成的，所以，我们说：角平分线是到角两边距离相等的点的集合。‎ 完成练习P25、1 ‎ ‎5、例题：任意画∠O，在∠O的两边上分别截取OA、OB，使OA=OB，过点A画OA的垂线，过点B画OB的垂线，设2条垂线相交于点P，点O在∠APB的平分线上吗？为什么？‎ 学生思考，回答，老师用课件给出证明过程：‎ 点O在∠APB的平分线上。‎ 因为OA⊥PA，OB⊥PB，且OA=OB，即点O到∠APB的两边的距离相等，‎ 所以点O在∠APB的平分线上。‎ 理由是：到角的两边距离相等的点在这个角平分线上。‎ 思考：点P也在AOB的平分线上吗?为什么？‎ 完成练习P25、2‎ ‎（三）小结：今天，我们学习了角的轴对称性，角是轴对称图形，对称轴是角平分线所在的直线。角平分线上的点到角的两边距离相等。到角的两边距离相等的点，‎ 引导学生动手实践来验证猜想的结论的正确性。‎ 学生根据课件的演示观察并猜想点O与∠APB的平分线的位置关系；运用合情推理来说明猜想的正确性。‎ 学生板演，共同评议 共同小结 运用类比方法，让学生猜想、判断，意在培养学生独立思考问题、解决问题的能力 这一设计目的在于培养学生良好的思维习惯：设法验证猜想结果。‎ 通过小结，使学生对本课所学内容有一个系统、完整的认识。‎ 教师活动内容、方式 学生活动方式 设计意图 在这个角的平分线上。角平分线是到角两边距离相等的点的集合。‎ 四、补充练习 ‎1. 如图，在△ABC中，∠C = 90°，AD平分∠BAC，且CD = 5，则点D到AB的距离为 . ‎ ‎2. 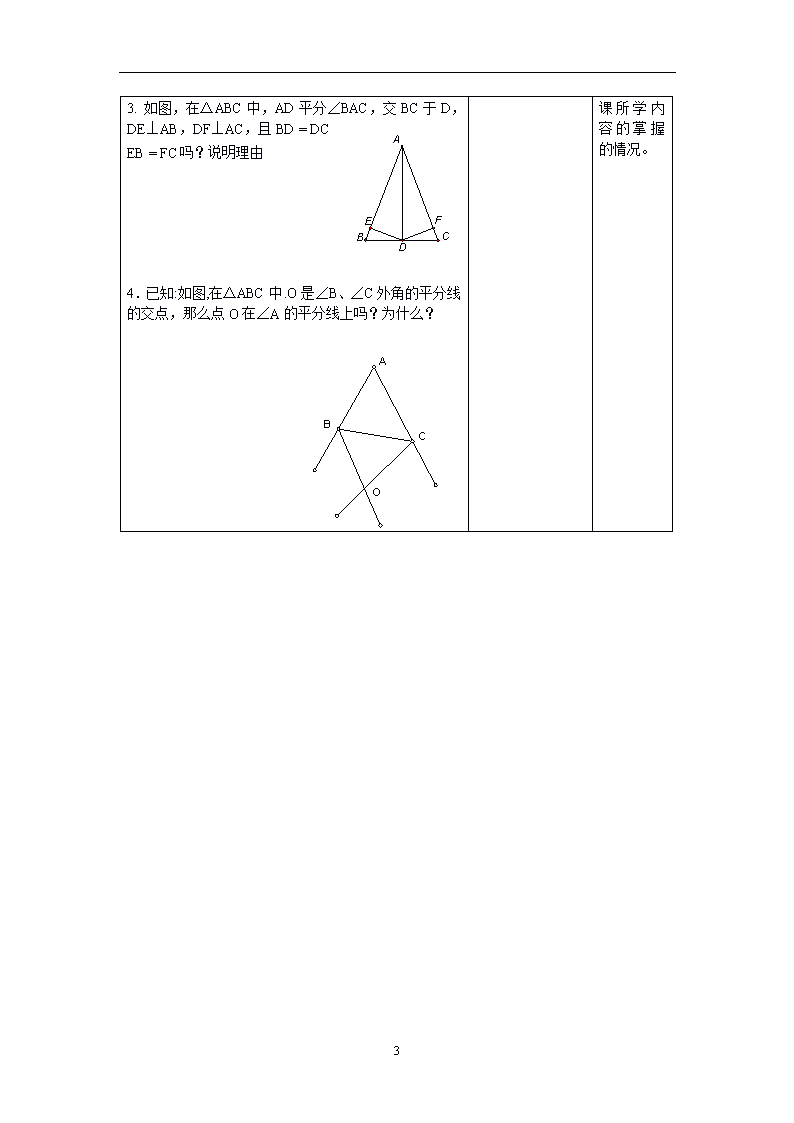在△ABC中，AB=BC，BD平分∠ABC，下列说法不正确的是（）‎ A、BD平分AC B、AD⊥BD ‎ C、AD垂直平分BC， D、BD垂直平分AC 学生练习 3‎ ‎ ‎ ‎3. 如图，在△ABC中，AD平分∠BAC，交BC于D，DE⊥AB，DF⊥AC，且BD = DC EB = FC吗？说明理由 ‎4．已知:如图,在ΔABC中.O是∠B、∠C外角的平分线的交点，那么点O在∠A的平分线上吗？为什么？‎ ‎ ‎ 帮助学生进一步理解巩固本课所学的知识，同时教者也可从学生练习中了解学生对本课所学内容的掌握的情况。‎ ‎　　　　　　　　　‎ 3‎