华师版数学八年级上册课件-第13章-13等腰三角形 20页

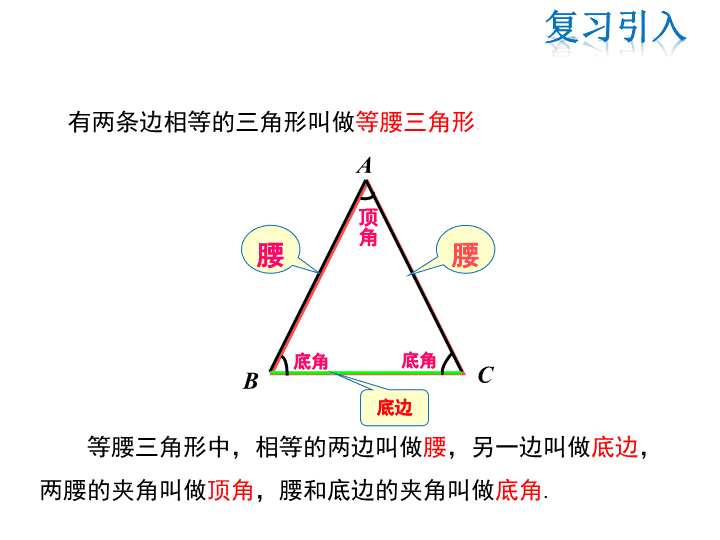
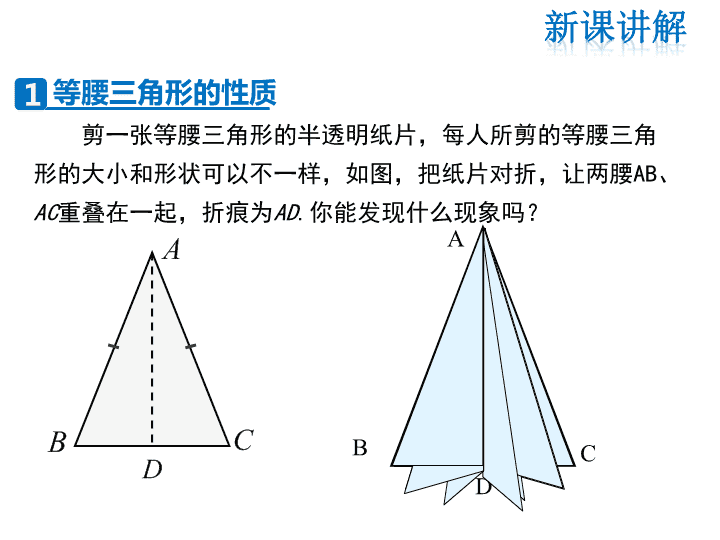
第13章 全等三角形 13.3 等腰三角形 1 等腰三角形的性质 有两条边相等的三角形叫做等腰三角形. 等腰三角形中，相等的两边叫做腰，另一边叫做底边， 两腰的夹角叫做顶角，腰和底边的夹角叫做底角. A CB 腰腰 底边 顶 角 底角底角 剪一张等腰三角形的半透明纸片，每人所剪的等腰三角 形的大小和形状可以不一样，如图，把纸片对折，让两腰AB、 AC重叠在一起，折痕为AD.你能发现什么现象吗？ D A B C A B C D 等腰三角形的性质1 1.等腰三角形是轴对称图形. 我们可以得出结论： A CB D 折痕AD所在直线是等腰三角形的对称轴. 你还有新的发现吗？ ∠B、∠C 是等腰三角形的 .底角 ∠B ＝∠C 所以我们可以描述为:等腰三角形的两个底角相等. 2. 等腰三角形的性质： 等腰三角形的两个底角相等（简写成“等边对等角”）. 【证明】 已知：如图，△ABC 中，AB=AC,求证：∠B=∠C . A B C 分析：由上述操作可以得到启发，即添加等腰三角形的顶角平 分线AD，然后证明△ABD ≌ △ACD. 证明：作顶角∠BAC的平分线AD. 在△ABD与△ACD中， AB＝AC（已知）， ∠1＝∠2（已证）， AD＝AD（公共边）， ∴ △ABD ≌ △ACD（S.A.S.）， ∴ ∠B＝∠C. 从这里你还可以得到什么结论? A B CD ( ( 1 2 【 想一想 刚才的证明除了能得到∠B＝∠C ，你还能发现什么? 重合的线段 重合的角 　 A B D C AB＝AC BD＝CD AD＝AD ∠B ＝ ∠C ∠BAD ＝ ∠CAD ∠ADB ＝∠ADC=90° 【性质】 等腰三角形底边上的高、中线及顶角的平 分线，互相重合（简称“三线合一”）. A B CD ( ( 1 2 【填一填】根据等腰三角形性质完成下列填空. 在△ABC中， AB=AC时， （1）∵AD是底边上的高， ∴∠_____ = ∠_____，____= ____. (2) ∵AD是中线， ∴____⊥____ ，∠_____ =∠_____. (3) ∵AD是角平分线， ∴____ ⊥____ ，_____ =_____. 1 2 2 BD CD AD BC BD 1 BCAD CD 【例1】 已知：在△ABC中 ，AB=AC，∠ B=80 °， 求∠ C和∠ A的大小. A B C ( = 80 ( AB AC C B       已知）, 等边对等角）. =180 ( 180 =180 ( =180 80 80 =20 . A B C A B C                 又 三角形的内角和 等于 ）, 等式的性质） 解： 【例2】 在△ABC中 ，AB=AC，D是BC边上的中点， ∠B=30°.求：（1）∠ ADC的大小；（2）∠1的大小. A D C 1 2 (2)∵∠1 +∠B +∠ADB=180° （三角形内角和等于180°）， ∠B=30° （已知）， ∴∠1=180°-∠B-∠ADB =180°-30°-90°=60°. ∴AD⊥BC(等腰三角形 “三线合一”). ∴∠ADC =∠ADB=90°(垂直的定义). 解：(1) ∵AB = AC，BD=DC（已知）， B 三条边都相等的三角形是等边三角形，它也是轴对称图形， 那么等边三角形的每个角的度数是多少呢？它有几条对称轴？ 等边三角形的性质2 因为等边三角形是特殊的等腰三角形，由等腰三角形等 边对等角的性质得到，∠B＝ ∠ C， 同理可得 ∠A＝∠B, 所以 ∠A＝∠B＝∠C， 又由 ∠A＋∠B＋∠C＝180°， 从而推出 ∠A＝∠B＝∠C＝60°. 也就是说：等边三角形的各个角都相等， 并且每一个角都等于60°. 等边三角形的三条边都相等，三个角 都相等，也称为正三角形. A C B 三条对称轴 A B C D 【例3】 如图，在△ABC中 ，AB=AC，点D在AC上，且 BD=BC=AD，求△ABC各角的度数. （1）找出图中所有相等的角； （2）指出图中有几个等腰三角形？ ∠A=∠ABD, ∠C=∠BDC=∠ABC. △ABC, △ABD, △BCD. A B C D x ⌒ 2x⌒ 2x ⌒ ⌒ 2x （3）观察∠BDC与∠A、∠ABD的关系， ∠ABC、∠C呢？ ∠BDC= ∠A+ ∠ABD=2 ∠A=2 ∠ABD, ∠ABC= ∠BDC=2 ∠A, ∠C= ∠BDC=2 ∠A. （4）设∠A=x,请把△ ABC的内角和用含 x的式子表示出来. ∵ ∠A+ ∠ABC+ ∠ C=180 °， ∴x+2x+2x=180 °. A B C D 解：∵AB=AC，BD=BC=AD， ∴∠ABC=∠C=∠BDC， ∠A=∠ABD. 设∠A=x,则∠BDC= ∠A+ ∠ABD=2x, 从而∠ABC= ∠C= ∠BDC=2x, 于是在△ABC中，有 ∠A+∠ABC+∠C=x+2x+2x=180 ° ， 解得x=36 ° . 在△ABC中，∠A=36°，∠ABC=∠C=72°. x ⌒ 2x ⌒ 2x⌒ ⌒ 2x 1. 如图，在下列等腰三角形中，分别求出它们的底角的度数. A B C 120° A B C 36° ∠B=∠C = 72° ∠B=∠C = 30° 2.(1)等腰三角形一个底角为75°,它的另外两个角为 ； (2)等腰三角形一个角为36°,它的另外两个角为 ____________________； (3)等腰三角形一个角为120°,它的另外两个角为 . 75°, 30° 72°,72°或36°,108° 30°，30° 结论:在等腰三角形中,注意对角的分类讨论. ① 顶角+2×底角=180° ② 顶角=180°－2×底角 ③ 底角=（180°－顶角）÷2 ④0°＜顶角＜180° ⑤0°＜底角＜90° A CB D 3. 如图，是西安半坡博物馆屋顶的截面图，已经知道它的两边 AB和AC是相等的.建筑工人师傅对这个建筑物做出了两个判断: ①工人师傅在测量了∠B为37°以后，并没有测量∠C ，就说 ∠C 的度数也是37°;②工人师傅要加固屋顶，他们通过测量找 到了横梁BC的中点D，然后在AD两点之间钉上一根木桩，他们 认为木桩是垂直横梁的. 请同学们想想,工人师傅的说法对吗？请说明理由. 工人师傅的说法是对的，△ABC是等腰三角形，根 据等腰三角形的性质可以得出这样的结论. A CB D 请同学们想想,工人师傅的说法对吗？请说明理由. 等腰三角 形的性质 等边对等角 等边三角形 注意是指同一个三角形中 注意：顶角的平分线、底边上的 高和中线才有这一性质.而腰上 高、中线和底角的平分线不具有 这一性质 三 线 合 一 有三条对称轴，每个内角等于 60°