2020八年级数学下册 第3章 图形的平移与旋转 第2节《图形的旋转》教案 （新版）北师大版 7页

图形的旋转 教学目标 知识与能力：通过具体事例认识旋转，理解旋转前后两个图形对应点到旋转中心的距离相等，对应点与旋转中心的连线所成的角彼此相等的性质.‎ 过程与方法：经历对生活中与旋转现象有关的图形进行观察、分析、欣赏、以及动手操作、画图等过程，掌握有关画图的操作技能，发展初步的审美能力，增强对图形欣赏的意识.‎ 情感态度价值观：引导学生用数学的眼光看待有关问题，发展学生的数学观，学到活生生的数学.‎ 重点 类比平移与旋转的异同，掌握旋转的定义和基本性质，并利用数学知识解释生活中的旋转现象.‎ 难点 探索旋转的性质，特别是，对应点到旋转中心的距离相等.‎ 教学用具 教学环节 说 明 二次备课 7‎ 新课导入 创设情境，引入新知 演示俄罗斯方块游戏，构成游戏的模块均是由一个小正方形平移变换而来，通过学生玩游戏，发现除了平移运动之外还有旋转运动.引导学生列举出一些具有旋转现象的生活实例，引出课题：“生活中的旋转”。‎ 向学生展示有关的图片：‎ ‎(1)时钟上的秒针在不停的转动；（并介绍顺时针方向和逆时针方向）‎ ‎(2)大风车的转动；‎ ‎(3)飞速转动的电风扇叶片；‎ ‎（4）汽车上的括水器；‎ ‎（5)由平面图形转动而产生的奇妙图案。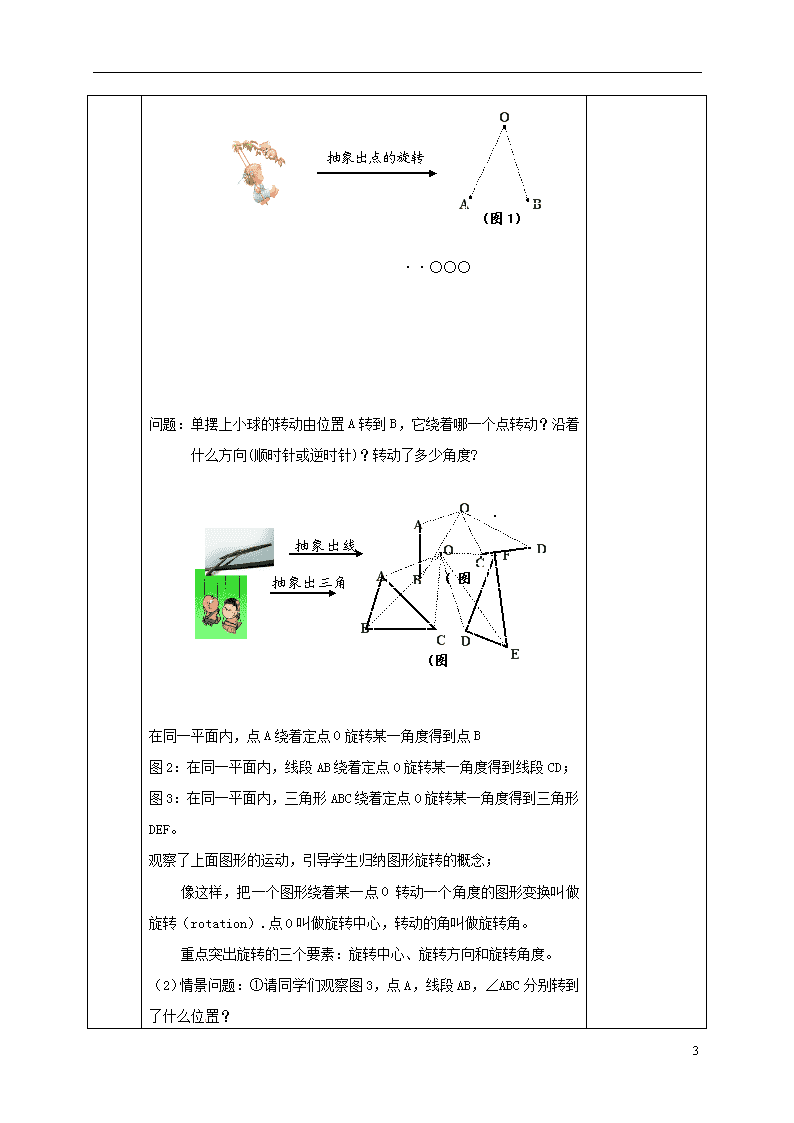‎ ‎ ‎ 课 程 讲 授 ‎　探索新知，形成概念 ‎1.建立旋转的概念 (1) 试一试,请同学们尝试用自己的语言来描述以下旋转.‎ 7‎ 抽象出点的旋转 A B ‎（图1）‎ O ‎ ‎ ‎ ··○○○‎ 抽象出线的旋转 ‎·‎ O A B C D ‎（图2）‎ 问题：单摆上小球的转动由位置A转到B，它绕着哪一个点转动？沿着什么方向(顺时针或逆时针)？转动了多少角度?‎ 抽象出三角形的旋转 ‎·‎ O A B C F D E ‎（图3）‎ ‎ ‎ 在同一平面内，点A绕着定点O旋转某一角度得到点B 图2：在同一平面内，线段AB绕着定点O旋转某一角度得到线段CD；‎ 图3：在同一平面内，三角形ABC绕着定点O旋转某一角度得到三角形DEF。‎ 观察了上面图形的运动，引导学生归纳图形旋转的概念；‎ 像这样，把一个图形绕着某一点O转动一个角度的图形变换叫做旋转（rotation）.点O叫做旋转中心，转动的角叫做旋转角。‎ 重点突出旋转的三个要素：旋转中心、旋转方向和旋转角度。‎ ‎（2）情景问题：①请同学们观察图3，点A，线段AB，∠ABC分别转到了什么位置？‎ 7‎ ‎②请找出图3中其他的对应点、对应线段、对应角，并指出旋转中心和旋转角度。 ‎ 设计意图：点明图形旋转中对应点、对应线段及对应角的概念；让学生及时巩固并理解旋转及其相关概念，并为下面探究旋转的性质作好物质与精神上的准备。‎ ‎2．应用旋转的概念解决问题 ‎ 这一环节让学生进行问题的研究与解答，培养应用数学知识的意识及解决数学问题的能力。‎ （1） 如图，△ABO绕点O旋转得到△CDO，则：‎ 点B的对应点是点_____；‎ C A B O D ‎ 线段OB的对应线段是线段______；‎ 线段AB的对应线段是线段______；‎ ‎∠A的对应角是______；‎ ‎∠B的对应角是______；‎ 旋转中心是点______；‎ 旋转的角是 ______ 。‎ ‎ 设计意图：‎ ① 及时巩固新知，使每个学生都有收获；‎ ‎② 感受成功的喜悦，肯定探索活动的意义。‎ ‎（2） 如图，如果正方形CDEF与正方形ABCD是一边重合的两个正方形，那么正 D C A B E F 方形CDEF能否看成是正方形ABCD旋转得到？如果能，请指出旋转中心、旋转方向、旋转角度及对应点。‎ ‎·‎ ‎·‎ A B O D C ‎（3） 如图，香港特别行政区区旗中央的紫荆花图案由5个相同的花瓣组成,它是由其中的一瓣经过几次旋转得到的?旋转角∠AOB多少度？你知道∠COD等于多少度吗？ ‎ 7‎ ‎ ‎ 实践操作，再探新知 做一做：‎ 如图，在硬纸板上，挖出一个三角形ABC，再挖一个小洞O作为旋转中心，硬纸板下面放一张白纸。先在纸上描出这个挖掉的三角形图案（△ABC），然后围绕旋转中心转动硬纸板，再描出这个挖掉的三角形（△DEF），移开硬‎·‎ O A B C F D E 纸板。‎ 问题：请指出旋转中心和各对应点，哪一个角是旋转角？‎ ‎1．从我们看到的旋转现象以及你所完成的实验中，你认为旋转主要因素是什么？‎ ‎2．在图形的旋转过程中，哪些发生了改变？哪些没有发生改变？‎ 量一量线段OA与线段OD的关系怎样（这里包括数量关系和位置关系），线段OB和OE，OC和OF呢？AB与DE呢？‎ ‎3．你能通过度量角的方法得出旋转角度吗？你准备度量哪个角？‎ 探索得出下列性质：‎ 1． 旋转前后的图形全等；‎ 2． 对应点到旋转中心的距离相等；‎ 3． 对应点与旋转中心连线段的夹角等于旋转角。‎ 第四环节　巩固新知，形成技能 ‎1．如图，如果把钟表的指针看做四边形AOBC，它绕O点旋转得到四边形DOEF.‎ 7‎ 在这个旋转过程中： ‎ ‎（1）旋转中心是什么? ‎ ‎（2）经过旋转，点A，B分别移动到什么位置？‎ O A B D E C F ‎（3）旋转角是什么？‎ ‎（4）AO与DO的长有什么关系？BO与EO呢？‎ ‎（5）∠AOD与∠BOE有什么大小关系？‎ ‎2．如图,正方形ABCD中，E是AD上一点，将△CDE逆时针旋转后得到△CBM.如连接EM,那么△CEM是怎样的三角形?‎ C A B D E M A R P B Q C ‎3．如图：P是等边DABC内的一点，把DABP通过旋转分别得到DBQC和DACR，‎ ‎ （1）指出旋转中心、旋转方向和旋转角度？‎ ‎ （2） DACR是否可以直接通过把DBQC旋转得到？‎ 目的是让学生通过观察图形的特点，发现图形的旋转关系，巩固旋转的性质。‎ （1） 若PA=5，PC=4，PB=3，则△PQC是什么三角形？‎ 小结 引导学生从以下几个方面进行小结：‎ 7‎ ‎⑴这节课你学到了什么?‎ ‎⑵对自己的学习情况进行评价。‎ 作业布置 板书设计 课后反思 7‎