安徽省马鞍山市和县2019-2020学年八年级下学期期末考试数学试题 8页

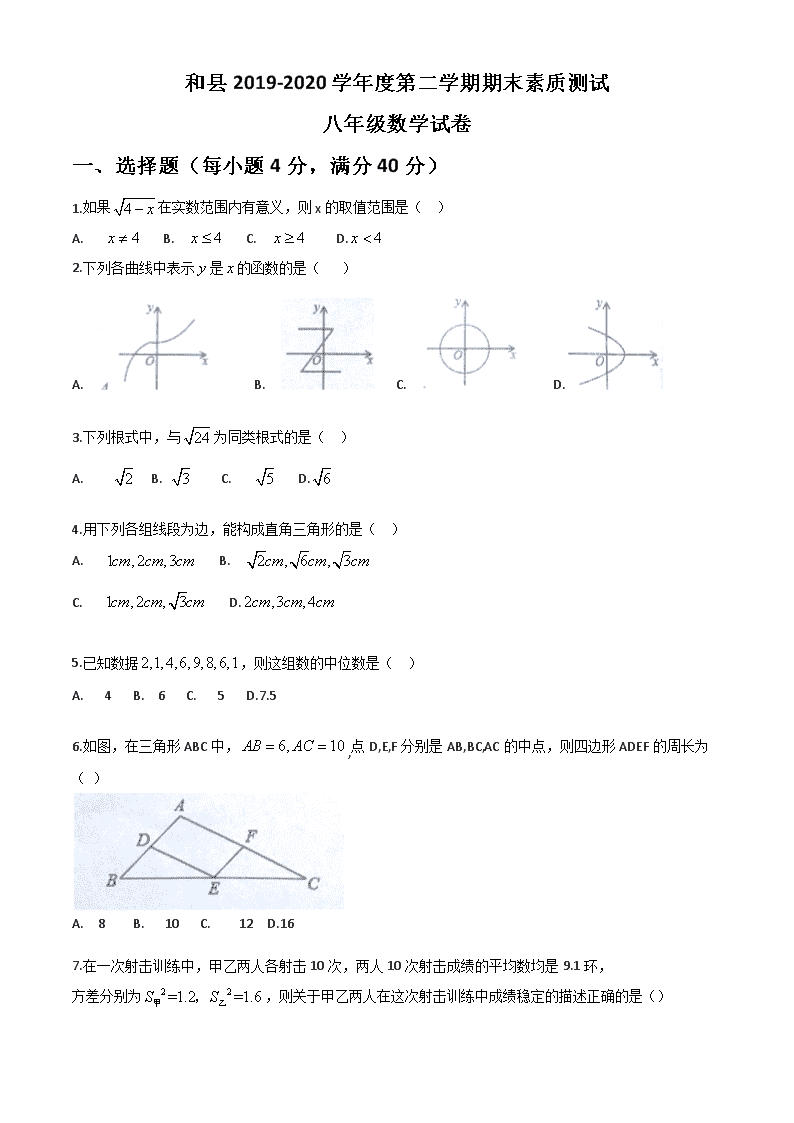
‎ ‎ 和县2019-2020学年度第二学期期末素质测试 八年级数学试卷 一、 选择题（每小题4分，满分40分）‎ ‎1.如果在实数范围内有意义，则x的取值范围是（ ）‎ A. B. C. D.‎ ‎2.下列各曲线中表示是的函数的是（ ）‎ A. B. C. D.‎ ‎3.下列根式中，与为同类根式的是（ ）‎ A. B. C. D.‎ ‎4.用下列各组线段为边，能构成直角三角形的是（ ）‎ A. B. ‎ C. D.‎ ‎5.已知数据，则这组数的中位数是（ ）‎ A. 4 B. 6 C. 5 D.7.5‎ ‎6.如图，在三角形ABC中，,点D,E,F分别是AB,BC,AC的中点，则四边形ADEF的周长为（ ）‎ A. 8 B. 10 C. 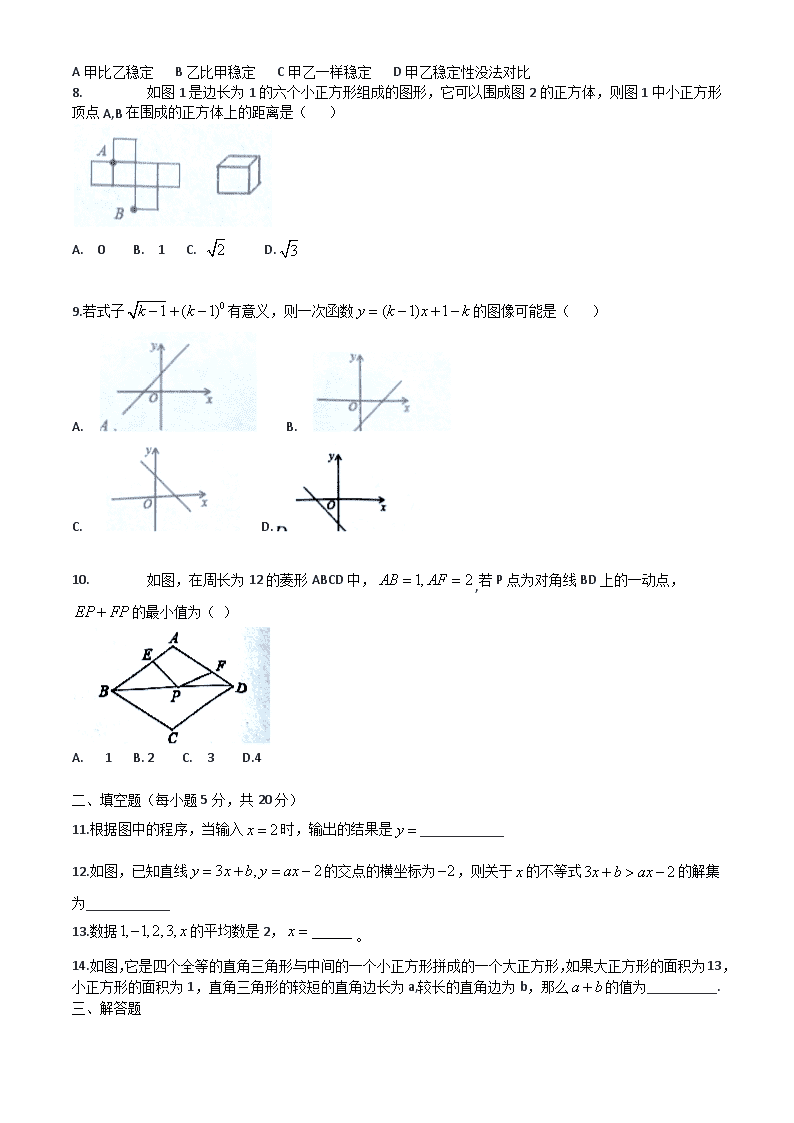12 D.16‎ ‎7.在一次射击训练中，甲乙两人各射击10次，两人10次射击成绩的平均数均是9.1环，‎ 方差分别为，则关于甲乙两人在这次射击训练中成绩稳定的描述正确的是（）‎ ‎ ‎ A甲比乙稳定 B乙比甲稳定 C甲乙一样稳定 D甲乙稳定性没法对比 8. 如图1是边长为1的六个小正方形组成的图形，它可以围成图2的正方体，则图1中小正方形顶点A,B在围成的正方体上的距离是（ ）‎ A. 0 B. 1 C. D.‎ ‎9.若式子有意义，则一次函数的图像可能是（ ）‎ A. B. ‎ C. D.‎ 10. 如图，在周长为12的菱形ABCD中，,若P点为对角线BD上的一动点，的最小值为（ ）‎ A. 1 B. 2 C. 3 D.4‎ 一、 填空题（每小题5分，共20分）‎ ‎11.根据图中的程序，当输入时，输出的结果是____________‎ ‎12.如图，已知直线的交点的横坐标为，则关于的不等式的解集为____________‎ ‎13.数据的平均数是2，。‎ ‎14.如图，它是四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形，如果大正方形的面积为13，小正方形的面积为1，直角三角形的较短的直角边长为a,较长的直角边为b，那么的值为__________.‎ 二、 解答题 ‎ ‎ ‎15.计算：‎ ‎16.已知，求代数式的值 四解答题 ‎17.问题：已知：直线及直线外一点P 求作：直线PQ,使得 下列是小东给出的作法：如图 直线上任取两点A,B作射线AP,‎ 分别以P,B为圆心，长为半径画弧，两弧交于点Q（与P点在直线l的同一侧且不与点A重合）;‎ 作直线PQ，则直线PQ即为所求 根据小东的尺规作图过程，请你：‎ 用直尺和圆规补全图形；‎ 证明：‎ 18. 如图，在四边形ABCD中，E是AD边上的中点，连接BE,并延长BE交CD的延长线于点F，‎ 求证：‎ 一、 ‎（本题共2小题，每小题10分，共20分）‎ ‎19.体育课上，老师为了解女生定点投篮的情况，随机抽取了10名女生进行每人4次定点位置投篮的测试，进球的数统计如图所示 （1） 求女生进球数的平均数、众数 （2） 投球4次，进球3个以上含3个为优秀，全校有女生480人，估计为“优秀”等级的女生约为多少人？‎ ‎ ‎ ‎20.图中的小正方形边长为1，的三个顶点都在小正方形上，求：‎ （1） 三角形ABC的面积；‎ （2） 求三角形ABC边AB上的高CD的长.‎ ‎21.已知是一次函数，且当时，当时 （1） 求这个一次函数的解析式；‎ 求当时，自变量的取值范围.‎ ‎22.某移动通讯公司开设了两种通讯业务：“全球通”使用者先交50元月租费，然后每通话1分钟，再付话费0.4元，“神州行”不缴月租费，每通话1分钟付费0.6元，若一个月内通话x分钟，两种方式的费用分别是元，元。‎ ‎（1）写出与之间的函数关系式；‎ ‎（2）一个月内通话多少分钟，两种移动移动通讯费相同；‎ ‎（3）某人估计一个月内通话300分钟，应选择哪种移动通讯合算些.‎ ‎23.如图，正方形ABCD中，E为BC上一点，过点B作于G，延长BG至点F使.‎ ‎（1）求证：‎ ‎（2）求证：‎ ‎（3）若，求AB的长.‎ ‎ ‎ 试题答案部分 一、 选择题 ‎1-5: BADCC; 6-10: DABBC 二、 填空题 ‎ -1 12. 13. 5 14.5‎ 三、‎ ‎15.解：原式=‎ 16. 解：‎ 四、‎ 17. ‎（1）作图略；‎ （2） 证明：连接BQ，‎ 由作图知 所以四边形ABQP是平行四边形，‎ 所以。‎ 18. 证明：因为四边形ABCD是平行四边形，‎ 所以 所以 因为E是AD的中点，‎ 所以 在三角形ABE和三角形DFE中，‎ ‎ ‎ 所以三角形ABE与三角形DFE全等 所以FD=AB.‎ 16. 解：（1）由条形图得：‎ 女生的平均数是：‎ 因为进球数是3个人数最多，‎ 所以女生进球数的众数为3‎ 答：女生进球数的平均数是2.4，众数是3；‎ ‎（2）样本中优秀率为：‎ 因为全校优秀学生的女生为：‎ 答：全校“优秀”等级的女生人数为240人 ‎20（1）‎ (2) 六 17. 解：（1）设一次函数的解析式为=kx+b,‎ 因为 所以 所以这个一次函数的解析式为：‎ （2） 因为y随着x的增大而减小，‎ 当y=-3时，-3=-x+5,x=8;当y=1时,1=-x+5,x=4‎ 所以当时自变量x的取值范围是：‎ ‎ ‎ 七、‎ 解：（1）‎ ‎（2）‎ 解得 所以通话250分钟两种费用相同。‎ （2） 令x=300,则 所以选择全球通合算 八、‎ 16. ‎（1）证明：因为ABCD是正方形 所以 在三角形BGA中，‎ 因为 过点C作,‎ 因为ABCD是正方形，‎ 所以AB=BC,‎ 由（1）‎ 所以 在三角形CHF中，‎ ‎,‎ 所以.‎ ‎（2）解：在三角形CHF中，‎ ‎ ‎ ‎.‎