九年级数学下册第一章直角三角形的边角关系1从梯子的倾斜程度谈起第1课时习题课件北师大版 41页

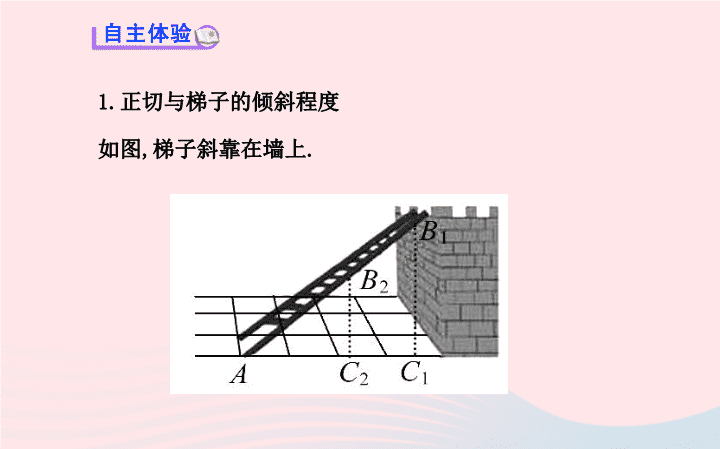
第一章 直角三角形的边角关系 1 从梯子的倾斜程度谈起 第 1 课时 1. 能够用正切表示直角三角形中两边的比，表示生活中物体的倾斜程度、坡度等，能够用正切进行简单计算． ( 重点 ) 2. 理解正切、倾斜程度、坡度的数学意义，密切数学与生活的联系 .( 难点 ) 1. 正切与梯子的倾斜程度 如图 , 梯子斜靠在墙上 . 【 思考 】 (1)△AB 1 C 1 与△ AB 2 C 2 相似吗 ? 为什么 ? 提示 : △AB 1 C 1 与△ AB 2 C 2 相似 .∵∠A=∠A,∠AC 1 B 1 =∠AC 2 B 2 =90°, ∴△AB 1 C 1 ∽△AB 2 C 2 . (2) 如果改变 B 2 在梯子上的位置 , 那么△ AB 1 C 1 与△ AB 2 C 2 _____ ( 填“相似”或“不相似” ). 相似 (3) 根据以上探究可知，无论 B 2 在梯子上的哪个位置，都有 (4) 梯子的倾斜程度与上面的比值有何关系？ 提示： 上面的比值越大，梯子越陡 . 【 总结 】 (1) 正切的定义 : 在 Rt△ABC 中 , 如果锐角 A 确定 , 那么∠ A 的 _____ 与 _____ 的比便 随之确定 , 这个比叫做∠ A 的正切 , 记作 _____ . (2) 梯子的倾斜程度与正切的关系 : 如果梯子与地面的夹角为∠ A, 那么 tanA 的值 _____ , 梯子越陡 . 对边 邻边 tanA 越大 2. 坡度 坡面的 _________ 与 _________ 的比称为坡度 ( 或 _____), 山坡 的坡度常用 _____ 描述 . 铅直高度 水平宽度 坡比 正切 ( 打“√”或“ ×”) (1) 一个角所在的直角三角形越大，这个角的正切值也越 大 .( ) (2) 一个角的正切值只与这个角的大小有关 .( ) (3) 只有直角三角形中的角才有正切值 .( ) (4) 一个斜坡的坡角越大，坡度也越大 .( ) (5) 在△ ABC 中， ( ) × √ × √ × 知识点 1 求锐角的正切值 【 例 1】 已知△ ABC 中， AB=AC ， BD 是 AC 边上的中线， AB=13 ， BC=10. 求 tan ∠DBC 的值． 【 思路点拨 】 作高 AH ， DF⊥BC→ 求出 AH 的长→求出 DF 的长→ 在 Rt△DBF 中求出 tan ∠DBC 的值 . 【 自主解答 】 过点 A,D 分别作 AH⊥BC,DF⊥BC ，垂足分别为 点 H,F. ∵AB=AC ， AH⊥BC ， 在 Rt△ABH 中， ∵ AH∥DF ，且 BD 是 AC 边上的中线， ∴在 Rt△DBF 中， 【 总结提升 】 利用定义求锐角的正切值的 “ 三步法 ” 1. 观察：观察所给的锐角是否在直角三角形中 . 2. 转化：如果所给的锐角不在直角三角形中，可通过作辅助线构造直角三角形或利用等量关系代换将锐角 “ 转移 ” 到直角三角形中 . 3. 求解：在直角三角形中求出这个角的对边与邻边的比值，就是这个角的正切值 . 知识点 2 正切的应用 【 例 2】 如图，一段河坝的横断面为梯形 ABCD ，试根据图中的数据，求出坝底宽 AD ． (i=CE∶ED ，单位： m) 【 解题探究 】 1.ED 与 CE 有什么关系 ?ED 的长是多少 ? 提示 : ∵i=CE∶ED=1∶2, ∴ED=2CE=2×4=8(m). 2. 如图 , 过点 B 作 BF⊥AD 于 F, 则四边形 BFEC 是什么形状的特殊 四边形 ?EF,BF 的长是多少 ? 提示 : 四边形 BFEC 是正方形 , 则 EF=BF=BC=4 m. 3. 可求出 AF 的长是多少？那么即可求出坝底宽 AD. 提示： 在 Rt△ABF 中，由勾股定理可得： 根据以上探究，可得坝底 AD ＝ AF+FE+ED ＝ 3+4+8 ＝ 15(m) ． 【 互动探究 】 在上题中，斜坡 AB 的坡度是多少？ 提示： 在 Rt△AFB 中，因 BF=4 ， AF=3 ，所以斜坡 AB 的坡度 为 【 总结提升 】 坡度的常见用法和两点注意 坡度的常见用法： (1) 坡度常和实际生活中的问题相结合，如拦水坝、开渠、修路等 . (2) 坡度常和梯形的知识相结合，解题时常把梯形转化为三角形和矩形求解 . 两点注意： (1) 坡度是两条线段的比值，不是度数 . (2) 坡度是铅直高度与水平宽度的比，而不是斜面距离与水平宽度 ( 或铅直高度 ) 的比 . 题组一：求锐角的正切值 1. 如图，在 8×4 的矩形网格中，每个小正方形的边长都是 1 ， 若△ ABC 的三个顶点在图中相应的格点上，则 tan ∠ACB 的值 为 ( ) 【 解析 】 选 A ．如图，在网格中构造含有∠ ACB 的 Rt△ACD ， 在该三角形中 2. 某时刻海上点 P 处有一客轮，测得灯塔 A 位于客轮 P 的北偏东 30° 方向，且相距 20 海里．客轮以 60 海里 / 小时的速度沿北偏 西 60° 方向航行 小时到达 B 处，那么 tan ∠ABP ＝ ( ) 【 解析 】 选 A ．如图，在△ PAB 中，∠ APB ＝ 60° ＋ 30° ＝ 90° ， PA ＝ 20 海里， ( 海里 ) ， 故 3.(2013· 济南中考 ) 已知直线 l 1 ∥ l 2 ∥ l 3 ∥ l 4 ，相邻的两条 平行直线间的距离均为 h ，矩形 ABCD 的四个顶点分别在这四 条直线上，放置方式如图所示， AB=4 ， BC=6 ，则 tan α 的值 等于 ( ) 【 解析 】 选 C. 如图，作 AM⊥ l 4 于点 M ，作 CN⊥ l 4 于点 N ， 则 AM=h ， CN=2h ，∠ ABM+∠BAM=90° ， ∵四边形 ABCD 是矩形，∴∠ ABC=90° ， ∴∠ ABM+∠α=90° ，∴∠ BAM=∠α ， ∴△ ABM∽△BCN ， ∴ BM=AM · tan α=htan α ， ∴ 4. 在△ ABC 中，∠ C=90° ， AB=5 ， BC=4 ，则 tan A=______. 【 解析 】 由勾股定理，得 答案： 5. 如图，在△ ABC 中， AC ＝ 4 ， BC ＝ 3 ， CD⊥AB 于点 D ， BD ＝ 2, 求 tan A ， tan B 的值 . 【 解析 】 在 Rt△BDC 中， BC ＝ 3 ， BD ＝ 2 ， 在 Rt△ADC 中 , 题组二： 正切的应用 1. 如图，在平地上种植树木时， 要求株距 ( 相邻两树间的水平距 离 ) 为 4 m. 如果在坡度为 0.75 的 山坡上种树，也要求株距为 4 m, 那么相邻两树间的坡面距离为 ( ) A.5 m B.6 m C.7 m D.8 m 【 解析 】 选 A. 由题意可得 , 如图， AC=4 m ， tan A=0.75, 则 故 BC=3 m ， 则 2.(2013· 聊城中考 ) 河堤横断面如图所示，堤高 BC=6 m ，迎水 坡 AB 的坡比为 则 AB 的长为 ( ) 【 解析 】 选 A. 在 Rt△ABC 中， 【 变式备选 】 河堤横断面如图所示，迎水坡 AB 的坡比为 AB 的长是 10 m ，则堤高 BC=______ m ． 【 解析 】 在 Rt△ABC 中， 答案： 5 3.(2013· 安顺中考 ) 在 Rt△ABC 中， 则△ ABC 的面积为 ______. 【 解析 】 ∵Rt△ABC 中， 解得 CA=6 ， 答案： 24 4. 某人沿着有一定坡度的坡面前进了 10 m ，此时他与水平地面 的垂直距离为 则这个坡面的坡度为 ______ ． 【 解析 】 如图， 由勾股定理，得 ∴斜坡 AB 的坡度 答案： 1∶2 5. 如图 , 拦水坝的横断面为梯形 ABCD, 坝顶宽 AD=5m, 斜坡 AB 的坡度 i =1∶3( 指坡面的铅直高度 AE 与水平宽度 BE 的比 ), 斜坡 DC 的坡度 i=1∶1.5, 已知该拦水坝的高为 6m. (1) 求斜坡 AB 的长 . (2) 求拦水坝的横断面梯形 ABCD 的周长 . ( 注意：本题中的计算过程和结果均保留根号 ) 【 解析 】 (1) 在 Rt△ABE 中，根据勾股定理得， 答：斜坡 AB 的长为 (2) 过点 D 作 DF⊥BC 于点 F ， ∴四边形 AEFD 是矩形 . ∴EF=AD=5 m. 又 ∴BC=BE ＋ EF ＋ FC=18 ＋ 5 ＋ 9=32(m). 在 Rt△DCF 中，根据勾股定理得， ∴梯形 ABCD 的周长为 AB ＋ BC ＋ CD ＋ DA 答：梯形 ABCD 的周长为 【 想一想错在哪？ 】 如图，△ ABC 中，∠ C=90° ， BC=6 cm ， △ ABC 的面积是多少？ 提示： 对正切的定义理解不透彻，搞错了边之间的比 .