2015年辽宁锦州中考真题数学试卷（详解 16页

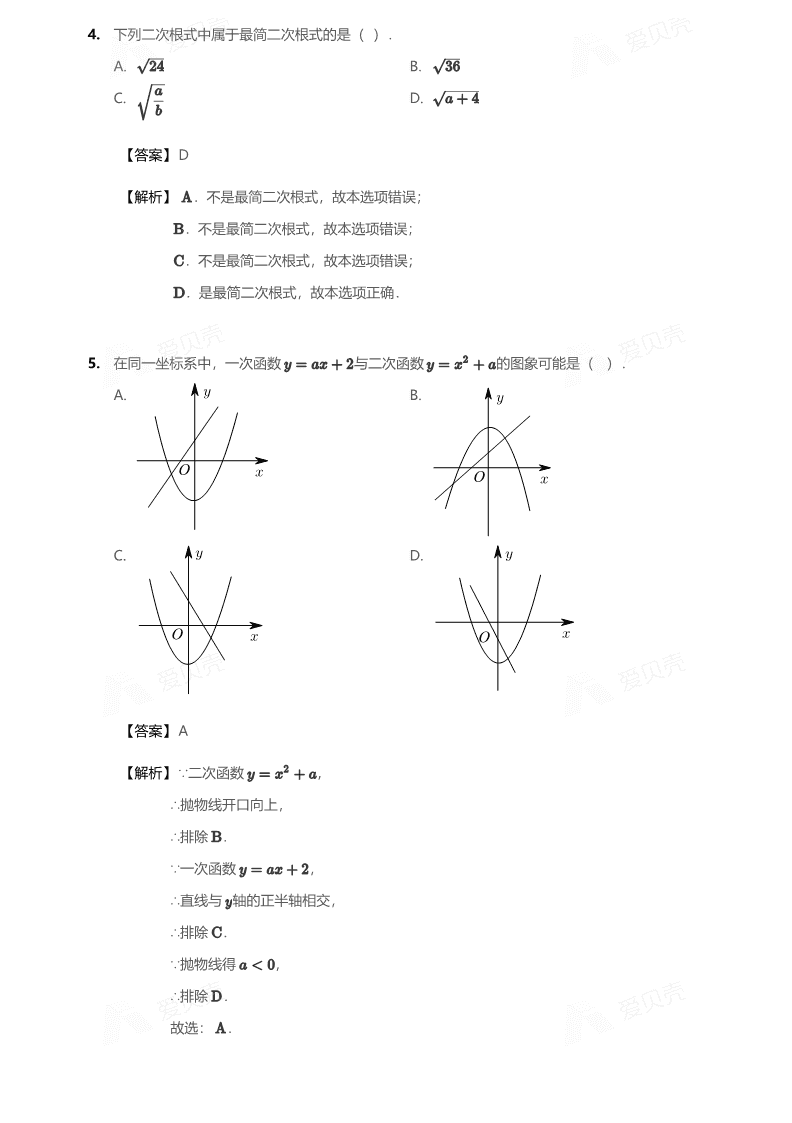
/ 2015年辽宁锦州中考真题数学试卷(详解) 一、选择题（每小题3分，共24分） 1. A. B. C. D. 【答案】 【解析】 的相反数是（ ）． B 根据相反数的定义即可得， 的相反数是 ． 2. A. 明天我市下雨 B. 抛一枚硬币，正面朝下 C. 购买一张福利彩票中奖了 D. 掷一枚骰子，向上一面的数字一定大于零 【答案】 【解析】 下列事件中，属于必然事件的是（ ）． D ∵ 、 、 选项为不确定事件，即随机事件，故不符合题意． ∴一定发生的事件只有 ，掷一枚骰子，向上一面的数字一定大于零，是必然事件， 符合题意． 3. A. B. C. D. 【答案】 【解析】 如图是由四个相同的小正方体组成的立体图形，它的左视图为（ ）． A 从左面看，这个立体图形有两层，且底层有两个小正方形，第二层的左边有一个小 正方形． / 4. A. B. C. D. 【答案】 【解析】 下列二次根式中属于最简二次根式的是（ ）． D ．不是最简二次根式，故本选项错误； ．不是最简二次根式，故本选项错误； ．不是最简二次根式，故本选项错误； ．是最简二次根式，故本选项正确． 5. A. O B. O C. O D. O 【答案】 【解析】 在同一坐标系中，一次函数 与二次函数 的图象可能是（ ）． A ∵二次函数 ， ∴抛物线开口向上， ∴排除 ． ∵一次函数 ， ∴直线与 轴的正半轴相交， ∴排除 ． ∵抛物线得 ， ∴排除 ． 故选： ． / 6. A. B. C. D. 【答案】 【解析】 不等式组 的解集在数轴上表示正确的是（ ）． B 由 得： ， 由 得： ， ∴不等式组的解集为 ． ∴不等式组 的解集在数轴上表示正确的是 选项． 7. A. 有两个相等的实数根 B. 有两个不相等的实数根 C. 只有一个实数根 D. 没有实数根 【答案】 【解析】 一元二次方程 的根的情况为（ ）． A ∵ ， ， ， ∴ ， ∴方程有两个相等的实数根． 8. A. ， B. ， C. ， D. ， 【答案】 【解析】 如图，线段 两个端点的坐标分别为 ， ，以原点 为位似中心，在第一象限内 将线段 缩小为原来的 后得到线段 ，则端点 和 的坐标分别为（ ）． C ∵线段 两个端点的坐标分别为 ， ，以原点 为位拟中心，在第一 象限内将线段 缩小为原来的 后得到线段 ， ∴端点的坐标为： ， ． / 二、填空题（每小题3分，共24分） 9. 【答案】 【解析】 已知地球上海洋面积约为 ， 这个数用科学记数法可表示 为 ． 用科学记数法表示较大的数的形式为 ，其中 ， 为整数且 的 值为这个数的整数位数减 ，这里 ，所以 .， 10. 【答案】 【解析】 数据 ， ， ， ， 的众数是 ． 一组数据中出现次数最多的数据叫做众数，根据众数的定义可得数据 ， ， ， ， 中 出现的次数最多，所以这一组数据的众数是 ． 11. 【答案】 【解析】 如图，已知 ， ， ， ． ∵ ， ∴ ， ∵ 为 的一个外角， ∴ ． 12. 【答案】 【解析】 分解因式： ． 分解因式： ． 13. / 【答案】 【解析】 如表记录了一名球员在罚球线上投篮的结果．那么，这名球员投篮一次，投中的概率约 为 （精确到 ）． 投篮次数（ ） 投中次数（ ） 投中频率（ ） 由题意得，这名球员投篮的次数为 次，投中的次数为 ， 故这名球员投篮一次，投中的概率约为： ． 14. 【答案】 【解析】 如图，点 在双曲线 上， 轴于点 ，且 的面积是 ，则 的值是 ． ∵ 的面积是 ， ∴ ， ∴ ，解得 ， 又∵双曲线 的图象经过第二、四象限， ∴ ，即 的值是 ． 15. 【答案】 【解析】 制作某种机器零件，小明做 个零件与小芳做 个零件所用的时间相同，已知小明每小时比 小芳多做 个零件．设小芳每小时做 个零件，则可列方程为 ． 设小芳每小时做 个零件，则小明每小时做 个零件，由题意得， ． / 16. 【答案】 【解析】 如图，在平面直角坐标系中，边长不等的正方形依次排列，每个正方形都有一个顶点落在函数 的图象上，从左向右第 个正方形中的一个顶点 的坐标为 ，阴影三角形部分的 面积从左向右依次记为 、 、 、 、 ，则第 个正方形的边长是 ， 的值 为 ． ; 直线 与正方形的边围成的三角形直角边底是高的 倍， ∵ ， ∴第一个正方形的边长为 ，第二个正方形的边长为 ，第三个正方形的边长为 ， 第四个正方形的边长为 ，第五个正方形的边长为 ， ，由图可知， ， ， ， ∴ ． 三、解答题（每小题8分，共16分） 17. 【答案】 【解析】 先化简，再求值： ，其中 ． ． 原式 ， 当 时，原式 ． 18. 如图，在平面直角坐标系中，线段 的两个端点是 ， ，线段 的两个端点 是 ， ． / （ 1 ） （ 2 ） （ 1 ） （ 2 ） 【答案】 （ 1 ） （ 2 ） 【解析】 线段 与线段 关于直线对称，则对称轴是 ． 平移线段 得到线段 ，若点 的对应点 的坐标为 ，画出平移后的线段 ，并写出点 的坐标为 ． 轴 ∵ ， ， ∴ 轴，且到 轴的距离相等，同理 轴，且到 轴的距离相等， ∴线段 和线段 关于 轴对称． ∵ ， ， ∴相当于把 点先向右平移 个单位，再向上平移一个单位， ∵ ， ∴平移后得到 的坐标为 ，线段 如图所示， 四、解答题（每小题10分，共20分） 19. 年 月，某校组织了以“德润书香”为主题的电子小报制作比赛，评分结果只有 ， ， ， ， 五种，现从中随机抽取部分作品，对其份数和成绩进行整理，制成如下两幅不完 整的统计图： / （ 1 ） （ 2 ） （ 1 ） （ 2 ） 【答案】 （ 1 ） （ 2 ） 【解析】 根据以上信息，解答下列问题： 求本次抽取了多少份作品，并补全两幅统计图． 已知该校收到参赛作品共 份，比赛成绩达到 分以上（含 分）的为优秀作品，据 此估计该校参赛作品中，优秀作品有多少份？ （份），统计图见解析． 估计该校参赛作品中，优秀作品有 份． 根据题意得： （份），得 分的作品数为 （份）， 补全统计图，如图所示: 根据题意得： （份），则据此估计该校参赛作品中，优 秀作品有 份． 20. （ 1 ） （ 2 ） （ 1 ） （ 2 ） 【答案】 （ 1 ）【解析】 育才中学计划召开“诚信在我心中”主题教育活动，需要选拔活动主持人，经过全校学生投票推 荐，有 名男生和 名女生被推荐为候选主持人． 小明认为，如果从 名候选主持人中随机选拔 名主持人，不是男生就是女生，因此选出 的主持人是男生和女生的可能性相同，你同意他的说法吗？为什么？ 如果从 名候选主持人中随机选拔 名主持人，请通过列表或树状图求选拔出的 名主持人 恰好是 名男生和 名女生的概率． 不同意． （恰好是 名男生和 名女生） ． 不同意．理由如下： ∵有 名男生和 名女生， / （ 2 ） ∴主持人是男生的概率 ，主持人是女生的概率 ． 画出树状图如下： 一共有 种情况，恰好是 名男生和 名女生的有 种情况， 所以， （恰好是 名男生和 名女生） ． 五、解答题（每小题10分，共20分） 21. 【答案】 【解析】 如图， 中，点 ， 分别是边 ， 的中点，连接 ， ，点 在 的延长线 上，且 ，连接 ，判断四边形 的形状，并加以证明． 四边形 是平行四边形． 四边形 是平行四边形，证明如下： ∵点 、 分别是边 、 的中点， ∴ ， ， ∵ ， ∴ ， ∴四边形 是平行四边形． 22. 如图，三沙市一艘海监船某天在黄岩岛 附近海域由南向北巡航，某一时刻航行到 处，测得该 岛在北偏东 方向，海监船以 海里/时的速度继续航行， 小时后到达 处，测得该岛在北偏 东 方向，求此时海监船与黄岩岛 的距离 的长．（参考数据： ，结果精确到 ） / 【答案】 【解析】 （黄岩岛） 北 东 海里． 过 作 于 ， （黄岩岛） 北 东 由已知条件得： ， ， 在 中， ∵ ， ， ∴ ， 在 中， ∵ ， ∴ 海里． 六、解答题（每小题10分，共20分） 23. 如图， 中，以 为直径的⊙ 与边 交于点 ，点 为⊙ 上一点，连接 并延长 交 于点 ，连接 ． / （ 1 ） （ 2 ） （ 1 ） （ 2 ） 【答案】 （ 1 ） （ 2 ） 【解析】 若 ，求证： 是⊙ 的切线． 若 ， ， ，求⊙ 的直径． 证明见解析． ⊙ 的直径为 ． ∵ ， ， ∴ ， ∵ ， ∴ ， ∴ ， ∴ 是⊙ 的切线． ∵ ， ， ∴ ， ∴ ， ∴ ， 解得： ， 即⊙ 的直径为 ． 24. （ 1 ） （ 2 ） （ 3 ） （ 1 ） （ 2 ） 【答案】 开学初，小明到文具批发部一次性购买某种笔记本，该文具批发部规定：这种笔记本售价 （元/ 本）与购买数量 （本）之间的函数关系如图所示． 图中线段 所表示的实际意义是 ． 请直接写出 与 之间的函数关系式． 已知该文具批发部这种笔记本的进价是 元/本，若小明购买此种笔记本超过 本但不超 过 本，那么小明购买多少本时，该文具批发部在这次买卖中所获的利润 （元）最 大？最大利润是多少？ 购买不超过 本此种笔记本时售价为 元/本． ． / （ 3 ） （ 1 ） （ 2 ） （ 3 ） 【解析】 当小明购买 本时，该文具批发部在这次买卖中获得的利润最大，最大利润 是 元． 图中线段 所表示的实际意义是：购买不超过 本此种笔记本时售价为 元/本． ①当 时， 与 之间的函数关系式 ． ②当 时，设 把 ， 代入得： ， 解得： ， ∴ 与 之间的函数关系式 ． ③当 时， 与 之间的函数关系式 ， ∴ ． ， ∴当小明购买 本时，该文具批发部在这次买卖中获得的利润最大，最大利润 是 元． 七、解答题（本题12分） 25. （ 1 ） （ 2 ） 如图①， 的顶点 在正方形 两条对角线的交点处， ，将 绕 点 旋转，旋转过程中 的两边分别与正方形 的边 和 交于点 和点 （点 与点 ， 不重合）． 图 如图①，当 时， ， ， 之间满足的数量关系是 ． 如图②，将图①中的正方形 改为 的菱形，其他条件不变，当 时，（ ）中的结论变为 ，请给出证明． / （ 3 ） （ 1 ） （ 2 ） （ 3 ） 【答案】 （ 1 ） （ 2 ） 【解析】 图 在（ ）的条件下，若旋转过程中 的边 与射线 交于点 ，其他条件不变， 探究在整个运动变化过程中， ， ， 之间满足的数量关系，直接写出结论，不 用加以证明． 图 ． 证明见解析． ①当点 落在 上时， ， ②当点 落在 的延长线上时， ． 正方形 的对角线 、 交于点 ， ∴ ， ， ∵ ， ∴ ， 在 和 中， ∵ ， ， ， ∴ ≌ （ ）， ∴ ， ∴ ． 如图，取 的中点 ，连接 ， / （ 3 ） 图 ∵四边形 为 的菱形， ∴ ， ， ， ∴ 是等边三角形， ∴ ， ， ∵ ， ∴ ， ∵ ， ∴ ， 在 和 中， ∵ ， ， ， ∴ ≌ （ ）， ∴ ， ∴ ． 如图，在整个运动变化过程中， ①当点 落在 上时， ， ②当点 落在 的延长线上时， ． （如图 ，取 中点 ，连接 ，证明 ≌ ） 图 八、解答题（本题14分） 26. / （ 1 ） （ 2 ） （ 3 ） （ 1 ） （ 2 ） （ 3 ） 【答案】 （ 1 ） （ 2 ） 【解析】 如图，在平面直角坐标系中，抛物线 经过点 和点 ，且与 轴 交于点 ，点 的坐标为 ，点 是该抛物线上的一个动点，连接 ， ， ， ． 备用图 求该抛物线的解析式． 当 的面积等于 的面积时，求点 的坐标． 当 ， 时，过点 作直线 轴于点 交直线 于点 ，过点 作 轴于点 ，连接 ，请直接写出随着点 的运动，线段 的最小值． ． 点 的坐标是 或 或 或 ． 线段 的最小值是 ． 把 ， 两点的坐标代入 ， 可得： ， 解得： ， ∴抛物线的解析式为： ． ∵抛物线的解析式为： ， ∴点 的坐标是 ， ∵点 ，点 ， ∴ ， ∴ 的面积 ， ∴ 的面积 ， ∵点 ，点 ， ∴ ， ∴ ， ∴ 或 ， ①当 时， ，即： ， 解得 或 ， ∴点 的坐标是 或 ； / （ 3 ） ②当 时， ，整理得： ， 解得 或 ， ∴点 的坐标是 或 ； 综上，可得点 的坐标是 或 或 或 ． 如图，设 所在的直线的解析式是： ， ∵点 的坐标是 ，点 的坐标是 ， ∴ ，解得： ， ∴ 所在的直线的解析式是： ， ∵点 的坐标是 ， ∴点 的坐标是 ， ∴ ， ∵ ， ∴ 时，线段 的最小值是： ， 即线段 的最小值是 ．