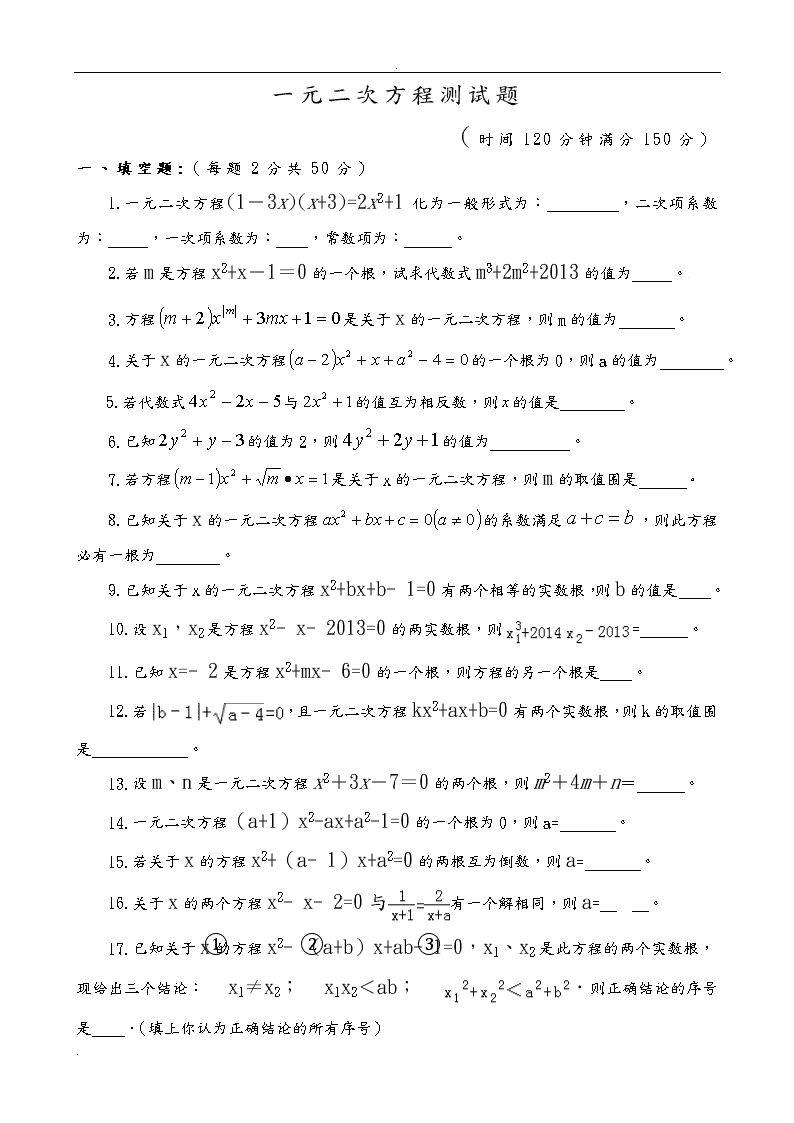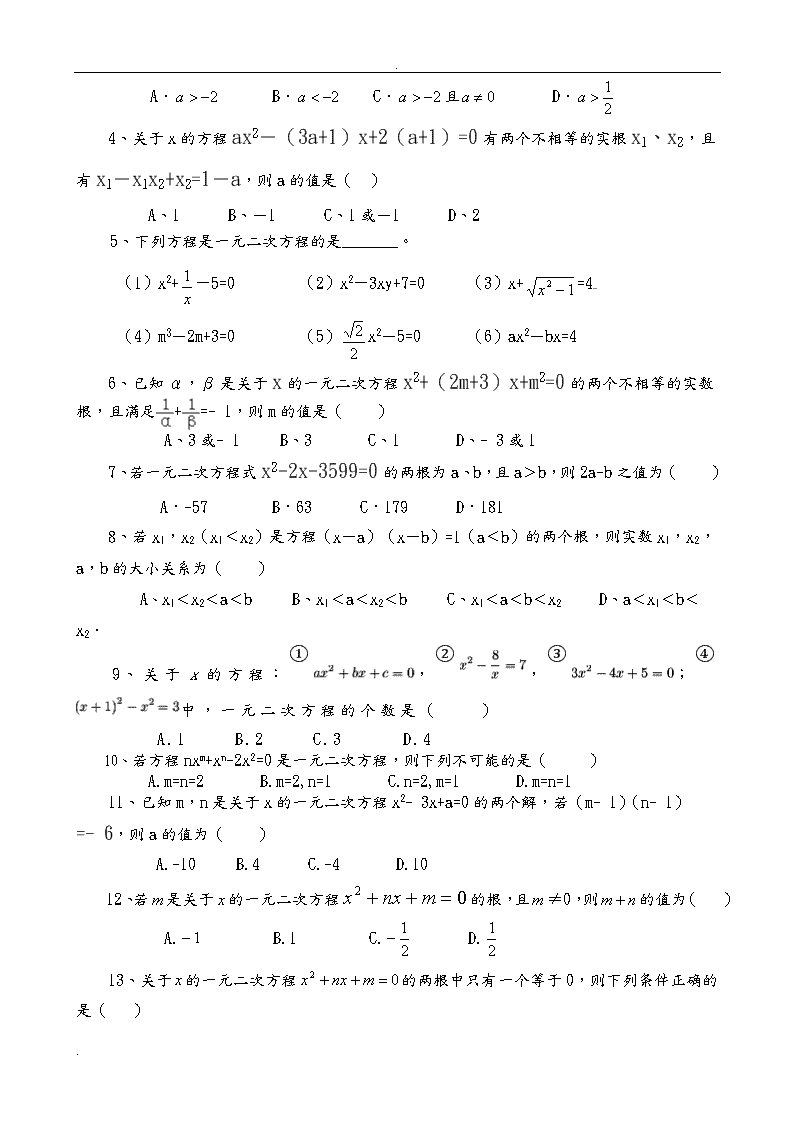- 360.50 KB
- 2021-11-06 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
.
一元二次方程测试题
(时间120分钟满分150分)
一、填空题:(每题2分共50分)
1.一元二次方程(1-3x)(x+3)=2x2+1 化为一般形式为: ,二次项系数为: ,一次项系数为: ,常数项为: 。
2.若m是方程x2+x-1=0的一个根,试求代数式m3+2m2+2013的值为 。
3.方程是关于x的一元二次方程,则m的值为 。
4.关于x的一元二次方程的一个根为0,则a的值为 。
5.若代数式与的值互为相反数,则的值是 。
6.已知的值为2,则的值为 。
7.若方程是关于x的一元二次方程,则m的取值围是 。
8.已知关于x的一元二次方程的系数满足,则此方程必有一根为 。
9.已知关于x的一元二次方程x2+bx+b﹣1=0有两个相等的实数根,则b的值是 。
10.设x1,x2是方程x2﹣x﹣2013=0的两实数根,则= 。
11.已知x=﹣2是方程x2+mx﹣6=0的一个根,则方程的另一个根是 。
12.若,且一元二次方程kx2+ax+b=0有两个实数根,则k的取值围是 。
13.设m、n是一元二次方程x2+3x-7=0的两个根,则m2+4m+n= 。
14.一元二次方程(a+1)x2-ax+a2-1=0的一个根为0,则a= 。
15.若关于x的方程x2+(a﹣1)x+a2=0的两根互为倒数,则a= 。
16.关于x的两个方程x2﹣x﹣2=0与有一个解相同,则a= 。
17.已知关于x的方程x2﹣(a+b)x+ab﹣1=0,x1、x2是此方程的两个实数根,现给出三个结论:①x1≠x2;②x1x2<ab;③.则正确结论的序号是 .(填上你认为正确结论的所有序号)
.
.
18.a是二次项系数,b是一次项系数,c是常数项,且满足+(b-2)2+|a+b+c|=0,满足条件的一元二次方程是 。
19.巳知a、b是一元二次方程x2-2x-1=0的两个实数根,则代数式(a-b)(a+b-2)+ab的值等于____.
20.已知关于x的方程x2+(2k+1)x+k2-2=0的两实根的平方和等于11,则k的值为 .
21.已知分式,当x=2时,分式无意义,则a= ;当a<6时,使分式无意义的x的值共有 个.
22.设x1、x2是一元二次方程x2+5x﹣3=0的两个实根,且,则a= 。
23. 方程的较大根为r,方程的较小根为s,则s-r的值为 。
24. 若 。
25. 已知是方程的两个根,是方程的两个根,则m的值为 。
二、选择题:(每题3分共42分)
1、关于的一元二次方程的一个根是,则的值为( )
A. B. C.或 D.
2、关于x2=-2的说法,正确的是 ( )
A.由于x2≥0,故x2不可能等于-2,因此这不是一个方程
B.x2=-2是一个方程,但它没有一次项,因此不是一元二次方程
C.x2=-2是一个一元二次方程
D.x2=-2是一个一元二次方程,但不能解
3、若是关于的一元二次方程,则不等式的解集是( )
.
.
A. B. C.且 D.
4、关于x的方程ax2-(3a+1)x+2(a+1)=0有两个不相等的实根x1、x2,且有x1-x1x2+x2=1-a,则a的值是( )
A、1 B、-1 C、1或-1 D、2
5、下列方程是一元二次方程的是_______。
(1)x2+-5=0 (2)x2-3xy+7=0 (3)x+=4
(4)m3-2m+3=0 (5)x2-5=0 (6)ax2-bx=4
6、已知α,β是关于x的一元二次方程x2+(2m+3)x+m2=0的两个不相等的实数根,且满足+=﹣1,则m的值是( )
A、3或﹣1 B、3 C、1 D、﹣3或1
7、若一元二次方程式x2-2x-3599=0的两根为a、b,且a>b,则2a-b之值为( )
A.-57 B.63 C.179 D.181
8、若x1,x2(x1<x2)是方程(x-a)(x-b)=1(a<b)的两个根,则实数x1,x2,a,b的大小关系为( )
A、x1<x2<a<b B、x1<a<x2<b C、x1<a<b<x2 D、a<x1<b<x2.
9、关于x的方程:①,②,③;④中,一元二次方程的个数是( )
A.1 B.2 C.3 D.4
10、若方程nxm+xn-2x2=0是一元二次方程,则下列不可能的是( )
A.m=n=2 B.m=2,n=1 C.n=2,m=1 D.m=n=1
11、已知m,n是关于x的一元二次方程x2﹣3x+a=0的两个解,若(m﹣1)(n﹣1)=﹣6,则a的值为( )
A.-10 B.4 C.-4 D.10
12、若是关于的一元二次方程的根,且≠0,则的值为( )
A. B.1 C. D.
13、关于的一元二次方程的两根中只有一个等于0,则下列条件正确的是( )
.
.
A. B. C. D.
14、若方程中,满足和,则方程的根是( )
A.1,0 B.-1,0 C.1,-1 D.无法确定
三、计算题:(1.2.3.4.5.6每题5分,.7.8.9.10每题7分,共58分)
1、证明:关于x的方程(m2-8m+17)x2+2mx+1=0,不论m取何值,该方程都是一元二次方程.
2、已知关于x的方程x2+x+n=0有两个实数根﹣2,m.求m,n的值.
3、已知关于的一元二次方程有两个不相等的实数根
(1)求的取值围;
(2)若为正整数,且该方程的根都是整数,求的值。
4、已知m是方程x2﹣x﹣2=0的一个实数根,求代数式的值.
5、已知,关于x的方程的两个实数根、满足,数的值.
6、当x满足条件时,求出方程x2﹣2x﹣4=0的根.
.
7、关于的一元二次方程x2+2x+k+1=0的实数解是x1和x2.
(1)求k的取值围;
(2)如果x1+x2﹣x1x2<﹣1且k为整数,求k的值.
.
.
8、关于x的一元二次方程x2+3x+m-1=0的两个实数根分别为x1,x2.
(1)求m的取值围.
(2)若2(x1+x2)+ x1x2+10=0.求m的值.
9、已知关于x的一元二次方程x2+(m+3)x+m+1=0.
(1)求证:无论m取何值,原方程总有两个不相等的实数根:
(2)若x1,x2是原方程的两根,且|x1-x2|=2,求m的值,并求出此时方程的两根.
10、当为何值时,关于的方程有实根。
附加题(15分):
已知是一元二次方程的两个实数根.
(1) 是否存在实数,使成立?若存在,求出的值;若不存在,请您说明理由.
(2) 求使的值为整数的实数的整数值.
.
.
一元二次方程测试题参考答案:
一、填空题:
1、5x2+8x-2=0 5 8 -2 2、2014 3、2 4、-2 5、1或; 6、11 7、m≥0 且m≠1 8、-1 9、2 10、2014 11、3 12、k≤4且k≠0 13、4 14、1 15、-1 16、4 17、①② 18、x2+2x-3=0
19、解:∵a、b是一元二次方程x2-2x-1=0的两个实数根,
∴ab=-1,a+b=2,∴(a-b)(a+b-2)+ab=(a-b)(2-2)+ab=0+ab=-1,故答案为:-1.
20、解:设方程方程x2+(2k+1)x+k2-2=0设其两根为x1,x2,得x1+x2=-(2k+1),x1•x2=k2-2,
△=(2k+1)2-4×(k2-2)=4k+9>0,∴k>-,
∵x12+x22=11,∴(x1+x2)2-2 x1•x2=11,∴(2k+1)2-2(k2-2)=11,解得k=1或-3;∵k>-,故答案为k=1.
21、解:由题意,知当x=2时,分式无意义,∴分母=x2-5x+a=22-5×2+a=-6+a=0,∴a=6;
当x2-5x+a=0时,△=52-4a=25-4a, ∵a<6,∴△>0,
∴方程x2-5x+a=0有两个不相等的实数根,即x有两个不同的值使分式无意义.
故当a<6时,使分式无意义的x的值共有2个.故答案为6,2.
22、解:∵x1、x2是一元二次方程x2+5x﹣3=0的两个实根,
∴x1+x2=﹣5,x1x2=﹣3,x22+5x2=3,
又∵2x1(x22+6x2﹣3)+a=2x1(x22+5x2+x2﹣3)+a=2x1(3+x2﹣3)+a=2x1x2+a=4,
∴﹣10+a=4, 解得:a=14.
23、 24、 25、
二、选择题:
1、B 2、D 3、C 4、B 5、(5) 6、B 7、D
8、解:∵x1和x2为方程的两根,
∴(x1-a)(x1-b)=1且(x2-a)(x2-b)=1,∴(x1-a)和(x1-b)同号且(x2-a)和(x2-b)同号;∵x1<x2,
∴(x1-a)和(x1-b)同为负号而(x2-a)和(x2-b)同为正号,可得:x1-a<0且x1-b<0,x1<a且x1<b, ∴x1<a,∴x2-a>0且x2-b>0, ∴x2>a且x2>b,∴x2>b,
∴综上可知a,b,x1,x2的大小关系为:x1<a<b<x2.故选C.
9、A 10、 11、C 12、A 13、B 14、C
三、计算题:
1、∵m²-8m+17= m²-8m+16+1=(m-4)²+1
∵(m-4)²≥0 ∴(m-4)²+1²>0即m²-8m+17>0∴不论m取何值,该方程都是一元二次方程。
2、
解:∵关于x的方程x2+x+n=0有两个实数根﹣2,m,
∴,解得,,即m,n的值分别是1、﹣2.
3、解析:
.
.
4、解:(1)∵m是方程x2﹣x﹣2=0的根,
∴m2﹣m﹣2=0,m2﹣2=m, ∴原式=(m2﹣m)(+1)=2×(+1)=4.
5、解:原方程可变形为:.
∵、是方程的两个根,∴△≥0,即:4(m +1)2-4m2≥0, ∴ 8m+4≥0, m≥.
又、满足,∴=或=- , 即△=0或+=0,
由△=0,即8m+4=0,得m=.
由+=0,即:2(m+1)=0,得m=-1,(不合题意,舍去),所以,当时,m的值为
6、:解:由求得,则2<x<4.
解方程x2﹣2x﹣4=0可得x1=1+,x2=1﹣,
∵2<<3,∴3<1+<4,符合题意∴x=1+.
7、:解:(1)∵方程有实数根,
∴△=22﹣4(k+1)≥0, 解得k≤0.故K的取值围是k≤0.
(2)根据一元二次方程根与系数的关系,得x1+x2=﹣2,x1x2=k+1
x1+x2﹣x1x2=﹣2﹣(k+1).
由已知,得﹣2﹣(k+1)<﹣1,解得k>﹣2.
又由(1)k≤0,∴﹣2<k≤0.
∵k为整数,∴k的值为﹣1和0.
8、
.
.
解题时,一定要注意其前提是此方程的判别式△≥0
9、解:(1)证明:∵△=(m+3)2-4(m+1)…1分
=(m+1)2+4,∵无论m取何值,(m+1)2+4恒大于0
∴原方程总有两个不相等的实数根。
(2)∵x1,x2是原方程的两根,∴x1+x2=-(m+3),x1•x2=m+1,
∵|x1-x2|=2,∴(x1-x2)2=(2)2,∴(x1+x2)2-4x1x2=8。
∴[-(m+3)]2-4(m+1)=8∴m2+2m-3=0。 解得:m1=-3,m2=1。
当m=-3时,原方程化为:x2-2=0, 解得:x1=,x2=-.
当m=1时,原方程化为:x2+4x+2=0, 解得:x1=-2+,x2=-2-.
10、解:当=0即时,≠0,方程为一元一次方程,总有实根;当≠0即时,方程有根的条件是:
△=≥0,解得≥
∴当≥且时,方程有实根。
综上所述:当≥时,方程有实根。
附加题:解:(1) 假设存在实数,使成立.
∵ 一元二次方程的两个实数根
∴ ,
又是一元二次方程的两个实数根
∴
∴
,但.
∴不存在实数,使成立.
(2) ∵
∴ 要使其值是整数,只需能被4整除,故,注意到,
.
.
要使的值为整数的实数的整数值为.
.
相关文档
- 2018年四川省南充市中考数学试卷含2021-11-0621页
- 2019四川省绵阳中考数学试卷(word版2021-11-0623页
- 2019年四川省内江市中考数学试卷2021-11-0630页
- 2013山东泰安中考数学试题2021-11-0611页
- 2018年山东省聊城市中考数学试卷2021-11-0628页
- 九年级下册数学同步练习32-1 投影 2021-11-062页
- 湘教版九年级数学上册同步测试题课2021-11-0627页
- 2019广东省中考数学试题(word版,含手2021-11-069页
- 人教版9年级下册数学精品示范教案22021-11-062页
- 人教版九年级数学上册第二十一章一2021-11-0622页