鄂尔多斯专版2020中考数学复习方案选择填空限时练03试题 6页

选择填空限时练(三)‎ 限时:35分钟　满分:48分 一、选择题(每小题3分,共30分)‎ ‎1.-27的立方根是 (　　)‎ A.3 B.3‎3‎ ‎ C.-‎1‎‎3‎ D.-3‎ ‎2.斑叶兰被列为国家二级保护植物,它的一粒种子重约0.0000005克.将0.0000005用科学记数法表示为 (　　)‎ A.5×107 B.5×10-7‎ C.0.5×10-6 D.5×10-6‎ ‎3.函数y=x+2‎中,自变量x的取值范围是 (　　)‎ A.x>2 B.x≥-2‎ C.x≤-2 D.x>-2‎ ‎4.下列计算正确的是 (　　)‎ A.a2+a2=2a4 B.3a2b2÷a2b2=3ab ‎ C.(-a2)2=a4 D.(-m3)2=m9‎ ‎5.为得到抛物线y=-6x2,可将抛物线y=-6x2+5 (　　)‎ A.向上平移5个单位 ‎ B.向下平移5个单位 C.向左平移5个单位 ‎ D.向右平移5个单位 ‎6.如图X3-1,某厂生产一种扇形折扇,OB=10 cm,AB=20 cm,其中裱花的部分是用纸糊的.若扇子完全打开摊平时纸面面积为‎1000‎‎3‎π cm2,则扇形圆心角的度数为 (　　)‎ 图X3-1‎ A.120° B.140° ‎ C.150° D.160°‎ 6‎ ‎7.某市为解决部分市民冬季集中取暖问题,需铺设一条长3000米的管道,为尽量减少施工对交通造成的影响,实际施工时……,设实际每天铺设管道x米,则可得方程‎3000‎x-10‎‎-‎‎3000‎x=15,根据此情景,题中用“……”表示的缺失的条件应补为(　　)‎ A.每天比原计划多铺设10米,结果延期15天才完成 B.每天比原计划少铺设10米,结果延期15天才完成 C.每天比原计划多铺设10米,结果提前15天完成 D.每天比原计划少铺设10米,结果提前15天完成 ‎8.给出按一定规律排列的一列数:‎3‎,‎8‎‎2‎,‎15‎‎3‎,‎24‎‎4‎,…,其中第6个数为 (　　)‎ A.‎3‎‎7‎‎7‎ B.‎35‎‎5‎ ‎ C.‎35‎‎6‎ D.‎‎2‎‎3‎‎3‎ ‎9.下列命题:‎ ‎①对角线互相垂直的平行四边形是正方形;②若‎(m-1‎‎)‎‎2‎=m-1,则m≥1;③过弦的中点的直线必经过圆心;④圆的切线垂直于经过切点的半径;⑤圆的两条平行弦所夹的弧相等.其中真命题有 (　　)‎ A.1个 B.2个 ‎ C.3个 D.4个 ‎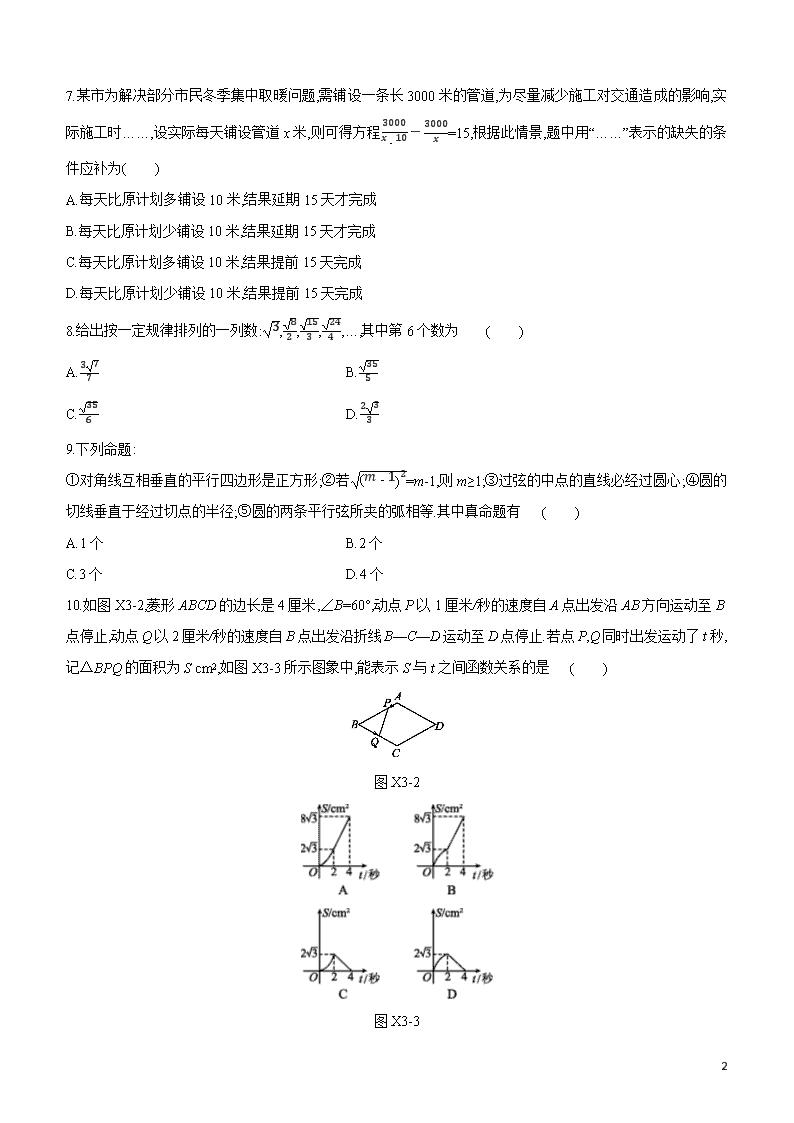10.如图X3-2,菱形ABCD的边长是4厘米,∠B=60°,动点P以1厘米/秒的速度自A点出发沿AB方向运动至B点停止,动点Q以2厘米/秒的速度自B点出发沿折线B—C—D运动至D点停止.若点P,Q同时出发运动了t秒,记△BPQ的面积为S cm2,如图X3-3所示图象中,能表示S与t之间函数关系的是 (　　)‎ 图X3-2‎ 图X3-3‎ 6‎ 二、填空题(每小题3分,共18分)‎ ‎11.已知无理数1+2‎3‎,若a<1+2‎3‎0;‎ ‎③ac-b+1=0;‎ ‎④OA·OB=-ca.‎ 图X3-5‎ 其中正确的结论有　　　　个. ‎ ‎16.如图X3-6,△ABC,△EFG都是边长为2的等边三角形,点D是边BC,EF的中点,直线AG,FC相交于点M,当△EFG绕点D旋转时,线段BM长的最小值是　　　　. ‎ 图X3-6‎ 6‎ 附加训练 ‎ ‎17.计算:4sin60°+(π-1)0-‎12‎+|‎3‎-1|.‎ ‎18.先化简,再求值:x‎2‎x-1‎‎-‎x‎2‎x‎2‎‎-1‎÷x‎2‎‎-xx‎2‎‎-2x+1‎,其中x是不等式组x-3(x-2)≤4,‎‎2x-3‎‎3‎‎<‎‎5-x‎2‎的整数解.‎ 6‎ ‎【参考答案】‎ ‎1.D　2.B　3.B　4.C　5.B　6.C ‎7.C　[解析]实际每天铺设管道x米,方程‎3000‎x-10‎‎-‎‎3000‎x=15,则表示原计划用的时间-实际用的时间=15天,那么就说明实际每天比原计划多铺设10米,结果提前15天完成任务.故选C.‎ ‎8.D　[解析]根据题意可知第n个数为‎(n+1‎)‎‎2‎-1‎n,则第6个数为‎(6+1‎)‎‎2‎-1‎‎6‎‎=‎48‎‎6‎=‎‎2‎‎3‎‎3‎.‎ ‎9.C ‎10.D　[解析]当0≤t≤2时,点Q在BC上,此时BP=4-t,BQ=2t,BQ上的高为BP·sinB,S=‎1‎‎2‎(4-t)·sin60°·2t=-‎3‎‎2‎t2+2‎3‎t,其图象是开口向下的抛物线的一部分,可排除A和C.‎ 当20.‎ ‎∵抛物线与y轴的交点在x轴上方,‎ ‎∴c>0.∴abc<0.∴①正确;‎ ‎∵抛物线与x轴有2个交点,∴Δ=b2-4ac>0.‎ 又a<0,∴b‎2‎‎-4ac‎4a<0.∴②错误;‎ ‎∵C(0,c),OA=OC,∴A(-c,0).‎ 6‎ 把A(-c,0)的坐标代入y=ax2+bx+c,‎ 得ac2-bc+c=0,∴c(ac-b+1)=0,∵c≠0,‎ ‎∴ac-b+1=0.∴③正确;‎ 设A(x1,0),B(x2,0).‎ ‎∵二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,‎ ‎∴x1和x2是方程ax2+bx+c=0(a≠0)的两根,‎ ‎∴x1·x2=ca.∴OA·OB=-ca.∴④正确.‎ ‎16.‎3‎-1　[解析]设O为AC中点,连接AD,DG,BO,OM,‎ 由AD⊥BC,GD⊥EF,DA=DG,DC=DF,‎ 得∠ADG=90°-∠CDG=∠FDC,DADC‎=‎DGDF,‎ 所以△DAG∽△DCF,∠DAG=∠DCF,即D,M点在以AC为直径的圆上,BM的最小值为BO-OM,因为BO=BC‎2‎-OC‎2‎‎=‎2‎‎2‎‎-‎‎1‎‎2‎=‎‎3‎,OM=‎1‎‎2‎AC=1,所以BM的最小值为‎3‎-1.‎ 附加训练 ‎17.解:4sin60°+(π-1)0-‎12‎+|‎3‎-1|‎ ‎=4×‎3‎‎2‎+1-2‎3‎‎+‎‎3‎-1‎ ‎=2‎3‎+1-2‎3‎‎+‎‎3‎-1‎ ‎=‎3‎.‎ ‎18.解:原式=x‎3‎‎+‎x‎2‎‎(x+1)(x-1)‎‎-‎x‎2‎‎(x+1)(x-1)‎·‎‎(x-1‎‎)‎‎2‎x(x-1)‎ ‎=x‎3‎‎(x+1)(x-1)‎·‎‎(x-1‎‎)‎‎2‎x(x-1)‎ ‎=x‎2‎x+1‎,‎ 解不等式组,得1≤x<3,则不等式组的整数解为1,2.‎ 当x=1时,原分式无意义;取x=2,则原式=‎4‎‎3‎.‎ 6‎