2011年东城区初三数学一模试题及答案 12页

北京市东城区2010--2011学年第二学期初三综合练习（一）‎ 数 学 试 卷 考 生 须 知 ‎1.本试卷共5页，共五道大题，25道小题，满分120分.考试时间120分钟.‎ ‎2.在试卷和答题卡上认真填写学校名称、姓名和准考证号.‎ ‎3.试题答案一律填涂或书写在答题卡上，在试卷上作答无效.‎ ‎4.在答题卡上，选择题、作图题用2B铅笔作答，其他试题用黑色字迹签字笔作答.‎ ‎5.考试结束，请将本试卷、答题卡一并交回.‎ 一、选择题（本题共32分，每小题4分）‎ 下面各题均有四个选项，其中只有一个是符合题意的.‎ ‎1.-2的相反数是 ‎ A. 2 B. C. D. -2‎ ‎2.根据国家统计局的公布数据，2010年我国GDP的总量约为398 000亿元人民币. ‎ ‎ 将398 000 用科学记数法表示应为 ‎ A. 398×103 B. 0.398×‎106 C. 3.98×105 D. 3.98×106‎ ‎3．如图，直线AB∥CD，∠A＝70°，∠C＝40°，则∠E等于 ‎ A . 30°　 B. 40°　 C. 60°　 D . 70°‎ ‎4．如图，在△ABC中，D、E分别是BC、AC边的中点．‎ ‎ 若DE=2，则AB的长度是 ‎ A．6 B．5‎ ‎ C．4 D．3‎ ‎5.甲、乙、丙、丁四名学生10次小测验成绩的平均数(单位：分)和方差如下表：‎ 选 手 甲 乙 丙 丁 平均数 ‎92‎ ‎92‎ ‎92‎ ‎92‎ 方差 ‎0.035‎ ‎0.015‎ ‎0.025‎ ‎0.027‎ 则这四人中成绩最稳定的是 A.甲 B.乙 C.丙 D.丁 ‎6．已知圆锥的母线长为4，底面半径为2，则圆锥的侧面积等于 ‎ ‎ A．11 B．‎10‎ C．9 D．8‎ ‎7. 若从10~99这连续90个正整数中选出一个数，其中每个数被选出的机会相等，则选出的 ‎ 数其十位数字与个位数字的和为9的概率是 ‎ A． B. C. D. 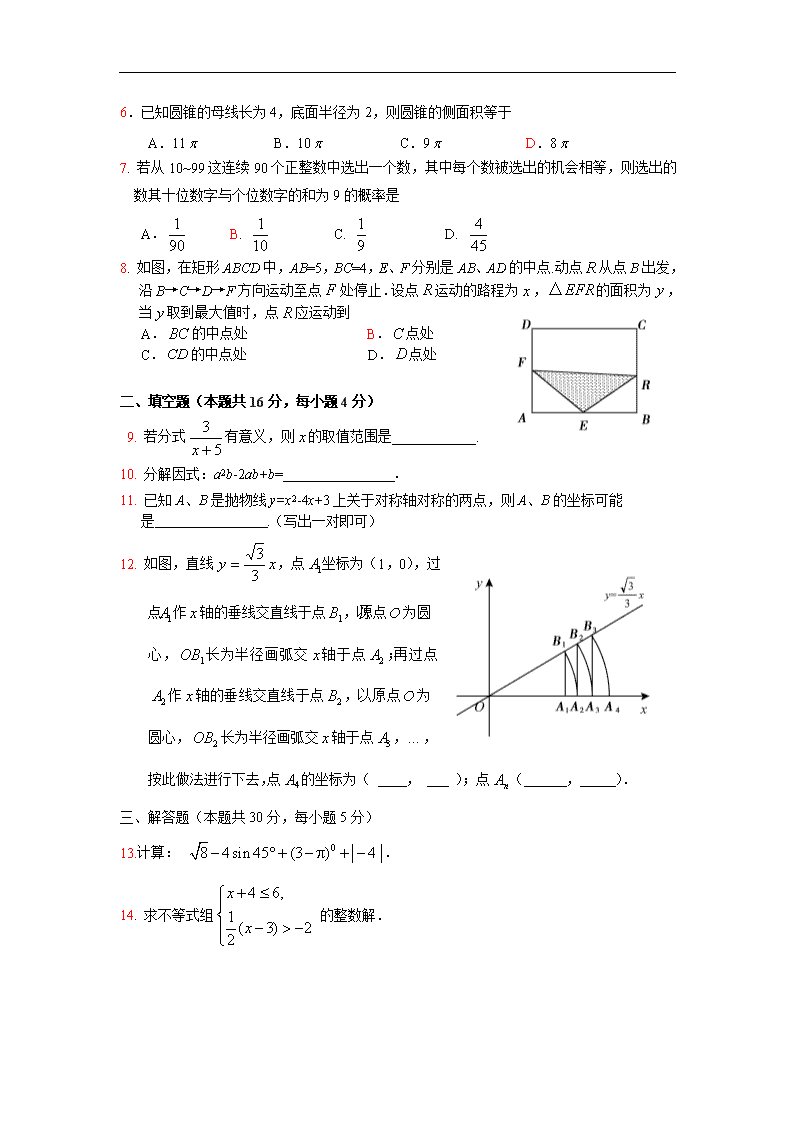‎ ‎8. 如图，在矩形ABCD中，AB=5，BC=4，E、F分别是AB、AD的中点.动点从点B出发，沿B→C→D→F方向运动至点处停止．设点运动的路程为，的面积为，当取到最大值时，点应运动到 ‎ A．的中点处 B．点处 ‎ C．的中点处 D．点处 二、填空题（本题共16分，每小题4分）‎ ‎9. 若分式有意义，则的取值范围是____________.‎ ‎10. 分解因式：a2b-2ab+b=________________.‎ ‎11. 已知A、B是抛物线y=x2-4x+3上关于对称轴对称的两点，则A、B的坐标可能 是 .（写出一对即可）‎ ‎12. 如图，直线，点坐标为（1，0），过点作轴的垂线交直线于点，以原点为圆心，长为半径画弧交轴于点；再过点作轴的垂线交直线于点，以原点为圆心，长为半径画弧交轴于点，…，按此做法进行下去，点的坐标为（ ， ）；点（ ， ）．‎ 三、解答题（本题共30分，每小题5分）‎ ‎13.计算： ．‎ ‎14. 求不等式组 的整数解．‎ ‎15．先化简，再求值：，其中.‎ ‎16. 如图，在四边形ABCD中， AC是∠DAE的平分线，DA∥CE，∠AEB=∠CEB. ‎ 求证：AB=CB. ‎ ‎17.列方程或方程组解应用题 随着人们节能意识的增强，节能产品进入千家万户，今年1月小明家将天燃气热水器换成了太阳能热水器．去年12月份小明家的燃气费是96元，从今年1月份起天燃气价格每立方米上涨25%，小明家2月份的用气量比去年12月份少‎10立方米，2月份的燃气费是90元．问小明家2月份用气多少立方米．‎ ‎18．如图，在平行四边形中，过点A分别作AE⊥BC于点E，AF⊥CD于点F．‎ ‎（1）求证：∠BAE=∠DAF；‎ ‎（2）若AE=4，AF=，，求CF的长．‎ 四、解答题（本题共20分，每小题5分）‎ ‎19. 某中学的地理兴趣小组在本校学生中开展主题为“地震知识知多少”的专题调查活动，采取随机抽样的方式进行问卷调查，问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级，划分等级后的数据整理如下表：‎ 等级 非常了解 比较了解 基本了解 不太了解 频数 ‎40‎ ‎120‎ n ‎4‎ 频率 ‎0.2‎ m ‎0.18‎ ‎0.02‎ ‎（1）表中的m的值为_______，n的值为 ．‎ ‎（2）根据表中的数据，请你计算“非常了解”的频率在下图中所对应的扇形的圆心角的度数，并补全扇形统计图．‎ ‎（3）若该校有1500名学生，请根据调查结果估计这些学生中“比较了解”的人数约为多少？‎ ‎20. 已知：AB是⊙O的弦，OD⊥AB于M交⊙O于点D，CB⊥AB交AD的延长线于C．‎ ‎（1）求证：AD＝DC；‎ ‎（2）过D作⊙O的切线交BC于E，若DE＝2，CE=1，‎ 求⊙O的半径．‎ ‎21．在平面直角坐标系xOy中，一次函数y=kx+b与反比例函数y=的图象交于A(1,6)，B(a,3)两点 .‎ ‎（1）求k， k的值；‎ ‎（2）如图，点D在x轴上，在梯形OBCD中，BC∥OD,OB=DC,过点C作CE⊥OD于点E，CE和反比例函数的图象交于点P，当梯形OBCD的面积为18时，求PE：PC的值.‎ ‎22. 如图1，在△ABC中，已知∠BAC＝45°，AD⊥BC于D，BD＝2，DC＝3，求AD的长. ‎ 小萍同学灵活运用轴对称知识，将图形进行翻折变换如图1.她分别以AB、AC为对称轴，画出△ABD、△ACD的轴对称图形，D点的对称点为E、F，延长EB、FC相交于G点，得到四边形AEGF是正方形.设AD=x，利用勾股定理，建立关于x的方程模型，求出x的值.‎ ‎（1）请你帮小萍求出x的值.‎ ‎(2) 参考小萍的思路，探究并解答新问题：‎ 如图2，在△ABC中，∠BAC＝30°，AD⊥BC于D，AD＝4.请你按照小萍的方法画图,得到四边形AEGF，求△BGC的周长.（画图所用字母与图1中的字母对应）‎ 图1 图2‎ 五、解答题（本题共22分，第23题7分，第24题7分，第25题8分）‎ ‎23. 已知关于x的方程(m-1)x2-(‎2m-1)x+2=0有两个正整数根.‎ ‎(1) 确定整数m值；‎ ‎(2) 在（1）的条件下，利用图象写出方程 ‎(m-1)x2-(‎2m-1)x+2+=0的实数根的个数. ‎ ‎24. 等边△ABC边长为6，P为BC边上一点，∠MPN=60°，且PM、PN分别于边AB、AC交于点E、F.‎ ‎（1）如图1，当点P为BC的三等分点，且PE⊥AB时，判断△EPF的形状；‎ ‎（2）如图2，若点P在BC边上运动，且保持PE⊥AB，设BP=x，四边形AEPF面积的y，求y与x的函数关系式，并写出自变量x的取值范围；‎ ‎（3）如图3，若点P在BC边上运动，且∠MPN绕点P旋转，当CF=AE=2时，求PE的长.‎ 图1 图2 图3‎ ‎25. 如图，已知二次函数y=ax2+bx+8（a≠0）的图像与x轴交于点A（-2，0），B，与y轴交于点C，tan∠ABC=2．‎ ‎（1）求抛物线的解析式及其顶点D的坐标；‎ ‎（2）设直线CD交x轴于点E．在线段OB的垂直平分线上是否存在点P，使得经过点P的直线PM垂直于直线CD，且与直线OP的夹角为75°？若存在，求出点P的坐标；若不存在，请说明理由；‎ ‎（3）过点B作x轴的垂线，交直线CD于点F，将抛物线沿其对称轴向上平移，使抛物线与线段EF总有公共点．试探究：抛物线最多可以向上平移多少个单位长度？‎ 北京市东城区2010--2011学年第二学期初三综合练习（一）‎ 数学试卷参考答案 一、选择题（本题共32分，每小题4分） ‎ 题 号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答 案 A C A C B D ‎ B B 二、填空题（本题共16分，每小题4分）‎ 题 号 ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答 案 x≠5‎ b(a-1)2‎ ‎（1,0），（3,0）或 ‎（0,3），（4,3）等 ‎，0‎ ‎，0‎ 三、解答题：（本题共30分，每小题5分）‎ ‎13．（本小题满分5分）‎ 解: ‎ ‎=+1+4 ………………………………………4分 ‎=5． …………………………………… 5分 ‎14．（本小题满分5分）‎ 解：由①得：x≤2. --------1分 由②得：x-3＞-4,‎ x＞-1. --------2分 ‎0‎ ‎1‎ ‎2‎ ‎-1‎ ‎∴原不等式组的解集为 -1＜x≤2. --------3分 ‎∴原不等式组的整数解为 0,1,2. --------5分 ‎15．（本小题满分5分）‎ ‎=--------2分 ‎=‎ ‎=. --------3分 当时，‎ ‎.--------5分 ‎2‎ ‎3‎ ‎1‎ ‎16．（本小题满分5分）‎ 证明：∵AC是∠DAE的平分线， ‎ ‎ ∴∠1=∠2. -------1分 又∵AD∥EC，‎ ‎∴∠2=∠3. ------2分 ‎∴∠1=∠3.‎ ‎∴AE=CE. --------3分 在△ABE和△CBE中，‎ ‎ AE=CE，‎ ‎∠AEB=∠CEB，‎ BE=BE，‎ ‎∴△ABE≌△CBE. --------4分 ‎∴AB=CB. ------5分 ‎17．（本小题满分5分） ‎ 解：设小明家2月份用气x立方米，则去年12月份用气(x+10) 立方米．-------1分 根据题意，得 ． ----------------3分 解这个方程，得x＝30． ---------------4分 经检验，x＝30是所列方程的根． ‎ 答：小明家2月份用气‎30立方米． -----------------5分 ‎18．（本小题满分5分） ‎ 证明：（1）∵四边形ABCD是平行四边形，‎ ‎∴∠B=∠D.‎ 又AE⊥BC，AF⊥CD，‎ ‎∴∠AEB=∠AFD.‎ ‎∴∠BAE=∠DAF.---------2分 ‎（2）在Rt△ABE中，sin∠BAE=，AE=4,可求 AB=5. ---------3分 又∵∠BAE=∠DAF，‎ ‎∴ sin∠DAF=sin∠BAE=.‎ 在Rt△ADF中，AF=, sin∠DAF =,可求DF=-------4分 ‎∵ CD=AB=5.‎ ‎∴CF=5-=． …………………………………………5分 四、解答题（本题共20分，每小题5分）‎ ‎19.（本小题满分5分）‎ 解：（1）0.6；36；------------2分 ‎（2）72°；补全图如下：‎ ‎------------4分 ‎（3）1500×0.6＝900. ‎ 答：学生中“比较了解”的人数约为900人 ------------5分 ‎20.（本小题满分5分）‎ ‎（1）证明：在⊙O中，OD⊥AB，CB⊥AB，‎ ‎∴AM＝MB，OD∥BC. …………………1分 ‎∴AD＝DC. ……………2分 ‎（2）∵DE为⊙O切线， ‎ ‎∴OD⊥DE ……………3分 ‎ ‎∴四边形MBED为矩形.‎ ‎∴DE∥AB. ……………4分 ‎∴MB=DE=2，MD=BE＝EC=1.‎ 连接OB.‎ 在Rt△OBM中，OB2=OM2+BM2. ‎ 解得 OB= . …………………5分 ‎21．（本小题满分5分）‎ 解：（1）∵点A(1,6),B(a,3)在反比例函数y=的图象上，‎ ‎∴ k=1×6=6. --------1分 ‎∴ a×3=6，a=2.‎ ‎∴B(2，3).‎ 由点A(1,6),B(2,3)也在直线y=kx+b上，‎ 得 ‎ 解得k=-3. ‎ ‎∴k=-3， k=6. -----------------2分 ‎(2) 设点P的坐标为（m,n）. ‎ 依题意，得 ×3（m+2+m-2）=18，m=6. -----------------3分 ‎∴ C（6,3），E（6,0）.‎ ‎∵ 点P在反比例函数y=的图象上， ‎ ‎∴ n=1. ------------------4分 ‎∴PE ：PC=1：2 . ------------------5分 ‎22．（本小题满分5分）‎ 解： （1）设AD=x，由题意得，BG=x－2，CG=x-3.‎ 在Rt△BCG中，由勾股定理可得 .‎ 解得 . --------------2分 ‎ ‎（2）参考小萍的做法得到四边形AEGF，∠EAF=60°，‎ ‎∠EGF=120°，∠AEG=∠AFG= 90°，AE=AF=AD=4.‎ 连结EF，可得 △AEF为等边三角形.‎ ‎∴ EF=4.‎ ‎∴ ∠FEG=∠EFG= 30°.‎ ‎∴ EG=FG. ‎ 在△EFG中，可求，.‎ ‎ ∴△EFG的周长＝BG+CG+BC=BG+CG+EB+FC=2EG=. --------------5分 五、解答题：（本题共22分，第23题7分，第24题7分，第25题8分）‎ ‎23．（本小题满分7分）‎ 解： 由方程(m-1)x2-(‎2m-1)x+2+=0可得 ‎=‎ ‎，‎ ‎∵均为正整数，m也是整数，‎ ‎∴m=2. ----------3分 ‎（2）由（1）知x2-3x+2+=0.‎ ‎∴x2-3x+2= -.‎ 画出函数y= x2-3x+2，y= -的图象，---------6分 由图象可知，两个函数图象的交点个数是1. ---------7分 ‎24. （本小题满分7分）‎ ‎（1）△EPF为等边三角形. --------------1分 ‎（2）设BP=x，则CP＝6－x.‎ ‎ 由题意可 △BEP的面积为.‎ ‎△CFP的面积为.‎ ‎△ABC的面积为.‎ 设四边形AEPF的面积为y.‎ ‎ ∴ =.‎ 自变量x的取值范围为3＜x＜6. --------------4分 ‎（3）可证△EBP∽△PCF.‎ ‎∴ .‎ 设BP=x，‎ 则 .‎ 解得 .‎ ‎∴ PE的长为4或. --------------7分 ‎25．（本小题满分8分）‎ 解：（1）依题意，可知 C(0,8),则B(4,0)‎ 将A(-2,0)，B(4，0)代入 y=ax2+bx+8，‎ ‎ 解得 配方得y，顶点D（1,9）. ---------3分 ‎（2）假设满足条件的点存在，依题意设，‎ 由求得直线的解析式为，‎ 它与轴的夹角为．‎ 过点P作PN⊥y轴于点N.‎ 依题意知，∠NPO=30°或∠NPO=60°.‎ ‎∵PN=2，∴ON= 或2．‎ ‎∴存在满足条件的点，的坐标为（2， ）和(2，2)．-----------6分 ‎（3）由上求得．‎ 当抛物线向上平移时，可设解析式为．‎ 当时，．‎ 当时，．‎ 或．‎ 由题意可得m的范围为．‎ ‎∴ 抛物线最多可向上平移72个单位． -----------8分