浙江省杭州市2020-2021学年上城区开元中学九年级上学期期中数学试卷（PDF版，含答案） 18页

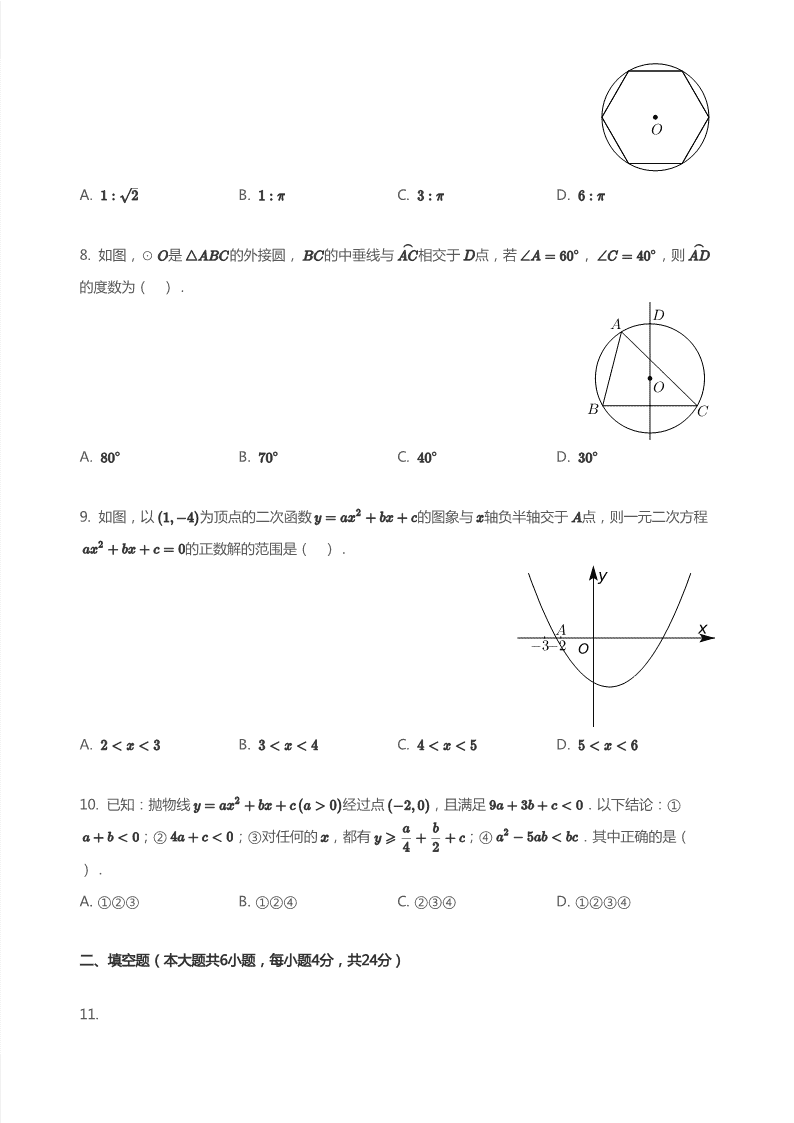
2020~2021学年上城区开元中学初三上学期期中数 学试卷 一、选择题（本大题共10小题，每小题3分，共30分） 1. 下列事件中，为必然事件的是（ ）． A. 明天要下雨 B. C. D. 打开电视机，它正在播广告 A. B. C. D. 2. 在一个不透明的袋中装着 个红球和 个黄球，它们除颜色外其余都相同，随机从袋中摸出 个球， 恰好是红球的概率为（ ）． A. B. C. D. 3. 抛物线 向左平移 个单位，再向上平移 个单位，所得到的抛物线是（ ）． A. 个 B. 个 C. 个 D. 个 4. 抛物线 与 轴的交点个数为（ ）． A. B. C. D. 5. 如图， 是⊙ 的直径， ， ，则 的度数是（ ）． A. B. C. D. 6. 已知圆内接四边形 中， ，则 的大小是（ ）． 7. 圆内接正六边形的边长与该边所对的劣弧的长的比（ ）． A. B. C. D. A. B. C. D. 8. 如图，⊙ 是 的外接圆， 的中垂线与 相交于 点，若 ， ，则 的度数为（ ）． A. B. C. D. 9. 如图，以 为顶点的二次函数 的图象与 轴负半轴交于 点，则一元二次方程 的正数解的范围是（ ）． x y O A. ①②③ B. ①②④ C. ②③④ D. ①②③④ 10. 已知：抛物线 经过点 ，且满足 ．以下结论：① ；② ；③对任何的 ，都有 ；④ ．其中正确的是（ ）． 二、填空题（本大题共6小题，每小题4分，共24分） 11. 一个暗箱里放有 个除颜色外完全相同的球，这 个球中红球只有 个．通过大量重复摸球的实验后发 现，摸到红球的频率稳定在 附近，那么可以推算出 的值大约是 ． 12. 当二次函数 的函数值随 的增大而减小时， 的取值范围是 ． 13. 如图，网格的小正方形的边长均为 ，小正方形的顶点叫做格点， 三个顶点都在格点上，那 么 的外接圆的半径是 ． 14. 已知一个扇形的弧长为 ，圆心角是 ，则它的半径长为 ，扇形的面积为 ． 15. 已知二次函数 ，当自变量 时，则 的取值范围为 ． 16. 如图，在平面直角坐标系中，抛物线 （ 为常数）的顶点为 ，过点 作 轴的平 行线与抛物线 交于点 ，抛物线 的顶点为 ，连结 ， ，则 的面积为 ． 三、解答题（本大题共7小题，共66分） 17. 如图所示， 的各顶点都在 的网格中的格点（即各个小正方形的顶点）上，每个小正方 形的边长都为 ， 绕点 顺时针旋转 得后到的 ． （ 1 ） （ 2 ） 在图中画出 ． 求出在 旋转过程中点 经过的路线长度． （ 1 ） （ 2 ） 18. 小强同学报名参加运动会，有以下 个项目可供选择：径赛项目： ， ， （分别用 、 、 表示）；田赛项目：跳远，跳高（分别用 、 表示）． 小强同学从 个项目中任选一个，恰好是田赛项目的概率为 ． 小强同学从 个项目中任选两个，利用树状图或表格列举出所有可能出现的结果，并求恰好是 一个田赛项目和一个径赛项目的概率． （ 1 ） （ 2 ） 19. 已知抛物线 （ ， 是常数，且 ），过点 ． 求 的值，并通过计算判断点 是否在该抛物线上． 若该抛物线与直线 只有一个交点，求 的值． （ 1 ） （ 2 ） 20. 某农场拟建三间矩形牛饲养室，饲养室的一面全部靠现有墙(墙长为 )，饲养室之间用一道用建 筑材料做的墙隔开(如图)．已知计划中的建筑材料可建围墙的总长为 ，设三间饲养室合计长 ， 总占地面积为 ． 求 关于 的函数表达式和自变量 的取值范围． 为何值时，三间饲养室占地总面积最大？最大为多少？ （ 1 ） （ 2 ） 21. 已知：如图， 是⊙ 的直径，弦 于点 ， 是 上一点， 与 的延长线交于点 ． ， 求证： ． 当 ， 时，求⊙ 的半径． （ 1 ） （ 2 ） （ 3 ） 22. 在平面直角坐标系中，设二次函数 ，其中 ． 若函数 的图象经过点 ，求函数 的函数表达式． 已知点 ， 在该函数图象上，当 时，求 的值． 已知点 和 在函数 的图象上，若 ，求 的取值范围． （ 1 ） （ 2 ） （ 3 ） 23. 已知， 、 是⊙ 的两条弦， ，过圆心 作 于点 ． 如图 ，求证： ． 如图 ，当 、 、 三点在一条直线上时，求 的度数． 如图 ，在（ ）的条件下，点 为劣弧 上一点， ， ，连结 、 交于 点 ，求 和 的长． 解析: 原抛物线的顶点为 向左平移 个单位， 再向上平移 个单位，那么新抛物线的顶点为 ， 可得新抛物线的解析式为： ． 故选 ． 解析: 令 ， ， ∴抛物线 与 轴交点个数为 ， 故选 ． 解析: ∵ 是⊙ 的直径， ， ， ∴ ， ∴ ， ∴ ． 解析: ∵四边形 为圆内接四边形， ∴ ， ， ∵ ， ∴ ， ∵ ， ∴ ， C3. C4. C5. C6. 【答案】 B1. B2. ∴ ． 故选 ． 解析: 正六边形的中心角为 ， 设内接正六边形的圆的半径为 ， 则以圆心，正六边形顶点构成正三角形，边长为 ， 边长所对应的劣弧的弧长为 ， ∴正六边形的边长和边长所对的弧长之比为： ， 故选 ． 解析: 连结 ， ， ， ∵ ， ∴ ， ， ∵ ， ∴ ， ∵ ， ∴ ， ∵ ， ∴ ， ∴ ， ∵ ， ∴ ， ∵ 垂直平分 ， C7. C8. ∴ ， ∴ ． 故选 ． 解析: ∵二次函数 的顶点为( , )， ∴对称轴为 ， 而对称轴左侧图象与 轴交点横坐标的取值范围是 ， ∴右侧交点横坐标的取值范围是 ． 故选 ． 解析: ∵抛物线 经过点 ， ∴ ， ∵ ， 则 ，故①正确； ②∵ ， ， ∴ ， ， 又∵ ， C9. B10. ∴ ，故②正确； ③∵ ， ∴当 时， ， ∴对称轴 ， 即对称轴 ， ∴该抛物线的最小值不会在 时，故③错误； ④∵ ， ∴ ， 则 ， ∵ ， ， ∴ ， ∴ ， ， ∴ ， 即 ， ，故④正确； 故选 ． 解析: 由题意可得， ，解得 ． 故答案为： 个． 解析: 对称轴 ， 二次函数 ，开口向下， 个11. 12. ∴当函数值随 的增大而减小时， 的取值范围内是 ． 解析: 如图，根据三角形的外心是它的三边垂直平分线的焦点，作出 外接圆的圆心 ，再根据勾股定理得 外接圆的半径 ． 解析: ∵二次函数 中 ， ∴抛物线开口向上，有最小值， ∵ ， ∴抛物线的对称轴为 ， ， ∵ ， ∴当 时， ， ∴ ． 解析: ∵抛物线 （ 为常数）的顶点为 ， ∴点 的坐标为 ， ∵抛物线 ， ∴点 的坐标为 ， 令 ，则有 ， 13. ; 14. 15. 16. （ 1 ） （ 2 ） （ 1 ） （ 2 ） ∴点 的坐标为 ， ∴ ， 点 到直线 的距离 ， 的面积 ． 解析: 分别作出点 、 的对应点 、 ， 位置如图所示． 以 经过的路线为以点 为圆， 为半径旋转 所对的弧， 则 ， 在 旋转过程中点 经过的路线长度 ． 解析: ∵ 个项目中田赛项目有 个， ∴该同学从 个项目中任选一个，恰好是田赛项目的概率为： ； 故答案为： ． 画树状图得： ∵共有 种等可能的结果，恰好是一个田赛项目和一个径赛项目的 种情况， ∴恰好是一个田赛项目和一个径赛项目的概率为： ． （ 1 ）画图见解析． （ 2 ） ． 17. （ 1 ） （ 2 ） ． 18. （ 1 ） （ 2 ） 开始 解析: ∵ 过 ， ∴将 代入 ， ∴ ， ∴ 的值为 ， 将 代入 ， 则左边 ，右边 ， ∴左 右 ， ∴ 在抛物线上． ∵该抛物线与直线 只有一个交点， ∴ ， ， ∴ ， ∴ ， ， ∴ ． （ 1 ） ， 在抛物线上． （ 2 ） ． 19. （ 1 ）见解析 （ 2 ）见解析 20. （ 1 ） （ 2 ） （ 1 ） （ 2 ） 解析: 由题意可知，饲养室的宽为 ， 则 ， 自变量 的取值范围为 ． ， 当 时，三间饲养室占地总面积最大，最大为 ． 解析: 连接 ， ∵弦 ， 是⊙ 直径， ∴ ， ∴ ， ∵四边形 是⊙ 内接四边形， ∴ ， ∵ ， ∴ ， ∴ ． 连接 ， 设⊙ 半径为 ，则 ， ∵ ， ， ∴ ， （ 1 ）证明见解析． （ 2 ） ． 21. （ 1 ） （ 2 ） （ 3 ） ∵ ， ∴ ， 在 中， ， ∴ ， ∴⊙ 半径为 ． 解析: ∵函数 的图象经过 ， ∴ ， 解得 或 ， 又因为 ， ∴ ， ∴函数 的函数表达式为 ． ∵点 ，点 在该函数图象上， ∴ ， ， ∵ ， ∴ ， ∴ ， ∴ ， ， ∵ ， ， ∴ ． ∵抛物线的对称轴为直线 ， ∴点 关于对称轴的对称点为 ， 当点 在对称轴左侧时，由 知 ； 当点 在对称轴右侧时，由 知 ． （ 1 ） ． （ 2 ） ． （ 3 ） 或 ． 22. （ 1 ） （ 2 ） （ 3 ） 综上，若 ，则 的取值范围是 或 ． 解析: 连结 ， ∴ ， ∴ ， ∴ ， 在 和 中， ， ∴ ≌ ， ∴ ． ∵ ， ∴ ， ∵ 、 、 三点共线， ∴ ， ∴ 垂直平分 ， ∴ ， ∴ ， ∴ 是等边三角形， ∴ ． 过点 作 交 延长线于 ， （ 1 ）证明见解析． （ 2 ） ． （ 3 ） ， ． 23. ∵ ， ， ∴ ， ∵ ， ∴ ， ∴设 ，则 ， ， ∴ ， ∵ ， ∴ ， 在 中， ， ∴ ， 整理得 ， 解得 ， （舍）， ∴ ， 故 ， ．