江苏南京市秦淮区2020-2021学年九上数学期中试卷&答案（PDF） 13页

【秦淮区数学】2020 九上期中考试试卷+答案 一、选择题（本大题共 6 小题，每小题 2 分，共 12 分。在每小题所给出的四个选项中，恰 有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上） 1、下列方程是一元二次方程的是（ ） A． 2 2 0x   B． 22 0x x  C． 2 2x y  D． 2 1 2x  2、数据 2，5，4， 3 ， 1 的极差是（ ） A．6 B．7 C．8 D．9 3、用配方法解方程 2 2 4 0x x   时，原方程应变形为（ ） A． 21 3x   B． 2+1 =4x C．  21 5x   D． 22 8x   4、已知 1 2x x、 是一元二次方程 2 2 0x ax   的两个根，下列结论正确的是（ ） A． 1 2x x B． 1 2 0x x  C． 1 2 0x x  D． 1 20 0x x ， 5、如图，在正八边形 ABCDEFGH 中，AE 与 BG 交于点 P，则∠APG 的度数为（ ） A．108° B．112.5° C．120° D．135° （第 5 题） （第 6 题） 6、如图，AB 是 O 的直径，BC 是 O 的弦，BC=3．将 BC 沿着 BC 折叠后恰好经过点 O， 则 AB 的长为（ ） A． 2 2 B． 2 3 C．4 D．5 P H D GC F B A E C O A B 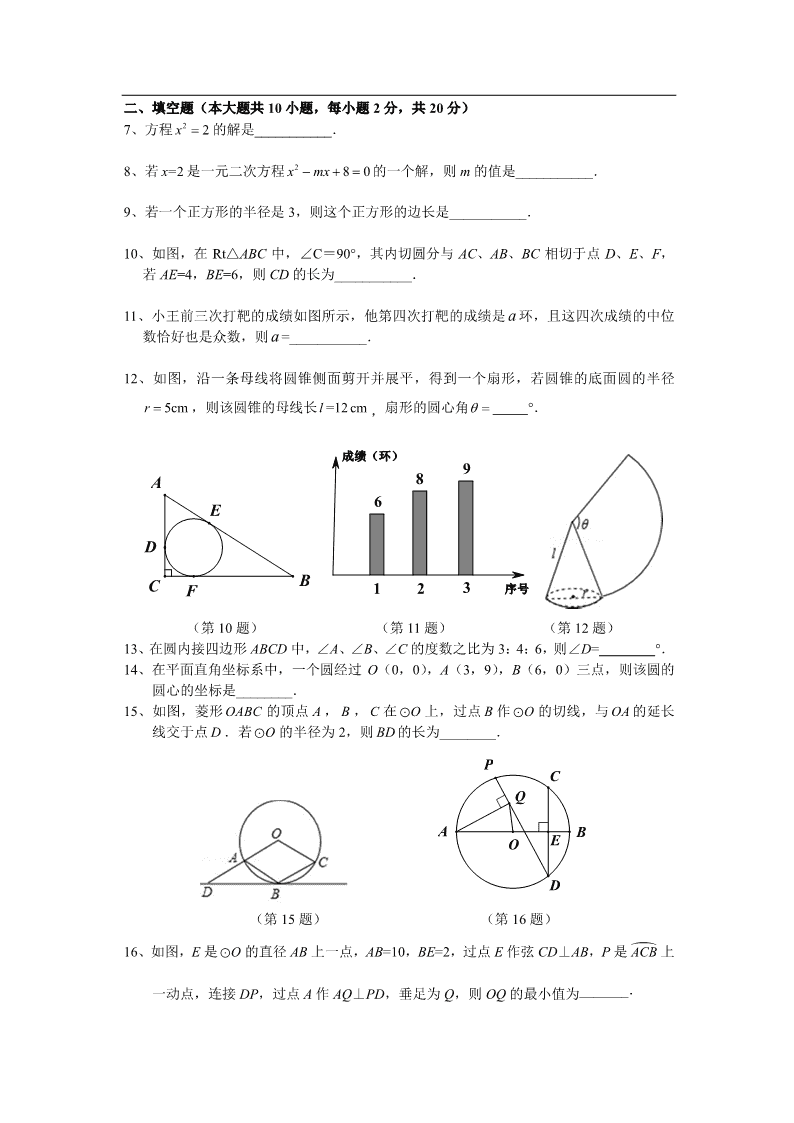二、填空题（本大题共 10 小题，每小题 2 分，共 20 分） 7、方程 2 2x  的解是___________． 8、若 =2x 是一元二次方程 2 8 0x mx   的一个解，则 m 的值是___________． 9、若一个正方形的半径是 3，则这个正方形的边长是___________． 10、如图，在 Rt△ABC 中，∠C＝90°，其内切圆分与 AC、AB、BC 相切于点 D、E、F， 若 AE=4，BE=6，则 CD 的长为___________． 11、小王前三次打靶的成绩如图所示，他第四次打靶的成绩是 a 环，且这四次成绩的中位 数恰好也是众数，则 a =___________． 12、如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形，若圆锥的底面圆的半径 5cmr  ，则该圆锥的母线长l =12cm ，扇形的圆心角  °． （第 10 题） （第 11 题） （第 12 题） 13、在圆内接四边形 ABCD 中，∠A、∠B、∠C 的度数之比为 3：4：6，则∠D= °． 14、在平面直角坐标系中，一个圆经过 O（0，0），A（3，9），B（6，0）三点，则该圆的 圆心的坐标是________． 15、如图，菱形 OABC 的顶点 A ， B ， C 在 O 上，过点 B 作 O 的切线，与 OA 的延长 线交于点 D ．若 O 的半径为 2，则 BD 的长为________． （第 15 题） （第 16 题） 16、如图，E 是 O 的直径 AB 上一点，AB=10，BE=2，过点 E 作弦 CD⊥AB，P 是 ACB 上 一动点，连接 DP，过点 A 作 AQ⊥PD，垂足为 Q，则 OQ 的最小值为_______． F D E A C B 序号 成绩（环） 98 6 321 E Q D O BA CP 三、解答题（本大题共 7 小题，共 88 分. 请在答题卡指定区域内作答，解答时应写出文字 说明、证明过程或演算步骤） 17、（6 分）解方程 2 2 2 0x x   ． 18、（6 分）解方程 2( 1) 5( 1)x x   ． 19、（8 分） ⑴若关于 x 的方程( 3)( 2)x x p   （p 为常数）有两个不相等的实数根，求 p 的取值范围； ⑵关于 x 的方程 2( 3)( +2)x x p  （p 为常数）的根的情况，下列结论中正确的是（ ） （原题是 2( 3)( 2)x x p   ，答案不唯一，我们做了更改） A．两个正根 B．两个负根 C．一个正根，一个负根 D．无实数根 20、（8 分）某商场销售一批衬衫，平均每天可售出 20 件，每件盈利 40 元．为了扩大销售， 增加盈利，商场采取了降价措施．假设在一定范围内，衬衫的单价每降 1 元，商场平均 每天可多售出 2 件，如果降价后商场销售这批衬衫每天盈利 1250 元，那么衬衫的单价降 了多少元？ 21、（8 分）A，B 两家餐饮店规模相当，国庆假期 1~8 日的日盈利情况如图所示． ⑴分别求这两家餐饮店国庆假期的日平均盈利； ⑵若 A，B 两家餐饮店国庆假期的日盈利的方差分别是 2 As 和 2 Bs ，则 2 As 2 Bs ． (填“＞”、“ = ”、“＜”) 22、（6 分）如图，在 ABC△ 中， =AB AC ，点 A 在以 BC 为直径的半圆外，请用无刻度．．．的． 直尺．．画出半圆的圆心O （保留画图痕迹，不写画法）． （第 22 题） A,B两家餐饮店国庆假期1~8日盈利折线统计图 A餐饮店 B餐饮店 2.2 3 5.6 6.57.6 8 7.8 8.2 7.8 9 8.6 9.2 8.8 7 2.4 1.5 10 9 8 7 6 1 5 4 3 2 0 3 4 5 6 7 821 日期 日盈利（万元） 23、（8 分）如图为一个摩天轮示意图．该摩天轮的圆半径为 4.8m，摩天轮上最低点 A 与地 面的距离为 0.8m（即 AC =0.8m）．摩天轮绕点O 逆时针旋转 ts 后，点 A 转动到点 B ， 旋转角为 θ°（0≤θ≤360）．已知摩天轮 60s 转动一周． ⑴θ 与t 之间的函数表达式是__________； ⑵当 t=22.5 时，求点 A 的运动路径长和点 B 与地面的距离． （第 23 题） 24、（10 分）阅读下面解方程的途径． ⑴按照上述途径，填写下面的空格. ⑵已知关于 x 的方程 2 0ax bx c   的解是 1 1x  ， 2 2x  （a、b 、c 均为常数），求关 于 x 的方程 2( ) ( ) 0a kx m b kx m c     （ k 、m 为常数， 0k  ）的解（用含 k 、m 的 代数式表示）． θ° A O B 解方程 解方程 ____②____ ____③____ 方程 的解是 方程 的解是___①____ 25、（8 分）如图， AB 是 O 的弦，点 C 在过点 B 的切线上，且OC OA⊥ ，OC 交 AB 于点 P ． ⑴求证 1=2 A∠ ∠ ； ⑵若 =2PC OP ， = 5AP ，则 O 的半径长为__________． （第 25 题） 26、（10 分）某企业今年 1 月份生产甲、乙、丙三种不同类型的口罩共 70 万个，其中甲种 口罩的产量是乙种口罩的 2 倍，乙种口罩比丙种口罩多 10 万个．为了应对“新冠”疫情， 该企业决定迅速扩大产能，在接下来的两个月中，乙种口罩产量的月平均增长率比甲 种口罩产量的月平均增长率小 1，丙种口罩产量的月平均增长率是甲种口罩产量的月平 均增长率的 2 倍．3 月份该企业口罩总产量是 690 万个． ⑴1 月份该企业分别生产甲、乙、丙三种口罩 万个、 万个、 万个； ⑵求甲种口罩产量的月平均增长率． 27、（10 分）半圆 O 的直径 8AB  ，C 为半圆上一点． ⑴若 6AC  ，则 BC 的长是 ； ⑵①如图①，若 D 是 AC 的中点，且 2AD  ，求 BC 的长； ②如图②，若 D、E 是 AC 的三等分点，且 2AD  ，直接写出 BC 的长． D OA B C CE O BA D 【秦淮区数学】2020 九上期中考试答案 一、选择题（本大题共 6 小题，每小题 2 分，共 12 分。在每小题所给出的四个选项中，恰 有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上） 题号 1 2 3 4 5 6 答案 B C C A B B 第 6 题解析: 如图，过 O 做 OH⊥BC 交 BC 于点 H， ∵弧 BC 沿 BC 翻折过圆心， ∴ 1 2OH OB ， ∴∠OBH=30°， ∵BC=3， ∴ 1 3 2 2BH BC  , 在 Rt△OBH 中， 2 2 2OH BH OB  ∴ 3OB  ∴AB=2OB= 2 3 . 二、填空题（本大题共 10 小题，每小题 2 分，共 20 分. 不需写出解答过程，请把答案直 接填写在答题卡相应的位置上．．．．．．．．．） 第 16 题解析： ∵ AQ PD⊥ ， ∴∠AQD=90°. ∴点 Q 在以 AD 为直径的圆上， 取 AD 中点 M，则 M 为圆心， ∵点 P 是弧 ACB 上的动点， ∴点 Q 在弧 AED 上， 连接 MO 并延长，射线 MO 与圆交于点 Q， 此时 OQ 有最小值. ∵AB=10，BE=2， ∴AE=8，OE=3， 连接 OD， ∵CD⊥AB， ∴∠OED=90°， 题号 7 8 9 10 11 答案 1 22 2x x  ， 6 3 2 2 8 题号 12 13 14 15 16 答案 150 100 （3，4） 2 3 5 C OA B Q D C OA B P 在 Rt△OED 中，OD=5， ∴ED＝4， 在 Rt△AED 中，AD= 4 5 ， ∴ 1 2 52MQ AD  ， 在 Rt△AMO 中，OM= 5 ， ∴ 5OQ MQ MO   . 三、解答题（本大题共 11 小题，共 68 分. 请在答题卡指定区域内作答，解答时应写出文字 说明、证明过程或演算步骤） 17、解： 2 2 2x x  2 2 1 2 1x x     21 3x   1 3x    1 1 3x   ， 2 1 3x   18、解：   21 5 +1 =0x x    +1 +1 5 =0x x    +1 4 =0x x  1 1x   ， 2 4x  19、解：⑴ ( 3)( 2)x x p   整理得： 2 5 6 0x x p    ∴ 1a  5b   6c p  ∴ 2 4b ac = 1 4p ∵方程有两个不相等的实数根 ∴ 2 4 0b ac  即1 4p >0 解得： 1 4p   ⑵C 解析： 2( 3)( +2)x x p  整理得： 2 26 0x x p    ∴ 2 4b ac = 225 4p >0 ∴方程有两个不相等的实数根 设方程两根为 1x 、 2x ∵ 1x 2x = 26 p  <0 ∴方程有一个正根，一个负根，故选 C. 20、解：设衬衫的单价降了 x 元 由题意得：  40 20+2 1250x x  2 30 225 0x x    215 0x   1 2 15x x  答：衬衫的单价降了 15 元. 21、⑴ 2.4+8.8+8.6+7.8+8.2+7.6+5.6+3 6.58Ax   1.5+7+9.2+9+7.8+8+6.5+2.2 6.48Bx   ⑵< 22、解：如图所示，点O 即为所求 23、解： ⑴θ=6t ⑵θ=6×22.5°=135° ∴点 A 的运动路径长为135 4.8=3.6180   过点 B 作 BD 垂直于地面，垂足为 D 过点O 作OE BD⊥ ，垂足为 E ∴ = =OCD CDE OED∠ ∠ ∠ =90° ∴四边形OCDE 为矩形 ∴ OEB∠ =90°， =OC ED ∴ BOE∠ =45° ∴ =OE BE 由勾股定理得 2 2 2+ =OE BE OB ∴ 12= 2 5 BE ∴ 12 2+28= + = 5 BD BE DE 24、解： ⑴① 1 2=0 = 1x x，  ② 1=0x  或 1= 1x   ③ 1 2=1 =0x x， ⑵由题意得 + =1kx m 或 + =2kx m 解得 1 2 1 2= =m mx xk k ，  25、解： ⑴证明： ∵OC OA⊥ ∴ AOC∠ =90° ∵ BC 与 O 相切于点 B ∴ OBC∠ =90° ∴ BOC∠ =90°- 1∠ ∵ =OA OB ∴ =A OBA∠ ∠ 在 OAB△ 中， + +A OBA AOB∠ ∠ ∠ =180° ∴ 2 +A∠ 90° + BOC∠ =180° ∴ 2 +A∠ 90°+90°- 1∠ =180° ∴ 1=2 A∠ ∠ ⑵ 5 6 6 解析： ∵ = =BPC APO∠ ∠ 90°- A∠ =CBP∠ 90°- ABO∠ =A ABO∠ ∠ ∴ =BPC CBP∠ ∠ ∴ =CP BC 设 = =2CP BC a ，则 =OP a ∴ =3OC a 由勾股定理得 2 2= - = 5OB OC BC a ∵ 2 2 2= +AP AO PO ∴ 2 2 2( 5) =( 5 ) +a a ∴ 5 6= 5 = 6 r a 26、⑴设 1 月份生产丙种口罩 x 万个， 由题意得： 2( 10) ( 10) 70x x x     解得： 10x  ， 则甲种口罩数量 2( 10) 40x   万个， 乙种口罩数量 10 20x   万个， 丙种口罩数量 10x  万个． ⑵设甲种口罩产量的月平均增长率为 x， 由题意得： 2 2 240(1 ) 20(1 1) 10(1 2 ) 690x x x       解得： 1 16 5x   （舍去）， 2 2x  答：甲种口罩产量的月平均增长率为 200%． 27、⑴ 2 7 ⑵①连接 OD、OC、AC，记 AC 与 OD 的交点为 H， 则 4OA OD OC   ， ∵D 是 AC 的中点， ∴  CD AD ， ∴ 2CD AD  ， 又∵OC OA ， ∴OD 垂直平分 AC， 设 DH x ，则 4OH x  ， ∵CH⊥DO， ∴ 90CHD CHO     ， ∴ 2 2 2 2 2CD DH CH CO OH    ， ∴ 2 2 2 22 4 (4 )x x    ， 解得： 1 2x  ， ∴ 2 2 2 21 152 ( )2 2CH CD DH     ， ∵OD 垂直平分 AC， ∴ 2 15AC CH  ， ∵AB 为⊙O 直径， ∴ 90ACB   ， ∴ 2 2 2 28 ( 15) 7BC AB AC     ． H D O BA C ②连接 AE，由① 15AE  ， ∵D、E 是 AC 的三等分点， ∴   AD DE EC  ， ∴ 2EC DE AD   ， DEA CAE   ， ∴DE∥AC， 作 AH⊥直线 DE 于 H， 作 CI⊥直线 DE 于 I， 则 90H I     ， ∵DE∥AC， ∴ 180 90HAC H       ， ∴四边形 AHIC 是矩形， ∴ AH CI ， HI AC ， 又∵ AD CE ， 90H I     ∴Rt△AHD≌Rt△CIE(HL)， ∴ EI DH ， 设 DH x ，则 2HE x  ， ∵ 90H   ， ∴ 2 2 2 2 2AE HE AH AD DH    ， ∴ 2 2 2 2( 15) ( 2) 2x x    ， 解得： 7 4x  ， ∴ 7 4EI DH  ， ∴ 7 7 1124 4 2HI DH DE EI       ， ∴ 11 2AC HI  ， ∵AB 为⊙O 直径， ∴ 90ACB   ， ∴ 2 2 2 211 3 158 ( )2 2BC AB AC     ． I H CE OA B D