中考数学全程复习方略微专题六相似三角形的基本类型课件 32页

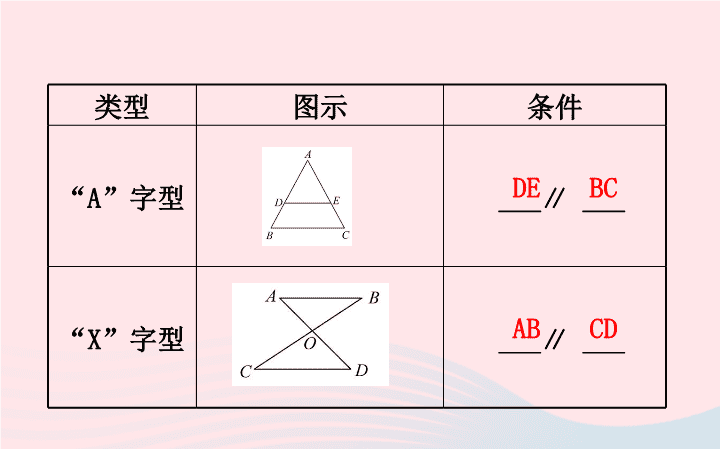
微专题六　 相似三角形的基本类型 【 主干必备 】 常见相似三角形的基本类型 类型 图示 条件 “A” 字型 ___∥ ___ “X” 字型 ___∥ ___ DE BC AB CD 类型 图示 条件 斜交型 ∠AED=∠B 或 _____________ 蝴蝶型 ∠A=∠D 或 _________  ∠ADE=∠C ∠B=∠C 类型 图示 条件 双垂型 AB⊥AC 且 _____________  子母型 ∠CAD= __________  AD⊥BC ∠B 类型 图示 条件 旋转型 ∠BAD=∠CAE 且∠ B= _______________ 或 ∠ BAD=∠CAE 且 ______    “K” 字型 AC⊥_________, DE⊥_________, AB⊥_________  ∠ADE(∠C=∠E) CD CD BE 【 微点警示 】 1. 注意“ A” 字型和斜交型的区别 : 前者有平行 , 后者无平行 . 2. 注意“ X” 字型和蝴蝶型的区别 : 前者有平行 , 后者无平行 . 3. 注意双垂型和子母型的区别 : 前者有垂直 , 后者无垂直 . 【 核心突破 】 【 类型一 】 运用基本类型的相似三 角形计算或证明 例 1(2019· 德州模拟 ) 已知 : 如图 , 在△ ABC 中 , 点 D,E 分别在边 BC,AC 上 , 点 F 在 DE 的延长线 上 ,AD=AF,AE·CE=DE·EF. (1) 求证 :△ADE∽△ACD. (2) 如果 AE·BD=EF·AF, 求证 :AB=AC. 【 思路点拨 】 (1) 由 AE·CE=DE·EF, 推出△ AEF∽△DEC, 可得∠ F=∠C, 再证明∠ ADF=∠C, 即可解决问题 . (2) 欲证明 AB=AC, 利用相似三角形的性质证明∠ B=∠C 即可 . 【 自主解答 】 (1) ∵ AD=AF, ∴ ∠ADF=∠F, ∵ AE·CE=DE·EF, 又 ∵∠ AEF=∠DEC, ∴△AEF∽△DEC, ∴∠F=∠C, ∴∠ADF=∠C, 又∵∠ DAE=∠CAD, ∴△ADE∽△ACD. (2) 略 【 类型二 】 作辅助线构造基本类型的相似三角形 例 2(2019· 安徽中考 ) 如图 , 在 Rt△ABC 中 ,∠ACB=90°,AC=6,BC=12, 点 D 在边 BC 上 , 点 E 在线段 AD 上 ,EF⊥AC 于点 F,EG⊥EF 交 AB 于点 G. 若 EF=EG, 则 CD 的长为 ( 　 　 ) A.3.6 　　　 B.4 　　　 C.4.8 　　　 D.5 B 【 类型三 】 基本类型的相似三角形与四边形综合 例 3(2018· 上海中考 ) 已知 : 如图 , 正方形 ABCD 中 ,P 是边 BC 上一点 ,BE⊥AP,DF⊥AP, 垂足分别是点 E,F. (1) 求证 :EF=AE-BE. (2) 连接 BF, 如果 . 求证 :EF=EP. 【 思路点拨 】 (1) 利用正方形的性质得 AB=AD,∠BAD= 90 ° , 根据等角的余角相等得到∠ BAE=∠ADF, 则可判 断△ ABE≌△DAF, 则 BE=AF, 然后利用等线段代换可得 到结论 . (2) 利用 和 AF=BE 得到 , 则可判定 Rt△BEF∽Rt△DFA, 所以∠ EBF=∠ADF, 再证明∠ EBF= ∠EBP, 即可判断 EF=EP. 【 自主解答 】 略 【 类型四 】 基本类型的相似三角形与圆综合 例 4(2019· 黄冈中考 ) 如图 , 在 Rt△ABC 中 ,∠ACB=90°, 以 AC 为直径的☉ O 交 AB 于点 D, 过点 D 作☉ O 的切线交 BC 于点 E, 连接 OE. (1) 求证 :△DBE 是等腰三角形 . (2) 求证 :△COE∽△CAB. 【 思路点拨 】 (1) 连接 OD, 由 DE 是 ☉ O 的切线 , 得出∠ ODE=90 ° ,∠ADO+∠BDE=90 ° , 由∠ ACB=90 ° , 得出∠ CAB+∠CBA=90 ° , 证出∠ CAB=∠ADO, 得出∠ BDE=∠CBA, 即可得出结论 . (2) 证出 CB 是☉ O 的切线 , 得出 DE=EC, 推出 EC=EB, 再由 OA=OC, 得出 OE∥AB, 即可得出结论 . 【 自主解答 】 (1) 略 (2) ∵ ∠ACB=90 ° ,AC 是☉ O 的直径 , ∴ CB 是☉ O 的切线 , ∵ DE 是☉ O 的切线 , ∴ DE=EC, ∵ EB=ED, ∴ EC=EB, ∵ OA=OC, ∴ OE∥AB, ∴ △COE∽△CAB. 【 明 · 技法 】 从复杂图形中分解 ( 构造 ) 出基本相似三角形的技巧 (1) 见到线段比 , 一般需要作辅助线构造“ A” 字型或“ X” 字型相似三角形 . (2) 见到平行四边形中 , 其中蕴藏着“ A” 字型或“ X” 字型相似三角形 . (3) 见到圆肯定用到相等的圆周角 , 能构造多种类型的相似三角形 . (4) 见到旋转 , 对应边成比例自然形成旋转型相似三角形 . (5) 见到平面直角坐标系 , 通过作垂线往往形成“ K” 字型相似三角形 . 【 题组过关 】 1.(2019· 贺州中考 ) 如图 , 在△ ABC 中 ,D,E 分别是 AB,AC 边上的点 ,DE∥ BC, 若 AD=2,AB=3,DE=4, 则 BC 等于 ( 　 　 ) A.5 　　　　 B.6 　　　　 C.7 　　　　 D.8 B 2.(2019· 日照莒县质检 ) 如图 ,☉O 中弦 AB,CD 相交于点 P, 已知 AP=3,BP=2,CP=1, 则 DP=________.  6 3.(2019· 滨州中考 ) 如图 , ▱ ABCD 的 对角线 AC,BD 交于点 O,CE 平分∠ BCD 交 AB 于点 E, 交 BD 于点 F, 且∠ ABC=60°,AB=2BC, 连接 OE. 下列结论 :①EO⊥AC;②S △AOD =4S △OCF ;③AC∶BD= ∶7; ④FB 2 =OF·DF. 其中正确的结论有 _____________.( 填 写所有正确结论的序号 ) 世纪金榜导学号  ①③④ 4.( 对比分析题 ) 如图 1, 在正方形 ABCD 中 ,E 是边 BC 的中点 ,F 是 CD 上一点 , 已知∠ AEF=90°. (1) 求证 : . (2) 平行四边形 ABCD 中 ,E 是边 BC 上一点 ,F 是边 CD 上一 点 ,∠AFE=∠ADC,∠AEF=90°. 如图 2, 若∠ AFE=45°, 求 的值 . 【 解析 】 (1) 如题干图 1 中 , 设正方形的边长为 2a. ∵ 四边形 ABCD 是正方形 , ∴ ∠B=∠C=90 ° , ∵ ∠AEF=90 ° , ∴ ∠AEB+∠FEC=90 ° ,∠FEC+∠EFC=90 ° , ∴ ∠AEB=∠EFC, ∴ △ABE∽△ECF, ∴ , ∵ BE=EC=a,AB=CD=2a, ∴ CF= a,DF=CD-CF= , (2) 略