2010年石景山区中考二模数学试题答案 5页

‎2010年石景山区中考二模数学试题答案 阅卷须知：‎ 为了阅卷方便，解答题中的推导步骤写得较为详细，考生只要写明主要过程即可．若考生的解法与本解法不同，正确者可参照评分参考给分，解答右端所注分数，表示考生正确做到这一步应得的累加分数．‎ 一、选择题（本题共32分，每小题4分）‎ 题 号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答 案 A B ‎ A ‎ B ‎ B D C C 二、填空题（本题共16分，每小题4分）‎ ‎9．2； 10．； 11．； 12．2．‎ 三、解答题（本题共30分，每小题5分）‎ ‎13．解：原式= …………………………4分 ‎= …………………………………5分 ‎14．解：去分母得： ……………………2分 解得： ………………………………4分 经检验是原方程得根 ………………………………5分 ‎∴原方程得根是 ‎15．证明： ∵CF∥AB ∴ ……………………… 1分 ‎∵是边中点 ∴ ……………………… 2分 ‎∵在△和△中 ‎ ‎ ‎ ∴△≌△ ………………………………… 4分 ‎∴ CF=AD ……………………………………………… 5分 ‎16．解：由得…………………………………………2分 原式 …………………………………………………4分 当时， ‎ ‎ 原式 ………………………………………………5分 ‎17．解：（1）点B1的坐标：_(1,1)_； ………………………………………1分 ‎（2）由题意：A2（-1，1），C2（1，-3）…………………………………3分 设直线A‎2C2的解析式为：‎ ‎∴ 得： ………………………………………5分 ‎∴直线A‎2C2的解析式为：‎ ‎18．解：设集装箱重3吨有x个，重1吨的有个 ………………1分 据题意： …………………………3分 解得：， ……………………………………………4分 答：集装箱重3吨有5个，重1吨的有10个。 …………………………5分 四、解答题（本题共20分，每小题5分）‎ ‎19． 解：如图，过作//交CD于,过A作⊥于 …………1分 E F ‎∴，,AF=DE ……2分 ‎△中，……………3分 ‎△中 ‎ ‎……………………………………4分 ‎∴ ……………………………………5分 ‎20. 解：(1) 小明每周用于健身的时间小时………………………1分 ‎(2）小明每周打球时间=小时，游泳时间=小时 扇形统计图中；表示游泳的扇形圆心角 ……………3分 ‎(3) 答案略 ……………4分 (4) 答案略 ……………………5分 ‎21.（1）证明：联结OD ‎ ‎∵DE是⊙O的切线∴OD⊥DE ……………… ……1分 ‎∵OA=OD ∴∠A=∠ADO ‎∵BA=BC ∴∠A=∠C ‎ ‎∴∠ADO=∠C ‎∴DO∥BC ‎ ‎∴ DE⊥BC …………… ……………2分 ‎（2）解：联结BD ‎∵AB为⊙O的直径 ‎∴∠ADB=90° ……………………………………………………3分 又∵ BA=BC ‎∴AD=DC ‎∴△CDB与△ADB关于BD轴对称 FB=BE=2 ……………………………………………………4分 Rt△DFB中，‎ ‎∠FDB=‎ ‎∴DG=2DF= ……………………………………5分 ‎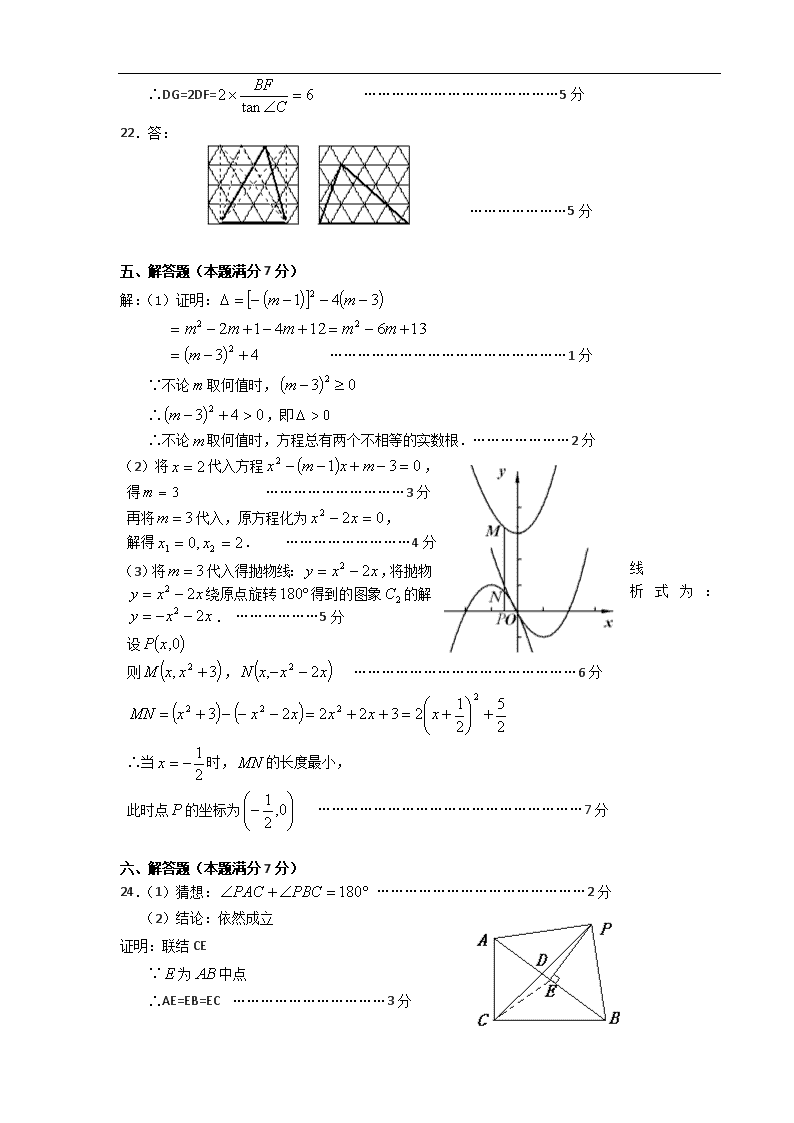22．答：‎ ‎…………………5分 五、解答题（本题满分7分）‎ 解：（1）证明：‎ ‎ ‎ ‎ ……………………………………………1分 ‎∵不论取何值时，‎ ‎∴，即 ‎∴不论取何值时，方程总有两个不相等的实数根．…………………2分 ‎（2）将代入方程，‎ 得 …………………………3分 再将代入，原方程化为，‎ 解得． ………………………4分 ‎（3）将代入得抛物线：，将抛物线绕原点旋转得到的图象的解析式为：． ………………5分 设 则， …………………………………………6分 ‎∴当时，的长度最小，‎ 此时点的坐标为 …………………………………………………7分 ‎ 六、解答题（本题满分7分）‎ ‎24．（1）猜想： ………………………………………2分 ‎（2）结论：依然成立 证明：联结CE ‎∵为中点 ‎∴AE=EB=EC ……………………………3分 ‎∴∠EAC=∠ECA, ‎ ‎∠DCE=∠ECA－∠DCA=∠EAC－45°‎ 又∠DAC=180°－∠ADC－45°=135°－∠PDE …………………………4分 ‎∴∠DCE=135°－∠PDE －45°=90°－∠PDE=∠DPE ‎∴PE=EC=AE …………………………5分 ‎∴△PAE与△PBE为等腰直角三角形，∠APB=90° ………………6分=360°－∠APB－∠ACB=360°－90°－90°=180°……7分 七、解答题（本题满分8分）‎ ‎25． 解：（1）将代入，‎ 得 则抛物线解析式为……………………………1分 直线的解析式为 ……………………………2分 得：， ‎ y D B C ‎（2） 如图，设点的横坐标为，‎ E A 则点的纵坐标为．‎ ‎0‎ x 过点作轴的平行线交于．‎ ‎∴点的坐标为 ‎∴．‎ ‎∴．‎ 解得，∴，……………………………4分 ‎（3）存在符合条件的点共有3个．以下分三类情形探求．‎ 由，，，可得轴，‎ 设直线与轴交于，与交于．‎ 过点作⊥轴于 ，易得，，， ‎ ‎……………………………5分 y ‎① 以为腰且顶角为∠：△．‎ Ｋ Ｍ B C ‎∴ ‎ Ｎ Ｑ O x A 在△ 中，‎ ‎ ∴或 ………………………6分 ‎② 以为腰且顶角为∠：△ ．‎ 在△中，‎ ‎ ∴ 或 ………………………7分 ‎③ 以为底，顶角为∠的△有1个，即 △．‎ 画的垂直平分线交抛物线对称轴于，此时平分线必过等腰△ 的顶点．‎ 过点作垂直轴，垂足为，显然△∽△．‎ ‎∴ ．‎ ‎ ∵ ，∴, 于是 ∴，而在线段上，构不成三角形，舍去。 ……………………8分 综上，符合条件的点共有4个，分别为：‎ ‎，，，．‎