锐角三角函数：余弦、正切2 3页

‎ ‎ ‎28.1 锐角三角形 第二课时 教学目标：‎ 知识与技能：‎ ‎1、了解锐角三角函数的概念，能够正确应用sinA、cosA、tanA表示直角三角形中两边的比．‎ ‎2、逐步培养学生观察、比较、分析、概括的思维能力．‎ 过程与方法：‎ 通过锐角三角函数的学习，进一步认识函数，体会函数的变化与对应的思想，逐步培养学生会观察、比较、分析、概括等逻辑思维能力．‎ 情感态度与价值观：‎ 引导学生探索、发现，以培养学生独立思考、勇于创新的精神和良好的学习习惯．‎ 重难点：‎ ‎1．理解余弦、正切的概念．‎ ‎2．难点：熟练运用锐角三角函数的概念进行有关计算．‎ 教学过程：‎ 一、复习旧知、引入新课 ‎【复习】‎ ‎1、口述正弦的定义 ‎2、（1）如图，已知AB是⊙O的直径，点C、D在⊙O上，且AB＝5，BC＝3．则sin∠BAC= ；sin∠ADC= ．‎ ‎（2）如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于点D。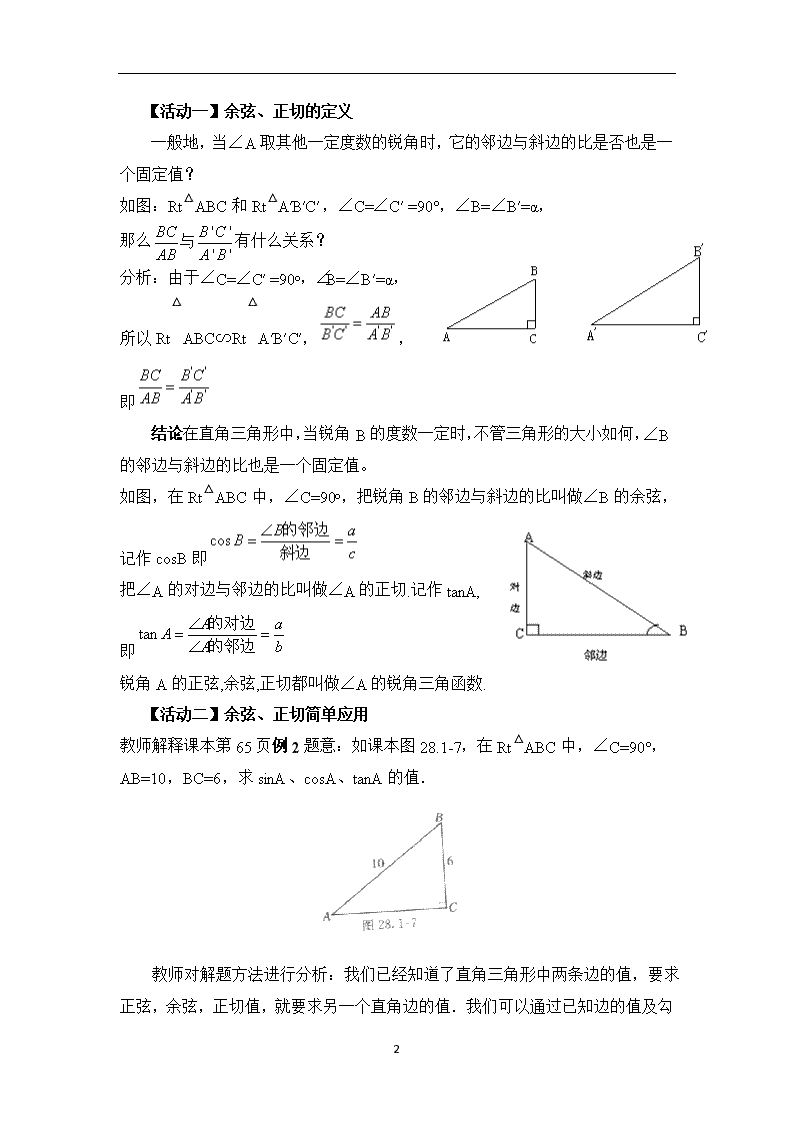已知AC=，BC=2，那么sin∠ACD＝（ ）‎ A． B． C． D．‎ 二、探索新知、分类应用 3‎ ‎ ‎ ‎【活动一】余弦、正切的定义 一般地，当∠A取其他一定度数的锐角时，它的邻边与斜边的比是否也是一个固定值？‎ 如图：Rt△ABC和Rt△A′B′C′，∠C=∠C′ =90°，∠B=∠B′=α，‎ 那么有什么关系？‎ 分析：由于∠C=∠C′ =90o，∠B=∠B′=α，‎ 所以Rt△ABC∽Rt△A′B′C′，，即 ‎ 结论：在直角三角形中，当锐角B的度数一定时，不管三角形的大小如何，∠B的邻边与斜边的比也是一个固定值。‎ 如图，在Rt△ABC中，∠C=90o，把锐角B的邻边与斜边的比叫做∠B的余弦，记作cosB即 把∠A的对边与邻边的比叫做∠A的正切.记作tanA,即 锐角A的正弦,余弦,正切都叫做∠A的锐角三角函数.‎ ‎【活动二】余弦、正切简单应用 教师解释课本第65页例2题意：如课本图28.1-7，在Rt△ABC中，∠C=90°，AB=10，BC=6，求sinA、cosA、tanA的值．‎ ‎ ‎ 3‎ ‎ ‎ 教师对解题方法进行分析：我们已经知道了直角三角形中两条边的值，要求正弦，余弦，正切值，就要求另一个直角边的值．我们可以通过已知边的值及勾股定理来求．‎ ‎ 教师分析完后要求学生自己解题．学生解后教师总结并板书．‎ 三、总结消化、整理笔记 在直角三角形中，当锐角A的大小确定时，∠A的邻边与斜边的比叫做∠A的余弦，记作cosA，把∠A的对边与斜边的比叫做∠A的正切，记作tanA．‎ 四、书写作业、巩固提高 学生做课本第65页练习1、2、3题．分层作业 五、教学后记 ‎ ‎ 3‎