相似三角形的周长与面积2 4页

‎ ‎ 课 题27.2.3 相似三角形周长与面积 教 学 目 标 知识 技能 ‎1. 理解并掌握相似三角形及相似多边形的周长与面积的性质。‎ ‎2.能够运用相似三角形及相似多边形的周长与面积的性质解决相关问题。‎ 过程 方法 ‎1.通过操作、观察、猜想、类比、证明等数学活动，积累数学活动经验，感受 过程的条理性，进一步提高学生的数学思维能力和推理论证能力。‎ ‎2. 通过把多边形转化成三角形，体会转化思想在几何中的作用，同时让学生体会从特殊到一般的认识问题的方法。‎ 情感 态度 通过对性质的发现和论证的过程，感受数学活动充满着探索以及数学结论的确定性，提高学习热情、增强探究意识。‎ 重点 相似三角形和相似多边形的周长、面积的性质的理解与运用。‎ 难点 探索证明相似多边形面积的性质。‎ 教学方法 问题教学法、讨论法、练习法 板 书 设 计 4‎ ‎ ‎ 环节 教 学 问 题 设 计 情 境 引 入 旧知复习：‎ ‎1．如果两个三角形相似，那么它们的对应边、对应角各有什么特性？‎ ‎2．研究三角形问题，除了探讨边和角之外，我们还经常计算它的周长和面积，那么两个相似三角形的周长和面积有什么特征呢？‎ 教师提问，学生举手回答。（可画图，让学生结合图形回忆）‎ ‎ 教师点评、完善，为本节课的学习做好知识的链接。‎ ‎ 引出本课内容，板书课题。 ‎ 自 主 探 究 合 作 交 流 ‎【探究1】如果两个三角形相似，它们的周长之间什么关系？两个相似多边形呢？‎ ‎【问题】‎ 1． 请测量课前准备好的相似比为的两个相似三角形的各边长并分别计算周长，根据结果能猜想得出什么结论？‎ 2． 类比着猜想两个相似多边形的周长之间会有什么关系？‎ 3． 写出你得到的两个命题。‎ 4． 请根据命题1的题设和结论写出已知和求证。‎ 5． 请分析如何证明？写出证明过程。‎ 6． 类似的，如何证明命题2？‎ ‎【探究2】 如果两个三角形相似，它们的面积有什么关系？‎ ‎【问题】如图27.2.3—1，∆ABC∽∆A1B1C1，相似比为k1 ，它们的面积比是多少？‎ 图27.2.3—1‎ 1、 欲探讨三角形的面积，图中还需要添加什么辅助线？‎ 2、 相似三角形对应边上的高与相似比有何关系？怎么证明？‎ 3、 如何计算两相似三角形的面积比？‎ 4、 面积比与相似比关系如何？‎ 5、 总结所得结论并规范写出证明过程。‎ ‎6、相似三角形的对应中线的比、对应角平分线的比都等于相似比吗？‎ 教师请一位学生说出其测量结果集猜想的结论。‎ 教师点拨、纠偏，引导学生正确书写命题。‎ 学生回答后，老师板书命题1的已知、求证。‎ 鼓励并引导学生分析、讨论证法。写出规范的证明过程。‎ 学生独立完成命题2的证明。‎ 学生体会类比和转化方法的运用。‎ ‎ 复习三角形面积公式，教师启发学生作出三角形一组对应边上的高。‎ ‎ 教师引导学生测量并分析证明“相似三角形对应高的比等于相似比”。‎ 学生口述证明方法及过程，教师纠偏。‎ ‎ 启发学生先表示出两个三角形的面积再作比，从而通过观察结果与相似比进行对比后得出结论。‎ 学生独立思考完成，之后小组内交流。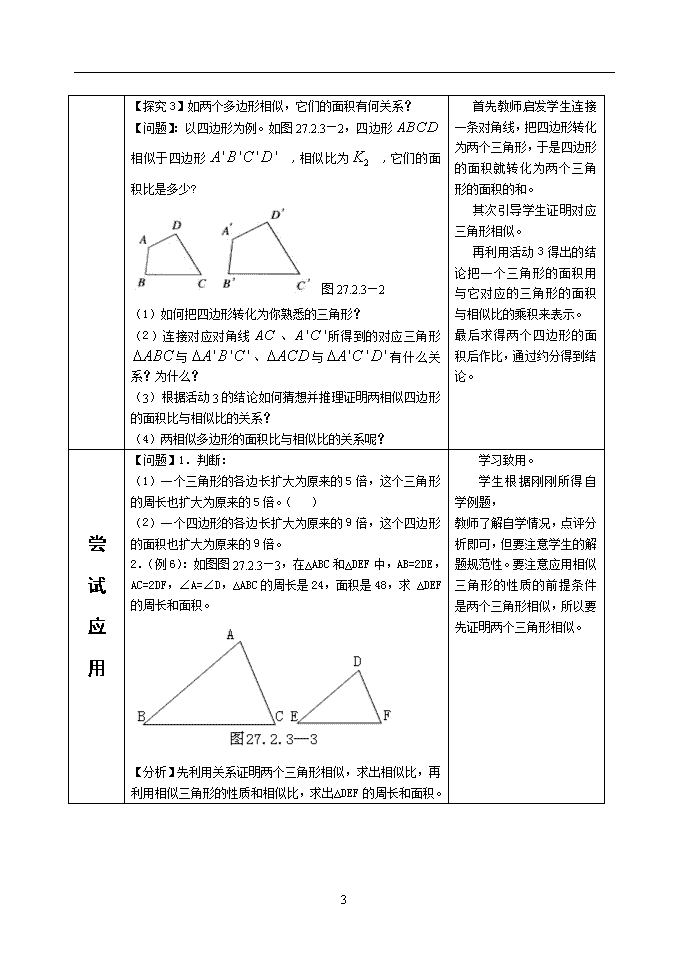‎ 4‎ ‎ ‎ ‎【探究3】如两个多边形相似，它们的面积有何关系？‎ ‎【问题】：以四边形为例。如图27.2.3—2，四边形相似于四边形　,相似比为　,它们的面积比是多少?‎ 图27.2.3—2‎ ‎（1）如何把四边形转化为你熟悉的三角形？‎ ‎（2）连接对应对角线、所得到的对应三角形与、与有什么关系？为什么？‎ ‎（3）根据活动3的结论如何猜想并推理证明两相似四边形的面积比与相似比的关系？‎ ‎（4）两相似多边形的面积比与相似比的关系呢？‎ 首先教师启发学生连接一条对角线，把四边形转化为两个三角形，于是四边形的面积就转化为两个三角形的面积的和。‎ 其次引导学生证明对应三角形相似。‎ 再利用活动3得出的结论把一个三角形的面积用与它对应的三角形的面积与相似比的乘积来表示。‎ 最后求得两个四边形的面积后作比，通过约分得到结论。‎ 尝 试 应 用 ‎【问题】1．判断：‎ ‎（1）一个三角形的各边长扩大为原来的5倍，这个三角形的周长也扩大为原来的5倍。（ ）‎ ‎（2）一个四边形的各边长扩大为原来的9倍，这个四边形的面积也扩大为原来的9倍。‎ ‎2．（例6）：如图图27.2.3—3，在∆ABC和∆DEF中，AB=2DE，AC=2DF，∠A=∠D，∆ABC的周长是24，面积是48，求 ∆DEF的周长和面积。‎ ‎【分析】先利用关系证明两个三角形相似，求出相似比，再利用相似三角形的性质和相似比，求出∆DEF的周长和面积。‎ 学习致用。‎ 学生根据刚刚所得自学例题，‎ 教师了解自学情况，点评分析即可，但要注意学生的解题规范性。要注意应用相似三角形的性质的前提条件是两个三角形相似，所以要先证明两个三角形相似。‎ 4‎ ‎ ‎ 成果 展示 1． 通过本节课的学习，谈谈自己的收获.‎ 2． 引导学生对上面的问题进行展示交流:‎ 相似三角形和相似多边形有哪些性质？‎ 研究多边形问题时通常会把它如何转化？‎ 学习小组内互相交流，讨论，展示.‎ 在活动中教师应重点关注：‎ 学生对于相似多边形的性质的运用的掌握情况．‎ 补 偿 提 高 ‎【问题】如图27.2.3—4，在△ABC和△DEF中，AB=DE，AC=DF，∠A=∠D，△ABC的周长是24，面积是，求△DEF的周长和面积。‎ 教师提出问题，学生思考，讨论.‎ 重点还是如何自用相似比求解 ‎ 教师分享学生的思路，并及时地点评.‎ 最后教师讲解.‎ 作 业 设 计 必做题 ‎1．课本习题27.2第6题、第13题 ‎2．预习27.2.3相似三角形的周长与面积，做《同步学习》自主学习 选做题：‎ ‎1．课本习题27.2第14题 ‎2.课本复习题第9题.‎ 教师布置作业，并提出要求.‎ 学生课下独立完成，延续课堂.‎ ‎ ‎ 教 后 反 思 ‎ ‎ 4‎