2019九年级数学上册 专题突破讲练 四点共圆问题大盘点试题 （新版）青岛版 14页

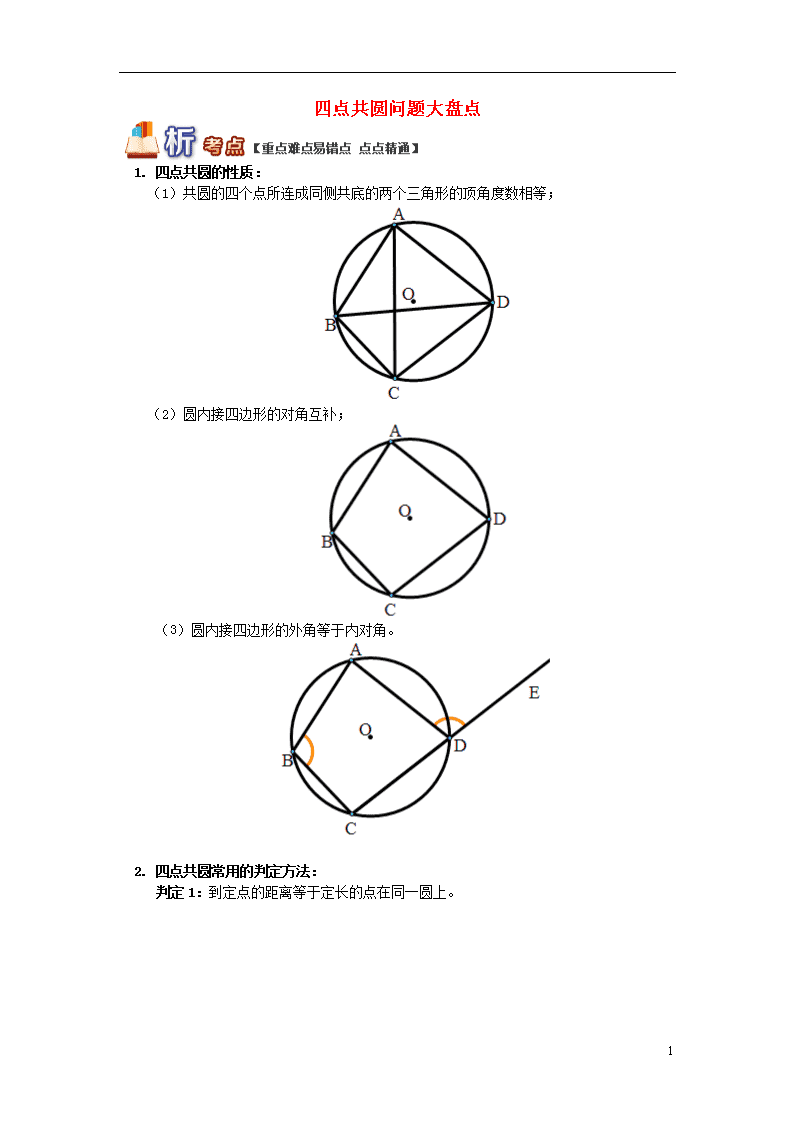
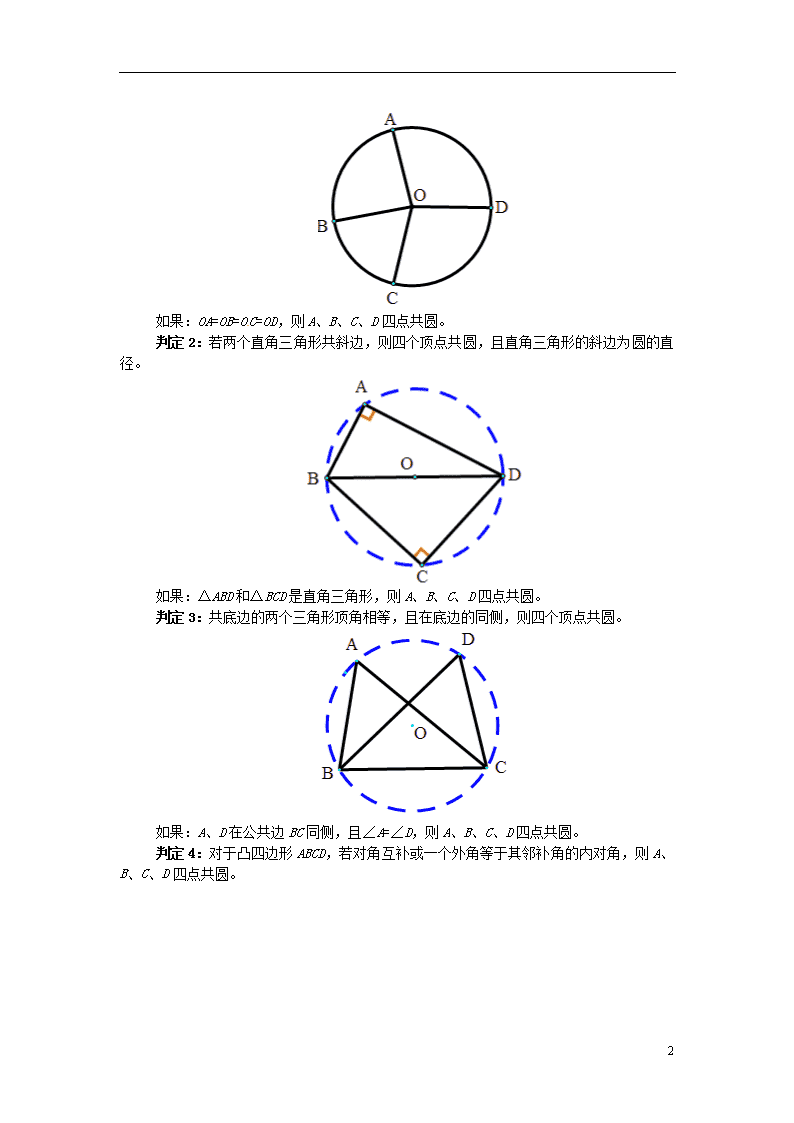
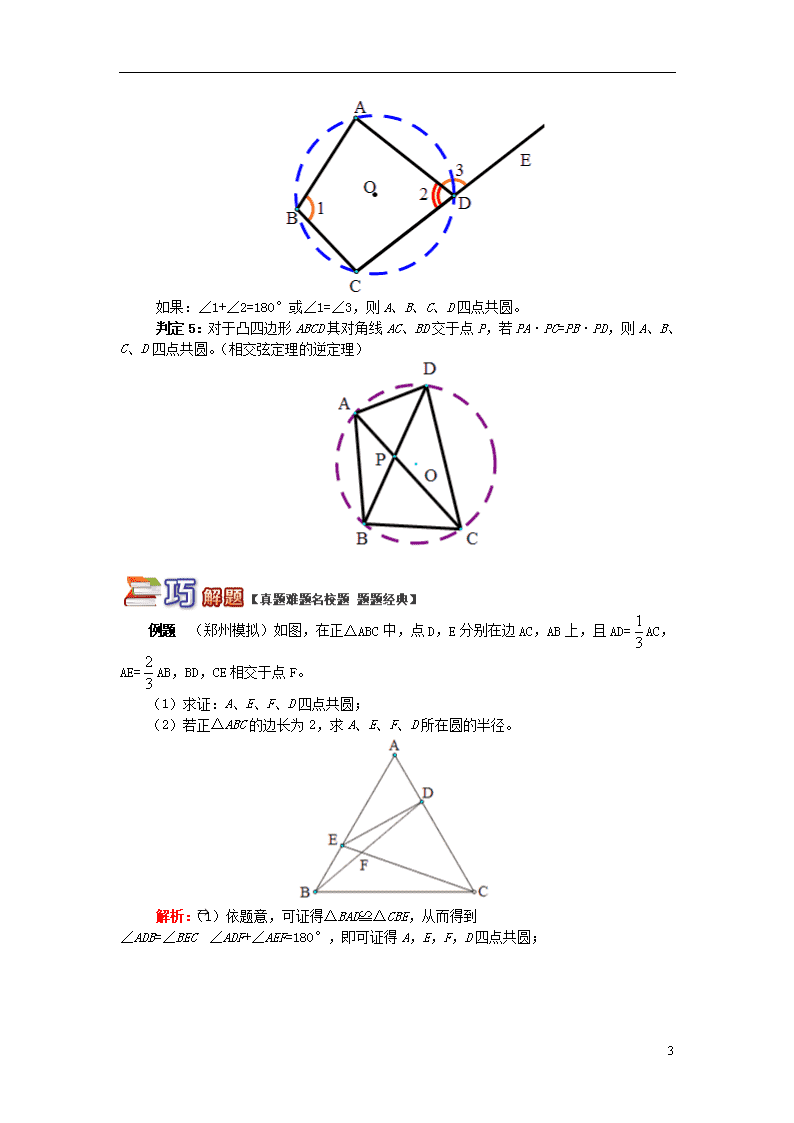
四点共圆问题大盘点 ‎1. 四点共圆的性质：‎ ‎（1）共圆的四个点所连成同侧共底的两个三角形的顶角度数相等；‎ ‎（2）圆内接四边形的对角互补；‎ ‎（3）圆内接四边形的外角等于内对角。‎ ‎2. 四点共圆常用的判定方法：‎ 判定1：到定点的距离等于定长的点在同一圆上。 ‎ 14‎ 如果：OA=OB=OC=OD，则A、B、C、D四点共圆。‎ 判定2：若两个直角三角形共斜边，则四个顶点共圆，且直角三角形的斜边为圆的直径。 ‎ 如果：△ABD和△BCD是直角三角形，则A、B、C、D四点共圆。‎ 判定3：共底边的两个三角形顶角相等，且在底边的同侧，则四个顶点共圆。 ‎ 如果：A、D在公共边BC同侧，且∠A=∠D，则A、B、C、D四点共圆。‎ 判定4：对于凸四边形ABCD，若对角互补或一个外角等于其邻补角的内对角，则A、B、C、D四点共圆。 ‎ 14‎ 如果：∠1+∠2=180°或∠1=∠3，则A、B、C、D四点共圆。‎ 判定5：对于凸四边形ABCD其对角线AC、BD交于点P，若PA·PC=PB·PD，则A、B、C、D四点共圆。（相交弦定理的逆定理）‎ 例题 （郑州模拟）如图，在正△ABC中，点D，E分别在边AC，AB上，且AD=AC，AE=AB，BD，CE相交于点F。‎ ‎（1）求证：A、E、F、D四点共圆；‎ ‎（2）若正△ABC的边长为2，求A、E、F、D所在圆的半径。‎ 解析：（1）依题意，可证得△BAD≌△CBE，从而得到∠ADB=∠BEC⇒∠ADF+∠AEF=180°，即可证得A，E，F，D四点共圆；‎ 14‎ ‎（2）取AE的中点G，连接GD，可证得△AGD为正三角形，GA=GE=GD=，即点G是△AED外接圆的圆心，且圆G的半径为。‎ 答案：（1）证明：∵AE=AB，‎ ‎∴BE=AB，‎ ‎∵在正△ABC中，AD=AC，‎ ‎∴AD=BE，‎ 又∵AB=BC，∠BAD=∠CBE，‎ ‎∴△BAD≌△CBE，‎ ‎∴∠ADB=∠BEC，‎ 即∠ADF+∠AEF=180°，所以A，E，F，D四点共圆。 ‎ ‎（2）解：如图，‎ 取AE的中点G，连接GD，则AG=GE=AE，‎ ‎∵AE=AB，‎ ‎∴AG=GE=AB=，‎ ‎∵AD=AC=，∠DAE=60°，AB=AC ‎∴△AGD为正三角形，‎ ‎∴GD=AG=AD=，即GA=GE=GD=，‎ 所以点G是△AED外接圆的圆心，且圆G的半径为，‎ 由于A，E，F，D四点共圆，即A，E，F，D四点共圆G，其半径为。‎ 点拨：本题着重考查全等三角形的证明与四点共圆的证明，突出推理能力与分析运算能力的考查，属于难题。‎ ‎【方法定位】‎ 14‎ 将已知条件、欲求的结论以及所给图形的特点三个方面认真分析、思考，即可发现，适当利用四点共圆的有关性质以及定理，就能巧妙地找到解决问题的途径。也就是说，四点共圆有时在解（证）题中起着“搭桥铺路”的作用。‎ 例题 （河南模拟）如图：AB是⊙O的直径，G是AB延长线上的一点，GCD是⊙O的割线，过点G作AG的垂线，交直线AC于点E，交直线AD于点F，过点G作⊙O的切线，切点为H。‎ ‎（1）求证：C，D，E，F四点共圆；‎ ‎（2）若GH=6，GE=4，求EF的长。‎ 解析：（1）连接DB，利用AB是⊙O的直径，可得∠ADB=90°，在Rt△ABD和Rt△AFG中，∠ABD=∠AFE，又同弧所对的圆周角相等可得∠ACD=∠ABD，进而得到∠ACD=∠AFE即可证明四点共圆；‎ ‎（2）由C，D，E，F四点共圆，利用共线定理可得GE·GF=GC·GD。由GH是⊙O的切线，利用切割线定理可得GH2=GC·GD，进而得到GH2=GE·GF。即可 答案：‎ 证明：（1）连接DB，∵AB是⊙O的直径，∴∠ADB=90°，‎ 在Rt△ABD和Rt△AFG中，∠ABD=∠AFE，‎ 又∵∠ABD=∠ACD，∴∠ACD=∠AFE。‎ ‎∴C，D，E，F四点共圆；‎ ‎（2）∵C，D，E，F四点共圆，∴GE·GF=GC·GD。‎ ‎∵GH是⊙O的切线，∴GH2=GC·GD，∴GH2=GE·GF。‎ 又因为GH=6，GE=4，所以GF=9。‎ ‎∴EF=GF－GE=9－4=5。‎ 点拨：熟练掌握圆的切线的性质、同弧所对的圆周角相等、四点共圆的判定方法、切割线定理等是解题的关键。此题综合性较强，涉及知识点较全面。‎ ‎（答题时间：30分钟）‎ 一、选择题 ‎ ‎1. 锐角△ABC的三条高AD、BE、CF交于H，在A、B、C、D、E、F、H七个点中。能组成四点共圆的组数是（　　）‎ ‎ A. 4组 B. 5组 C. 6组 D. 7组 14‎ ‎2. 如图，在四边形ABCD中，AC、BD为对角线，点M、E、N、F分别为AD、AB、BC、CD边的中点，下列说法：‎ ‎①当AC=BD时，M、E、N、F四点共圆。‎ ‎②当AC⊥BD时，M、E、N、F四点共圆。‎ ‎③当AC=BD且AC⊥BD时，M、E、N、F四点共圆。‎ 其中正确的是（　　）‎ A. ①② B. ①③ C. ②③ D. ①②③‎ ‎3. 如图，A，B，C，D是圆上四点，AD，BC的延长线交于点P，弧AB、弧CD分别为100°、40°，则∠P的度数为（　　）‎ A. 40° B. 35° C. 60° D. 30°‎ ‎4. （高青县模拟）如图，四边形ABCD内接于⊙O，AB为⊙O的直径，CM切⊙O于点C，∠BCM=60°，则∠B的正切值是（　　）‎ ‎ A. B. C. D. ‎ ‎5. 已知Pi（i=1，2，3，4）是抛物线y=x2+bx+1上共圆的四点，它们的横坐标分别为xi（i=1，2，3，4），又xi（i=1，2，3，4）是方程（x2－4x+m）（x2－4x+n）=0的根，则二次函数y=x2+bx+1的最小值为（　　）‎ A. －1 B. －‎2 ‎C. －3 D. －4‎ 二、填空题 ‎6. 如图，在△ABC中，AD，BE分别是∠A，∠B的角平分线，O是AD与BE的交点，若C，D，O，E四点共圆，DE=3，则△ODE的内切圆半径为 。‎ 14‎ ‎7. （济宁）如图，四边形ABCD中，AB=AC=AD，若∠CAD=76°，则∠CBD=　　度。‎ ‎8. 已知△ABC的中线AD、BE交于K，AB=，且K，D，C，E四点共圆，则CK= 。‎ ‎**9. 如图，CD为△ABC外接圆的切线，AB的延长线交直线CD于点D，E，F分别为弦AB与弦AC上的点，且BC·AE=DC·AF，B，E，F，C四点共圆。若DB=BE=EA，则过B，E，F，C四点的圆的面积与△ABC外接圆面积的比值为 。‎ 三、解答题 ‎10. （太原模拟）如图，已知AB为半圆O的直径，BE、CD分别为半圆的切线，切点分别为B、C，DC的延长线交BE于F，AC的延长线交BE于E。AD⊥DC，D为垂足。‎ ‎（1）求证：A、D、F、B四点共圆；‎ ‎（2）求证：EF=FB。‎ 14‎ ‎*11. （贵阳模拟）如图，AP是圆O的切线，A是切点，AD⊥OP于D点，过点P作圆O的割线与圆O相交于B，C两点。‎ ‎（1）证明：O、D、B、C四点共圆。‎ ‎（2）设∠OPC=30°，∠ODC=40°，求∠DBC的大小。‎ ‎*12. （长春模拟）如图，在△ABC中，∠C为钝角，点E，H分别是边AB上的点，点K和M分别是边AC和BC上的点，且AH=AC，EB=BC，AE=AK，BH=BM。‎ ‎（1）求证：E、H、M、K四点共圆；‎ ‎（2）若KE=EH，CE=3，求线段KM的长。‎ 14‎ 一、选择题 ‎1. C ‎ 解析：如图，以AH为斜边的两个直角三角形，四个顶点共圆（A、F、H、E），‎ 以BH为斜边的两个直角三角形，四个顶点共圆（B、F、H、D），‎ 以CH为斜边的两个直角三角形，四个顶点共圆（C、D、H、E），‎ 以AB为斜边的两个直角三角形，四个顶点共圆（A、E、D、B），‎ 以BC为斜边的两个直角三角形，四个顶点共圆（B、F、E、C），‎ 以AC为斜边的两个直角三角形，四个顶点共圆（A、F、D、C），‎ 共6组。‎ 故选C。‎ ‎2. C ‎ 解析：连接EM、MF、FN、NE，连接EF、MN，交于点O，如图所示，‎ ‎∵点M、E、N、F分别为AD、AB、BC、CD边的中点，‎ ‎∴EM∥BD∥NF，EN∥AC∥MF，EM=NF=BD，EN=MF=AC，‎ ‎∴四边形ENFM是平行四边形，‎ ‎①当AC=BD时，‎ 则有EM=EN，‎ 所以平行四边形ENFM是菱形，‎ 而菱形的四个顶点不一定共圆，‎ 故①不一定正确；‎ ‎②当AC⊥BD时，‎ 由EM∥BD，EN∥AC可得：EM⊥EN，即∠MEN=90°，‎ 所以平行四边形ENFM是矩形，‎ 则有OE=ON=OF=OM。‎ 所以M、E、N、F四点共圆，‎ 故②正确；‎ ‎③当AC=BD且AC⊥BD时，‎ 同理可得：四边形ENFM是正方形。‎ 则有OE=ON=OF=OM。‎ 所以M、E、N、F四点共圆，‎ 故③正确。‎ 故选C。‎ 14‎ ‎3. D 解：连接BD，‎ ‎∵=100°，‎ ‎∴∠ADB=100°×=50°，‎ 又∵=40°，‎ ‎∴∠B=20°，‎ 在△DBP中，∠P=∠ADB－∠B=50°－20°=30°。‎ 故选D。‎ ‎4. B 解：连接BD，‎ AB是直径，则∠ADB=90°，‎ ‎∴∠CDB=∠BCM=60°，‎ ‎∴∠CDA=∠CDB+∠ADB=150°，‎ ‎∵∠CBA=180°－∠CDA=30°，‎ ‎∴tan∠ABC=tan30°=，‎ 故选B。‎ ‎5. C 解：抛物线与圆的四个交点，上下两组点的连线的中点位于抛物线的对称轴上。‎ 所以由（x2－4x+m）（x2－4x+n）=0可知，该抛物线的对称轴为x=2。‎ 则b=－4。‎ 所以最小值为。‎ 14‎ 二、填空题 ‎6. 解：作OF⊥ED于点F，‎ ‎∵AD，BE分别是∠A，∠B的角平分线，‎ ‎∴∠AOB=90°+∠C，CO平分∠ACB，‎ 又∵∠DOE=∠AOB，∠DOE+∠C=180°，‎ ‎∴∠C=60°，∠DOE=∠AOB=120°，‎ ‎∴90°+∠C＋∠C=180°‎ 在AB上截取AM=AE，可得△AOE△AOM ‎∴OE=OM，‎ ‎∵∠DOE=120°，‎ ‎∴∠EOA=∠AOM=∠DOB=∠BOM =60°，‎ ‎∴△BOM△BOD ‎∴OD=OM，‎ ‎∴OD=OE，‎ ‎∴∠OED=∠ODE=30°，‎ ‎∴FD=，‎ tan30°=，‎ ‎∴FO=，OD=OE=，‎ ‎∴△ODE的周长为：2+3，‎ ‎∴△ODE的面积为：×3×=，‎ ‎∴△ODE的内切圆半径为，‎ 故答案为：。‎ ‎7. 解：∵AB=AC=AD，‎ ‎∴点B，C，D可以看成是以点A为圆心，AB为半径的圆上的三个点，‎ 14‎ ‎∴∠CBD是弧CD所对的圆周角，∠CAD是弧CD所对的圆心角；‎ ‎∵∠CAD=76°，‎ ‎∴∠CBD=∠CAD=×76°=38°。‎ ‎8. 解：作△ABC的外接圆，延长CK交圆于点H，交AB于F，则∵K，D，C，E四点共圆，DE∥BA ‎∴∠BHC=∠BAC=∠DEC=∠DKC，‎ ‎∴AK∥HB，‎ ‎∵D为BC的中点 ‎∴点K是CH的中点，即CK=KH，‎ 又K是重心，‎ ‎∴FK=HF=CF，‎ 由相交弦定理，得BF×FA=CF×FH，‎ ‎∴·=CF2，‎ ‎∴CF=，‎ ‎∴CK==1，‎ 故答案为1。‎ ‎9. 解：如图所示，‎ 连接EF。∵DC是△ABC的外接圆的切线，∴∠DCB=∠EAF，‎ ‎∵BC·AE=DC·AF，∴，‎ ‎∴△BCD≌△FAE，‎ ‎∴∠CBD=∠AFE，‎ ‎∵B、E、F、C四点共圆，‎ ‎∴∠AFE=∠CBE，‎ ‎∴∠CBD=∠CBE，‎ 又∵∠CBD+∠CBE=180°，∴∠CBE=90°，‎ ‎∴AC是△ABC的外接圆的直径，CE是E，F，C四点所在圆的直径。‎ 不妨设DB=1，则BE=EA=DB=1，‎ 由切割线定理可得：DC2=DB•DA=1×3，，‎ 14‎ 在△DCE中，由DB=BE，CB⊥DE。∴CE=DC=，‎ 在Rt△CBE中，BC2=CE2－BE2=，‎ 在Rt△ABC中，AC2=BC2+AB2=2+22=6。‎ ‎∴过B，E，F，C四点的圆的面积与△ABC外接圆面积的比值=。‎ 故答案为。‎ 三、解答题 ‎10. 证明：（1）∵FB是半圆O的切线，‎ ‎∴∠ABF=90°，‎ 又∵AD⊥DC，‎ ‎∴∠ADF=90°，‎ ‎∴A，D，F，B四点共圆。‎ ‎（2）解：连接BC，则BC⊥AC，‎ ‎∵DF是半圆的切线，‎ ‎∴∠DCA=∠ABC，‎ ‎∵∠DCA=∠ECF，‎ ‎∴∠ECF=∠ABC，‎ 在Rt△ABE中，BC⊥AE，‎ ‎∴∠ABC=∠E，‎ ‎∴∠ECF=∠E，∴EF=FC，‎ ‎∵FC，FB是半圆的切线，‎ ‎∴FC=FB，‎ ‎∴EF=FB。‎ ‎11. 解：（1）证明：∵AP是圆O的切线，A是切点，‎ ‎∴OA⊥AP，‎ ‎∵AD⊥OP，‎ 14‎ ‎∴AP2=PD·PO，‎ ‎∵AP是圆O的切线，PBC是圆O的割线，‎ ‎∴AP2=PB·PC，‎ ‎∴PD·PO=PB·PC，‎ ‎∴，‎ ‎∵∠DPB=∠CPO，‎ ‎∴△DPB∽△CPO，‎ ‎∴∠PDB=∠PCO，‎ ‎∴O，D，B，C四点共圆；‎ ‎（2）解：连接OB，则∠OBC=∠ODC=40°，‎ ‎∴∠OCB=40°，‎ ‎∵O，D，B，C四点共圆，‎ ‎∴∠PDB=∠OCB=40°，‎ ‎∴∠DBC=30°+40°=70°。‎ ‎12. （1）证明：连接CH，∵AC=AH，AK=AE，∴四边形CHEK为等腰梯形，‎ 注意到等腰梯形的对角互补，‎ 故C，H，E，K四点共圆， ‎ 同理C，E，H，M四点共圆，‎ 即E，H，M，K均在点C，E，H所确定的圆上。 ‎ ‎（2）解：连接EM，‎ 由（1）得E，H，M，C，K五点共圆，‎ ‎∵CEHM为等腰梯形，∴EM=HC，‎ 故∠MKE=∠CEH，‎ 由KE=EH可得∠KME=∠ECH，‎ 故△MKE≌△CEH，‎ 即KM=EC=3。 ‎ 14‎