中考数学一轮精品学案：创新实践与操作问题 2页

‎ ‎ 创新实践与操作 ‎ ‎ ‎【学习目标】 ‎ ‎1． 通过学生动手操作解决实际问题；‎ ‎2． 培养学生动手实践能力和创新能力．‎ ‎【巩固练习】‎ 一、选择题：‎ ‎1．（10温州）用若干根相同的火柴棒首尾顺次相接围成一个梯形（提供的火柴棒全部用完），下列根数的火柴棒不能围成梯形的是 （ ）‎ A．5 B．6 C．7 D．8‎ ‎2．（10宁德）如图所示，如果将矩形纸沿虚线①对折后，沿虚线②剪开，剪出一个 直角三角形，展开后得到一个等腰三角形.则展开后三角形的周长是 （ ）‎ A．2＋ B．2＋2 C．12 D．18 ‎ ‎3. (10安徽)在二行三列的方格棋盘上沿骰子的某条棱翻动骰子（相对面上分别标有1点和6点，2点和5点，3点和4点），在每一种翻动方式中，骰子不能后退．开始时骰子如图（1）那样摆放，朝上的点数是2；最后翻动到如图（2）所示的位置，此时骰子朝上的点数不可能是下列数中的 （ ）‎ ‎（第5题图）‎ ‎（第4题图）‎ A．5 B．4 C．3 D．1‎ ‎4.（10晋江）如图，将一张正方形纸片剪成四个小正方形，得到4个小正方形，称为第一次操作；然后，将其中的一个正方形再剪成四个小正方形，共得到7个小正方形，称为第二次操作；再将其中的一个正方形再剪成四个小正方形，共得到10个小正方形，称为第三次操作；...，根据以上操作，若要得到2011个小正方形，则需要操作的次数是( ) .‎ A. 669 B. 670　 C.671 D. 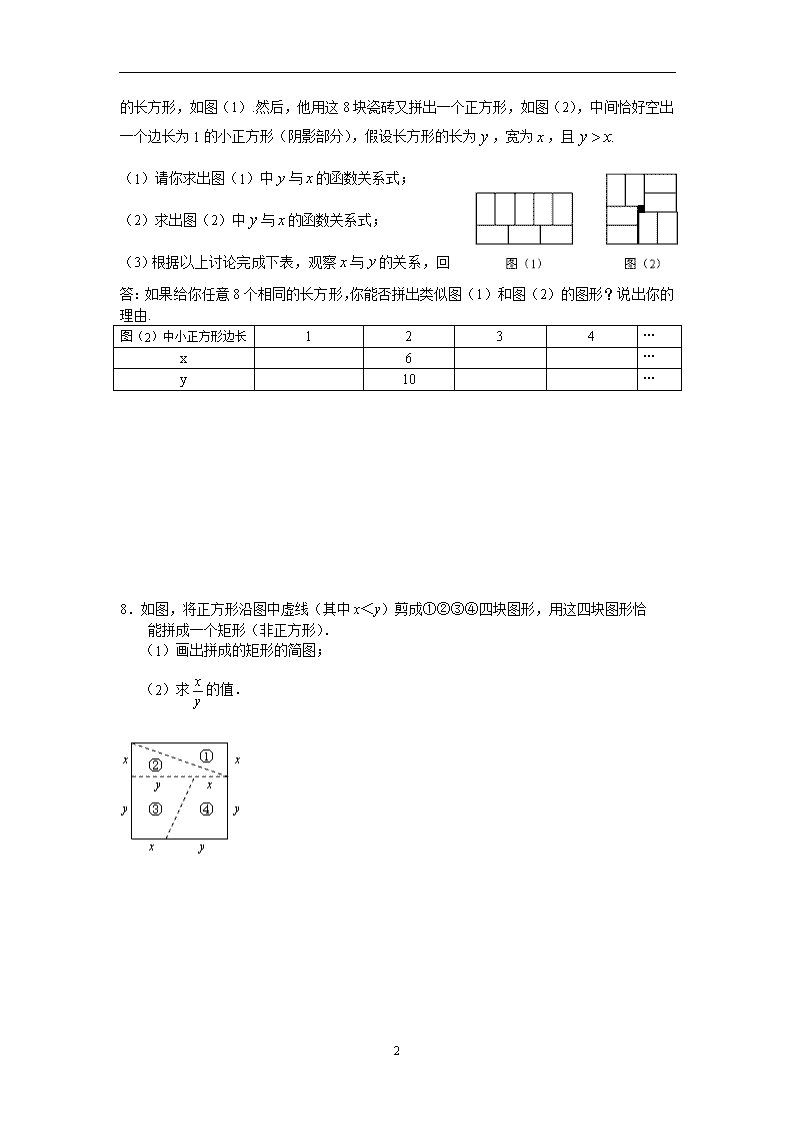672‎ 二、填空题：‎ ‎5．(09内江)如图，小陈从O点出发，前进5米后向右转20O，再前进5米后又向右转20O，……，这样一直走下去，他第一次回到出发点O时一共走了 米.‎ ‎6．（09绍兴）李老师从油条的制作受到启发，设计了一个数学问题：如图，在数轴上截取从原点到1的对应点的线段，对折后（点与重合）再均匀地拉成1个单位长度的线段，这一过程称为一次操作（如在第一次操作后，原线段上的，均变成，变成1，等）．那么在线段上（除，）的点中，在第二次操作后，恰好被拉到与1重合的点所对应的数之和是____________．‎ ‎（第6题图）‎ 三、解答题：‎ ‎7．（10新疆）张师傅在铺地板时发现，用8块大小 2‎ ‎ ‎ 一样的长方形瓷砖恰好可以拼成一个大的长方形，如图（1）.然后，他用这8块瓷砖又拼出一个正方形，如图（2），中间恰好空出一个边长为1的小正方形（阴影部分），假设长方形的长为，宽为，且 ‎（1）请你求出图（1）中与的函数关系式；‎ ‎（2）求出图（2）中与的函数关系式；‎ ‎（3）根据以上讨论完成下表，观察与的关系，回答：如果给你任意8个相同的长方形，你能否拼出类似图（1）和图（2）的图形？说出你的理由.‎ 图（2）中小正方形边长 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎…‎ x ‎6‎ ‎…‎ y ‎10‎ ‎…‎ ‎8．如图，将正方形沿图中虚线（其中x＜y）剪成①②③④四块图形，用这四块图形恰 能拼成一个矩形（非正方形）．‎ ‎（1）画出拼成的矩形的简图；‎ ‎（2）求的值．‎ 2‎