2012年初三数学丰台一模试题 6页

北京市丰台区 2011-2012 学年度第二学期初三综合练习（一） 数 学 试 卷 学校 　　　 姓名 一、选择题（本题共 32 分，每小题 4 分） 1． 的相反数是 A． B． C． D． 2．据统计，今年北京市中考报名确认考生人数是 96 200 人，用科学记数法表示 96 200 为 A． B． C． D． 3．下列图形中，是正方体的平面展开图的是 A． B． C． D． 4．在一个不透明的口袋中，装有 个红球和 个白球，它们除颜色外完全相同，从口袋 中任意摸出一个球，摸到红球的概率是 A． B． C． D． 5．如图，AB 是⊙O 的弦，OC 是⊙O 的半径，OC⊥AB 于点 D，若 AB= ， OD=3，则⊙O 的半径等于 A． B． C． D． 6．2012 年 4 月 21 日 8 时北京市部分区县的可吸入颗粒物数值统计如下表： 区 县 东城 西城 海淀 朝阳 丰台 大兴 延庆 昌平 可吸入颗粒物（mg/m3） 0.15 0.15 0.15 0.15 0.18 0.18 0.03 0.14 则这 8 个区县该日这一时刻的可吸入颗粒物数值的众数和中位数分别是 A．0.15 和 0.14 B．0.18 和 0.15 C．0.15 和 0.15 D． 0.18 和 0.14 7．若抛物线 的最低点的纵坐标为 n，则 m-n 的值是 A． B． C．1 D．2 3 3± 3 -3 1 3 49.62 10× 50.962 10× 59.62 10× 396.2 10× 4 3 4 7 3 7 3 1 1 4 8 4 5 8 10 2 2y x x m= − + -1 0 FE A C D B 8．如图，矩形 ABCD 中，AB=3，BC=5，点 P 是 BC 边上的一个动点 （点 P 不与点 B、C 重合），现将△PCD 沿直线 PD 折叠，使点 C 落到点 C’处；作∠BPC’的角平分线交 AB 于点 E．设 BP=x，BE=y， 则下列图象中，能表示 y 与 x 的函数关系的图象大致是 A． B． C ． D ． 二、填空题（本题共 16 分，每小题 4 分） 9． 如果若分式 的值为 0，那么 的值等于 ． 10． 如果一个正多边形的一个外角是 60°，那么这个正多边形的边数是 ． 11． 分解因式： ． 12．在数学校本活动课上，张老师设计了一个游戏，让电动娃娃在边长为 1 的正方形 的四个顶点上依次跳动．规定：从顶点 A 出发，每跳动一步的长均为 1．第一次顺 时针方向跳 1 步到达顶点 D，第二次逆时针方向跳 2 步到达顶点 B，第三次顺时针 方向跳 3 步到达顶点 C，第四次逆时针方向跳 4 步到达顶点 C，… ，以此类推， 跳动第 10 次到达的顶点是 ，跳动第 2012 次到达的顶点是 ． 三、解答题（本题共 30 分，每小题 5 分） 13．计算： ． 14．解不等式组： 15．已知 ，求代数式 的值． 16．已知：如图，AB∥CD，AB=CD，点 E、F 在线段 AD 上，且 AF=DE．求证：BE=CF． 1x x + x 3 9a a− = -1 02 2cos30 (π 3.14) 12+ + − − 4 8 0, 5 2 1 1. 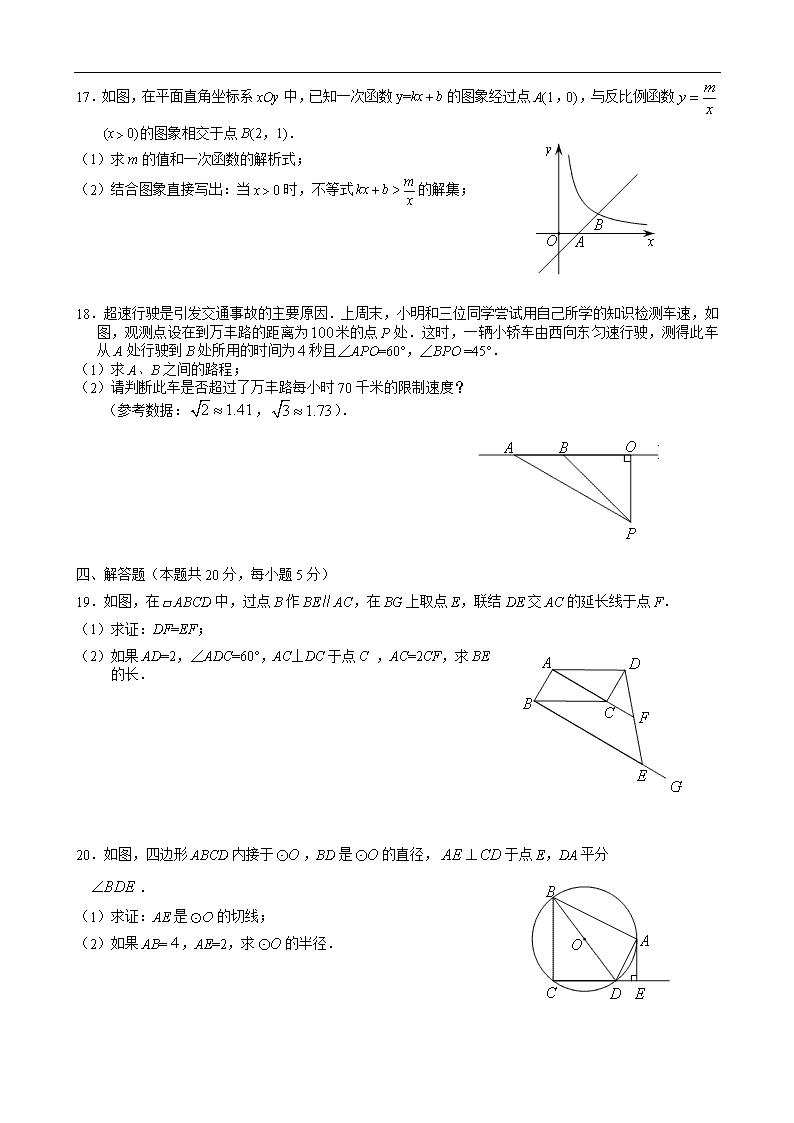x x + >  − − > （ ） 2 3 1 0x x+ − = 21 4 4 1 2 1 2 x x x x x x − + −⋅ −− + + A D CB E P C’ A D B C O 5 y xO 5 y xO x y 5O 5 y x 17．如图，在平面直角坐标系 xOy 中，已知一次函数 的图象经过点 A(1，0)，与反比例函数 (x 0)的图象相交于点 B(2，1)． （1）求 m 的值和一次函数的解析式； （2）结合图象直接写出：当 x 0 时，不等式 的解集； 18．超速行驶是引发交通事故的主要原因．上周末，小明和三位同学尝试用自己所学的知识检测车速，如 图，观测点设在到万丰路的距离为 米的点 P 处．这时，一辆小轿车由西向东匀速行驶，测得此车 从 A 处行驶到 B 处所用的时间为 秒且∠APO=60°，∠BPO =45°． （1）求 A、B 之间的路程； （2）请判断此车是否超过了万丰路每小时 70 千米的限制速度？ （参考数据： ， ）． 四、解答题（本题共 20 分，每小题 5 分） 19．如图，在 ABCD 中，过点 B 作 BE∥AC，在 BG 上取点 E，联结 DE 交 AC 的延长线于点 F． （1）求证：DF=EF； （2）如果 AD=2，∠ADC=60°，AC⊥DC 于点 C ，AC=2CF，求 BE 的长． 20．如图，四边形 ABCD 内接于 ，BD 是 的直径， 于点 E，DA 平分 ． （1）求证：AE 是 的切线； （2）如果 AB= ，AE=2，求 的半径． y=kx b+ my x = > > mkx b x + > 100 4 2 1.41≈ 3 1.73≈  O O AE CD⊥ BDE∠ O 4 O O A C E B D x y B AO O P BA 万丰路 F D CB A E G CB A D 21．某学校为了解九年级学生的体育达标情况，从九年级学生中随机抽取若干名学生进行体 育测试，根据收集的数据绘制成如下统计图（图 1、图 2），请根据图中的信息解答下列问题： （1）补全图 1 与图 2； （2）若该学校九年级共有 400 名学生，根据统计结果可以估计九年级体育达标优秀和良好的学生共有 ___________名． 九年级学生体育测试成绩条形统计图 九年级学生体育测试成绩扇形统计图 22．将矩形纸片分别沿两条不同的直线剪两刀，可以使剪得的三块纸片恰能拼成一个等腰三 角形（不能有重叠和缝隙）． 小明的做法是：如图 1 所示，在矩形 ABCD 中，分别取 AD、AB、CD 的中点 P、E、 F，并沿直线 PE 、PF 剪两刀，所得的三部分可拼成等腰三角形△PMN (如图 2)． （1）在图 3 中画出另一种剪拼成等腰三角形的示意图； （2）以矩形 ABCD 的顶点 B 为原点，BC 所在直线为 x 轴建立平面直角坐标系（如图 4）， 矩形 ABCD 剪拼后得到等腰三角形△PMN，点 P 在边 AD 上（不与点 A、D 重合），点 M、N 在 x 轴 上（点 M 在 N 的左边）．如果点 D 的坐标为(5,8)，直线 PM 的解析式为 ，则所有满足条件 的 k 的值为 ． 图 1 图 2 图 3 图 4 备用 =y kx b+ x y DA B C x y DA B C 20% P E F DA B C 人数 成绩 0 4 812 16 20 24 2832 36 40 不及格 及格 良好 优秀 不及格 及格 良好 优秀 % 5% % 20% P E F DA B C 五、解答题（本题共 22 分，第 23 题 7 分，第 24 题 7 分，第 25 题 8 分） 23．已知：关于 x 的一元二次方程： . （1）求证：这个方程有两个不相等的实数根； （2）当抛物线 与 x 轴的交点位于原点的两侧，且到原点的距离相等时， 求此抛物线的解析式； （3）将（2）中的抛物线在 x 轴下方的部分沿 x 轴翻折，其余部分保持能够不变，得到图形 C1,将图形 C1 向右平移一个单位,得到图形 C2，当直线 (b<0)与图形 C2 恰有两个公共点时，写出 b 的取值范 围. 24．已知：△ABC 和△ADE 是两个不全等的等腰直角三角形，其中 BA=BC，DA=DE，联结 EC，取 EC 的 中点 M，联结 BM 和 DM． （1）如图 1，如果点 D、E 分别在边 AC、AB 上，那么 BM、DM 的数量关系与位置关系是 ； （2）将图 1 中的△ADE 绕点 A 旋转到图 2 的位置时，判断（1）中的结论是否仍然成立，并说明理由． 25．已知：如图，在平面直角坐标系 xOy 中，以点 P（2， ）为圆心的圆与 y 轴相切于 2 22 4 0x mx m− + − = 2 22 4y x mx m= − + − y=x b+ 3 D C B A E M M E A B C D 点 A，与 x 轴相交于 B、C 两点（点 B 在点 C 的左边）． （1）求经过 A、B、C 三点的抛物线的解析式； （2）在（1）中的抛物线上是否存在点 M，使△MBP 的面积是菱形 ABCP 面积的 ．如果 存在，请直接写出所有满足条件的 M 点的坐标；如果若不存在，请说明理由； （3）如果一个动点 D 自点 P 出发，先到达 y 轴上的某点，再 到达 x 轴上某点，最后运动到（1）中抛物线的顶点 Q 处，求使点 D 运动的总路径最短的路径的长．. 2 1