2020八年级数学下学期期末考前练习题综合题基础 6页

综合题（基础）‎ ‎1. 【解答题】计算：．‎ 答案：‎ 解：原式=++2-1‎ ‎=+2+1‎ ‎=3+1．‎ 解析利用零指数幂、负整数幂的意义和二次根式的乘法法则运算．‎ ‎2. 【解答题】计算：‎ ‎1小题1.× ．‎ 答案：‎ 解：×==9．‎ ‎2小题2.+   ．‎ 答案：‎ 解：+=3+4=7．‎ 6‎ ‎3小题3.+．‎ 答案：‎ 解：+=3-4=-1．‎ 解析(1)根据两个二次根式相乘，把被开方数相乘，再化简可得结果；‎ ‎(2)先把二次根式化为最简二次根式，再合并；‎ ‎(3)根据算术平方根和立方根的定义可得结果．‎ ‎3. 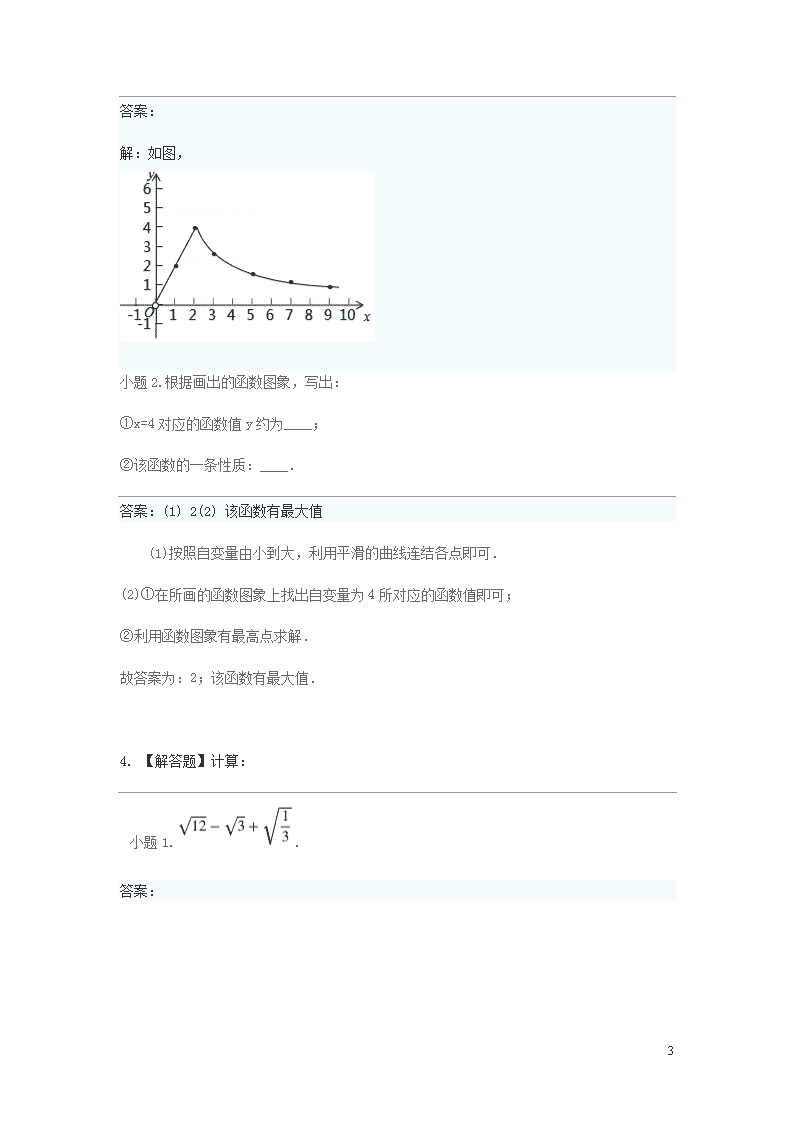【解答题】已知y是x的函数，自变量x的取值范围x>0，下表是y与x的几组对应值：‎ x ‎…‎ ‎1‎ ‎2‎ ‎3‎ ‎5‎ ‎7‎ ‎9‎ ‎…‎ y ‎…‎ ‎1.98‎ ‎3.95‎ ‎2.63‎ ‎1.58‎ ‎1.13‎ ‎0.88‎ ‎…‎ 小腾根据学习函数的经验，利用上述表格所反映出的y与x之间的变化规律，对该函数的图象与性质进行了探究．‎ 下面是小腾的探究过程，请补充完整：‎ 小题1.如图，在平面直角坐标系xOy中，描出了以上表格中各对对应值为坐标的点，根据描出的点，画出该函数的图象． ‎ 6‎ 答案：‎ 解：如图， ‎ 小题2.根据画出的函数图象，写出：‎ ‎①x=4对应的函数值y约为____；‎ ‎②该函数的一条性质：____．‎ 答案：(1) 2(2) 该函数有最大值 解析(1)按照自变量由小到大，利用平滑的曲线连结各点即可．‎ ‎(2)①在所画的函数图象上找出自变量为4所对应的函数值即可；‎ ‎②利用函数图象有最高点求解．‎ 故答案为：2；该函数有最大值．‎ ‎4. 【解答题】计算：‎ ‎1小题1.．‎ 答案：‎ 6‎ 解：原式= =．‎ ‎2小题2.．‎ 答案：‎ 解：原式=÷3 =÷3 =．‎ 解析(1)先把二次根式化为最简二次根式，然后合并即可； (2)先把二次根式化为最简二次根式，然后合并后进行二次根式的除法运算．‎ ‎5. 【解答题】已知x=+1，求x2-2x的值．‎ 答案：‎ 解：原式=x(x-2)，‎ 当x=+1时，‎ 原式=(+1)(-1)‎ ‎=5-1‎ 6‎ ‎=4．‎ 解析先因式分解x2-2x=x(x-2)，再根据二次根式的性质即可求出答案．‎ ‎6. 【解答题】解不等式：．‎ 答案：‎ 解：移项合并得：()x<3， 解得：x>，即x>-3-3．‎ 解析不等式移项合并，把x系数化为1，即可求出解集．‎ ‎7. 【解答题】如图，在平面直角坐标系xOy中，直线y=-2x+4与x轴，y轴分别交于点A，点B． ‎ ‎1小题1.求点A和点B的坐标．‎ 答案：‎ 解：令x=0，得y=4；令y=0，得x=2； ∴B(0，4)，A(2，0)．‎ ‎2小题2.若点P在y轴上，且S△AOP=S△AOB，求点P的坐标．‎ 6‎ 答案：‎ 解：设P(0，m)， ∵S△AOP=S△AOB， ∴×|m|×2=××2×4， ∴m=±2， ∴P(0，2)或(0，-2)．‎ 解析(1)将x=0，y=0分别代入一次函数，即可求出坐标； (2)设P(0，m)，构建方程即可解决问题．‎ 6‎