江苏省江阴市第二中学2012-2013学年高一上学期期中考试数学试题 7页

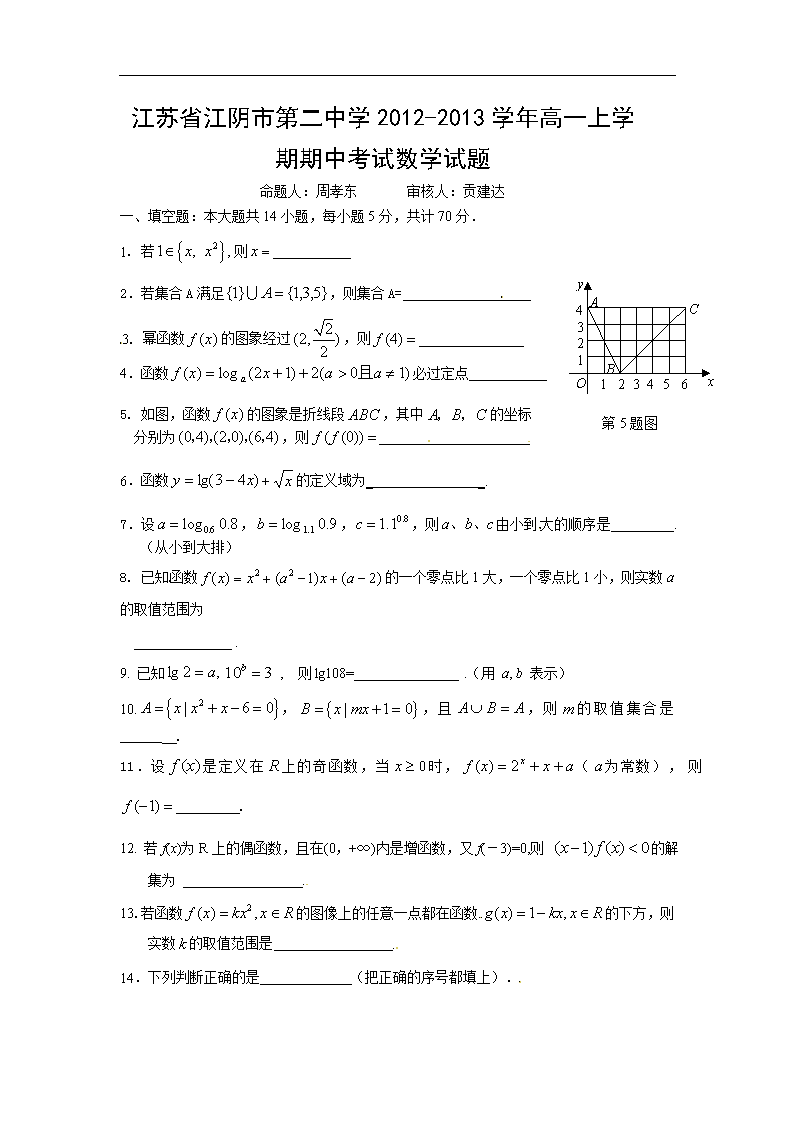
江苏省江阴市第二中学2012-2013学年高一上学期期中考试数学试题 命题人：周孝东 审核人：贡建达 一、填空题：本大题共14小题，每小题5分，共计70分．‎ ‎2‎ B C A y x ‎1‎ O ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎1. 若则 ‎ ‎2．若集合A满足，则集合A= ‎ ‎3. 幂函数的图象经过，则_______________‎ 第5题图 ‎4．函数必过定点 ‎ ‎5. 如图，函数的图象是折线段，其中的坐标 分别为，则 ‎ ‎6．函数+的定义域为_ _.‎ ‎7．设，，，则由小到大的顺序是_ _.（从小到大排）‎ ‎8. 已知函数的一个零点比1大，一个零点比1小，则实数a的取值范围为 ‎______________ .‎ ‎9. 已知 , 则lg108=_______________ .（用 a, b 表示）‎ ‎10.，，且，则的取值集合是______ .‎ ‎11．设是定义在上的奇函数，当时，（为常数），m]则 .‎ ‎12. 若f(x)为R上的偶函数，且在(0，+∞)内是增函数，又f(－3)=0,则 的解集为 .‎ ‎13. 若函数的图像上的任意一点都在函数的下方，则实数的取值范围是 .‎ ‎14．下列判断正确的是 （把正确的序号都填上）．‎ ‎①函数y＝|x－1|与y＝是同一函数； ‎ ‎②若函数在区间上递增，在区间上也递增，则函数必在上递增；‎ ‎③对定义在上的函数，若，则函数必不是偶函数；‎ ‎④函数在上单调递减；‎ ‎⑤若是函数的零点，且，那么.‎ 二、解答题：本大题共6小题，共计90分．‎ ‎15．（本题14分）已知集合A={x|}，B={x|−1≤x<1},‎ ‎（1）求； （2）若全集U=R,求CU(A∪B)；‎ ‎（3）若，且，求的取值范围．‎ ‎[来源:学§科§网]‎ ‎16. (本题14分)计算下列各式的值：‎ ‎(1) ； （2） ‎ ‎17．（本题14分）已知 ‎（1）求的定义域;‎ ‎（2）求使>0成立的x的取值范围.‎ ‎18．（本题16分）已知函数是奇函数，并且函数的图像经过点，‎ ‎（1）求实数的值； ‎ ‎（2）求函数的值域；‎ ‎（3）证明函数在(0,+上单调递减,并写出的单调区间.‎ ‎19．（本题16分）已知二次函数满足 ‎(1)求函数的解析式 ; ‎ ‎(2)若在上恒成立，求实数的取值范围；‎ ‎(3)求当（＞0）时的最大值.‎ ‎20. （本题16分）提高过江大桥的车辆通行能力可改善整个城市的交通状况．在一般情况下，大桥上的车流速度v(单位：千米/小时)是车流密度x(单位：辆/千米)的函数．当桥上的车流密度达到200辆/千米时，造成堵塞，此时车流速度为0；当车流密度不超过20辆/千米时，车流速度为‎60千米/小时．研究表明：当20≤x≤200时，车流速度v是车流密度x的一次函数．‎ ‎(1)当0≤x≤200时，求函数v(x)的表达式；‎ ‎(2)当车流密度x为多大时，车流量(单位时间内通过桥上某观测点的车辆数，单位：辆/小时)‎ f(x)＝x·v(x)可以达到最大，并求出最大值．(精确到1辆/小时)‎ 江苏省江阴市第二中学2012-2013学年高一上学期期中考试数学试题答案 一、填空题：本大题共14小题，每小题5分，共计70分．‎ ‎1、 －1 2、 {3,5}或{1,3,5} 3、 4、（0,2） [来源:学科网]‎ ‎5、 2 6、 7、 8、 （－2,1） ‎ ‎9、 10、 11、 －2 12、（－3,0）∪（1,3）‎ ‎13、 （－4,0 ] 14、 ③ ‎ 二、解答题：本大题共6小题，共计90分．[来源:学科网ZXXK]‎ ‎15、 （ 1 ）‎ ‎（1）=； （ 5 ）‎ ‎ （2）CU(A∪B)= （ 10 ）‎ ‎（3）的取值范围为 （14 ）‎ ‎16、⑴ （ 7 ）‎ ‎⑵－1 （ 14 ）[来源:学+科+网]‎ ‎17、解：（1）‎ ‎ （ 4 ）‎ ‎（2）解:①当a>1时, >0,则，则 因此当a>1时,使的x的取值范围为（0,1）. （ 9 ）‎ ‎②时, ‎ 则解得[来源:学科网ZXXK][来源:Z+xx+k.Com]‎ 因此时, 使的x的取值范围为（-1,0）. （ 14 ）‎ ‎18、解：⑴法一：由题意得 （ 2 ）‎ 解得.经检验为奇函数 （ 5）‎ 法二是奇函数，，即 ‎ ，得，‎ ‎ 所以，得， …………………………3分 又，所以，即 所以. …………………………………………………………5分 ‎（2）法一：=， （ 7 ）‎ ‎ ∴ ∴ ∴‎ ‎∴ （ 10）‎ 法二：由得 （ 7 ）‎ ‎ ∴ 解得 ‎∴ （ 10 ）‎ ‎⑶‎ ‎…………‎ ‎>0‎ ‎∴函数在(0,+上单调递减 ‎∵函数是奇函数，∴在（－∞，0）上也是递减 （ 15 ）‎ ‎∴的单调减区间为（－∞，0），(0,+ （ 16 ）‎ ‎19、（1） （ 5）‎ ‎ ⑵在上的最小值为 （ 8）‎ ‎ ∴ （ 10 ）‎ ‎ ⑶ （ 16 ）‎ ‎20、(1)由题意：当0≤x≤20时，v(x)＝60； （ 3 ）‎ 当20≤x≤200时，设v(x)＝ax＋b，‎ 再由已知得解得 （ 7 ）[来源:学,科,网Z,X,X,K]‎ 故函数v(x)的表达式为v(x)＝ （ 8 ）‎ ‎(2)依题意并由(1)可得f(x)＝ （ 9 ）‎ 当0≤x≤20时，f(x)为增函数，故当x＝20时，其最大值为60×20＝1200； （ 12 ）‎ 当20≤x≤200时，f(x)＝x(200－x)=.[来源:学科网ZXXK]‎ 所以，当x＝100时，f(x)在区间[20,200]上取得最大值.‎ 综上，当x＝100时，f(x)在区间[0,200]上取得最大值≈3333. （ 15 ）‎ 即当车流密度为100辆/千米时，车流量可以达到最大，最大值约为3333辆/小时． （ 16 ）‎