江苏省南京市建邺区2020-2021学年九年级上学期数学期中试卷21-09-81C 14页

【建邺区数学】2020 年九上期中考试试卷 一、选择题（本大题共 6 小题，每小题 2 分，共 12 分。在每小题所给出的四个选项中，恰 有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上） 1、已知 O 的半径是 4cm，点 P 到圆心 O 的距离为 4.5cm，则点 P 与 O 的位置关系是 （ ） A． O 内 B．  O 上 C． O 外 D．以上都有可能 2、某学生六次数学考试的成绩（单位：分）分别为：72、80、77、81、89、81，则这组数 据的众数与中位数分别是（ ） A．81 分、80.5 分 B．89 分、80.5 分 C．81 分、79 分 D．89 分、81 分 3、已知圆锥的底面半径为 2，母线长为 4，则其侧面积为（ ） A．6π B．8π C．16π D．32π 4、一元二次方程 2 3 4 0x x   的根的情况是（ ） A．有一个实数根 B．有两个相等的的实数根 C．有两个不相等的实数根 D．没有实数根 5、如图 PA、PB 是 O 的切线，切点分别为 A、B，点 C 在 AB 上，过 C 作 O 的切线分 别交 PA、PB 于点 D、E，连接 OD、OE，若∠P=50°，则∠DOE 的度数为（ ） A．130° B．50° C．60° D．65° 6、如图，正方形 ABCD 和正三角形 AEF 内接于 O，DC、BC 交 EF 于 G、H，若正方形 ABCD 的边长是 4，则 GH 的长度为（ ） A． 2 2 B． 44 2 33 C． 4 63 D． 8 2 33  第 5 题 第 6 题 E D P O A B C HG FE BD O A C 二、填空题（本大题共 10 小题，每小题 2 分，共 20 分. 不需写出解答过程，请把答案直 接填写在答题卡相应的位置上．．．．．．．．．） 7、写一个一元二次方程使它的解是 0 和 1 ：_____________． 8、设 x1、x2 是方程 2 3 0x x m   的两个根，且 1 2 1 2 2x x x x   ，则 m 的值是______． 9、已知扇形的圆心角为 120°，半径为 3，则这个扇形的面积是______． 10、Rt△ABC 中，∠ACB=90°，AC=4cm，BC=3cm，△ABC 的内切圆半径是______cm． 11、数学期末总评成绩是将平时、期中和期末的成绩按 3：3：4 计算，若小红平时、期中 和期末的成绩分别是 90 分、80 分、100 分，则小红一学期的数学期末总评成绩是 _____________分． 12、若关于 x 的方程 2 0ax bx c   的解为 1 1x   ， 2 3x  ，则方程 2( 1) ( 1) 0a x b x c     的解为________． 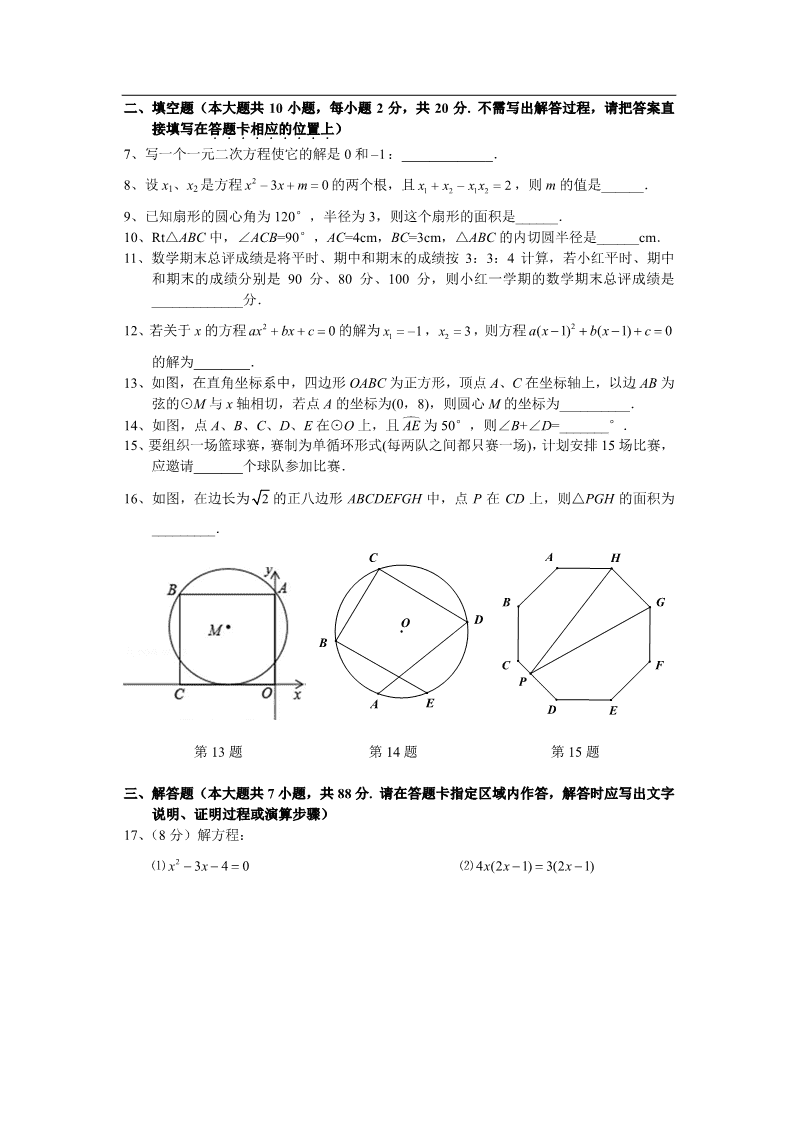13、如图，在直角坐标系中，四边形 OABC 为正方形，顶点 A、C 在坐标轴上，以边 AB 为 弦的⊙M 与 x 轴相切，若点 A 的坐标为(0，8)，则圆心 M 的坐标为__________． 14、如图，点 A、B、C、D、E 在⊙O 上，且  AE 为 50°，则∠B+∠D=_______°． 15、要组织一场篮球赛，赛制为单循环形式(每两队之间都只赛一场)，计划安排 15 场比赛， 应邀请_______个球队参加比赛． 16、如图，在边长为 2 的正八边形 ABCDEFGH 中，点 P 在 CD 上，则△PGH 的面积为 _________． 第 13 题 第 14 题 第 15 题 三、解答题（本大题共 7 小题，共 88 分. 请在答题卡指定区域内作答，解答时应写出文字 说明、证明过程或演算步骤） 17、（8 分）解方程： ⑴ 2 3 4 0x x   ⑵ 4 (2 1) 3(2 1)x x x   O E B C D A C GB F A ED H P 18、（7 分）如图，AB 是 O 的直径，CD 是 O 的弦， 60DBA   ，求∠DCB 的度数． 19、（7 分）某果农 2017 年的年收入为 5 万元，由于党的惠农政策的落实，2019 年年收入 增加到 7.2 万元，求平均每年年收入的增长率． 20、（7 分）如图， O 的弦 AB、CD 的延长线相交于点 P，且 PA=PC．求证 AB=CD． 21、（8 分）已知关于 x 的方程 2 ( 2) 2 0mx m x    ． ⑴若方程有一个根为 2，求 m 的值． ⑵求证：无论 m 取何值，方程总有实数根． 22、（8 分）某社区准备在甲、乙两位射箭爱好者中选出一人参加集训，两人各射了 5 箭， 他们的总成绩（单位：环）相同，甲、乙两人射箭成绩统计表如下． 第 1 次 第 2 次 第 3 次 第 4 次 第 5 次 甲成绩 9 4 7 4 6 乙成绩 7 5 7 a 7 ⑴求 a 的值和甲、乙的方差； ⑵请你从平均数和方差的角度分析，谁将被选中． 23、（9 分）配方法可以用来解一元二次方程，还可以用它来解决一些求最值的问题． 例如： 2 0a  ，所以 2 1 1a   ，即 2 1a  有最小值为 1，此时 0a  ． 再如：  23 1 0a   ，所以  23 1 5 5a    ，即  23 1 5a   有最大值为5，此时 1a   ． ⑴当 x  ______ 时，代数式  22 1 3x   有最______(填“大”或“小”)值，且为______． ⑵当 x  ______ 时，代数式 2 2x x  有最______(填“大”或“小”)值，且为______． ⑶如图，矩形花圃一面靠墙（墙足够长），另外三面所围成的栅栏的总长是 18m，栅栏 如何围能使花圃面积最大？最大面积是多少？ （第23题） 墙 24、（8 分）矩形 ABCD 中，P 在线段．．DC．．上．． ⑴请在图①中利用尺规画出点 P，使得 =90APB  （不写作法，保留作图痕迹）． ⑵①请在图②中利用尺规画出点 P，使得 =60APB  （不写作法，保留作图痕迹）． ② AB m ， 4AD  .若一定存在一点 P，使得 =60APB  ，则 m 的取值范围是 ． 25、（8 分）如图， AB 是 O 的直径，AC 与 O 交于 F，弦 AD 平分 CAB ， DE AC ， 垂足为 E． ⑴判断直线 DE 与 O 的位置关系，并说明理由． ⑵若 O 的半径为 3，若 =60CAB ，求线段 EF． 26、（8 分）某公司组织员工到附近风景区旅游，根据旅行社提供的收费方案，绘制了如图 所示的图像，图中的折线 ABCD 表示人均费用 y(元)与参加人数 x(人)之间的函数关 系．如果该公司支付给旅行社 2800 元，那么参加这次旅游的人数是多少？ C C A B BA D D x y 5530 55 80 DC BA O C E F D OA B 27、（10 分） 【问题提出】 AB、AC、BC 是某区的三条道路，其中 AB=6km，∠BAC=60°，∠B=45°，该区想在 BC 道路边建物资总站点 P，在 AB、AC 道路边分别建物资分站点 E、F，即在线段 BC、AB、 AC 上分别选取点 P、E、F．由于该区工作人员每天要将物资在各物资站点间按 P→E→F →P 的路径进行运输，因此，该区工作人员开始研究线段 PE、EF、FP 之和的最短问题． 图① 图② 【方案设计】 如图②，过点 A 作 AP⊥BC,垂足为 P，分别作 AP 关于 AB、AC 对称线段 AP1，AP2．连接 P1P2，P1P2 与 AB、AC 交于 E、F，此时 PE、EF、FP 距离之和最短．试求 PE+EF+FP 的 最小值． 【拓展延伸】 该区的三条道路改为如图所示的 AB、AC、弧 BC 的方式，其中 AB=6km，AC=3km， ∠BAC=60°，弧 BC 为 60°．分别在弧 BC、AB、和 AC 上选取点 P、E、F．使得线段 PE、 EF、FP 之和最短，画出图形确定 P、E、F 的位置，并求 PE+EF+FP 的最小值． 图③ F E P2 P1 B C A A CB P A CB 【建邺区数学】2020 九上期中考试答案 一、选择题（本大题共 6 小题，每小题 2 分，共 12 分。在每小题所给出的四个选项中，恰 有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上） 题号 1 2 3 4 5 6 答案 C A B D D A 第 6 题解析: 连接 AC 交 EF 于 M，由正方形 ABCD， 可知△ACD 为等腰直角三角形，所以 AC= 4 2 ， r= 2 2 ．等边三角形 AEF 中，O 为中心，则 2 2AO  ， 22 OFOM   ，所以 3 2AM  ． Rt△CMG 中，CM=MG= 2 ，则 GH= 2 2 ． 二、填空题（本大题共 10 小题，每小题 2 分，共 20 分. 不需写出解答过程，请把答案直 接填写在答题卡相应的位置上．．．．．．．．．） 第 16 题解析：作正八边形外接圆⊙O ∴ 1 4 360 902 8HGD       ， 1 2 360 452 8FGD       ∵正八边形 ABCDEFGH ∴CD∥HG ∴S△HGP=S△HGD 过点 F 作 FM⊥GD 于点 M，过点 E 作 EN⊥GD 于点 N Rt△GMF 中，∠FGD=45°，GF= 2 ∴GM=1 同理 DN=1 又 MN=EF= 2 ∴GD=1+ 2 +1= 2 +2 ∴S△HGP=S△HGD= 1 2 HG GD = 1 2 2+22  （ ）= 2+1 题号 7 8 9 10 11 答案 2 0x x  1 3π 1 91 题号 12 13 14 15 16 答案 1 0x  ， 2 4x  ( 4 ，5) 155 6 2 1 N M C GB F A ED H P M HG FE BD O C A 三、解答题 17、⑴ 1 4x  ， 2 1x   ⑵ 1 3 4x  ， 2 1 2x  18、解：∵AB 是 O 的直径 ∴ 90ADB   即： Rt ABD△ 中， 90ADB   ， 60DBA   ∴ 180 30DAB DBA ADB         ∵  BD BD ∴ 30DCB DAB     19、解：设平均每年收入的增长率为 x ． 根据题意得：  25 1 7.2x  ， 解得： 1 0.2=20%x  ， 2 2.2x   （舍负） 答：平均每年收入的增长率为 20%． 20、证明： 法一：连接 AC 、BD， ∵PA=PC， ∴∠PAC=∠PCA， ∵四边形 ACDB 为 O 的内接四边形， ∴ 180PAC BDC     180PCA ABD     ， ∵∠PAC=∠PCA， ∴ BDC ABD   ， ∵ 180PBD ABD     180PDB BDC     ， ∴ PBD PDB   ， ∴ PB PD ， ∵ AB AP PB  CD PC PD  且 PA PC ， ∴ AB CD 法二：连接 AC、OA、OB、OC、OD， ∵PA=PC， ∴∠PAC=∠PCA， ∵∠PAC= 1 2 ∠BOC，∠PCA 1 2 ∠AOD， D B PO A C ∴∠BOC＝∠AOD， ∴  AD BC ， ∴    AD BD BC BD   ，即  AB CD ， ∴ AB CD 21、⑴解：令 2x  ，得： 4 2 4 2 0m m    ，所以 1m  ； ⑵证明： ①当 0m  时，该方程为一元二次方程． a m ， 2b m   ， 2c   22 4 2 4 2b ac m m     2 4 4m m    22 0m  ≥ ∴当 0m  时，该方程有两个实数根． ②当 0m  时，该方程为一元一次方程． 原方程变为 2 2 0x   ，解得： 1x  ∴当 0m  时，该方程有解． ∴综上所述，无论 m 取何值，方程总有实数根． 22、(1) 4a  ； 2 3.6s 甲 ， 2 1.6s 乙 解析：∵甲乙总成绩相同 ∴  9+4+7+4+6 7 5 7 7 4a       9+4+7+4+6= = =65x x甲 乙          2 2 2 2 22 1 9 6 4 6 7 6 4 6 6 6 3.65s              甲          2 2 2 2 22 1 7 6 5 6 7 6 4 6 7 6 1.65s              乙 (2)选择乙． 由(1)得 = =6x x甲 乙 ，甲乙两人平均数相等； 2 3.6s 甲 ， 2 1.6s 乙 ，甲的方差大于乙的方 差，说明甲的成绩波动较大，所以乙将被选中． 23、(1) 1，小，3  22 1 0x   ，  22 1 +3 3x   有最小值，当 1x  取到． (2) 1 ，大，1 配方得  22 2 1 1x x x      ,  21 0x   ，  21 1 1x    有最大值，当 1x   取到． (3)宽为 9 2 m 时，最大面积是 281m2 设与墙垂直的边为 xm，则平行于墙的边为 18 2x m．   2 18 2 2 18 9 812 2 2 S x x x x x              ∵ 92 02x       ； 9 81 812 2 2 2x         ，当 9 2x  ， S 有最大值 81 2 ． 24、⑴ 如图：点 1 2P P、 即为所求 ⑵① 如图：点 1 2P P、 即为所求 P2P1 C BA D P2P1 C A B D ② 8 3 4 33 m  提示：当 CD 与圆相切时 m 取最小值 8 3 3 ； 当圆为矩形 ABCD 的外接圆时 m 取最大值 4 3 25、⑴答：直线 DE 与 O 相切，理由如下： 如图：连接 OD ∵ AD 平分 CAB ∴ =CAD BAD  ∵OA OD ∴ BAD ADO   ∴ =CAD ADO  ∴OD∥AC ∴ 180DEA EDO    ∵ DE AC ∴ 90DEA   ∴ 90EDO   即 DE OD ∵D 在 O 上 ∴DE 与 O 相切于点 D ⑵解：如图：过点O 点作OG AF 交 AF 于点G ∵ =60CAB ， 3OA  ∴ 1 3 2 2AG FG OA   ∴AF=3 ∵OD∥AF，OD=AF C E F D O BA C G E F D OA B C BA D C A B D ∴四边形 OAFD 是平行四边形 ∴DF∥OA，DF=OA=3 ∴ = 60DFE BAC    ∴ 1 3 2 2EF DF  26、解：①当0 30x  时 ∵30 80 2400 2800   ∴旅游人数大于 30 人 ②当30 55x  时 设直线 BC 表达式为 y kx b  （ 0k  ） 将  30,80B 、  55,55C 代入，得 30 80 55 55 k b k b      解得： 1 110 k b     ∴ 110(30 55)y x x     由题意得，  110 2800x x    解得： 1 240, 70x x  （舍去） ∴人数为 40 人 ③当 55x  时，55 55 3025 2800  ＞ ∴旅游人数小于 55 人 答：综上，这次旅游参加人数为 40 人． 27、【方案设计】 AP BC∵ ⊥ 90APB  ∴∠ 45BAP B  ∴∠ ∠ BP AP∴ 2 2 2 36BP AP AB  ∵ 3 2AP ∴ 由对称知， 1 2 3 2AP AP AP   ， 1 2,P AE PAE PAF P AF ∠ ∠ ∠ ∠ 60BAC  ∵∠ 1 2 2 2 120P AP PAE PAF   ∴∠ ∠ ∠ 过点 A 作 AG⊥ 1 2PP ，垂足为 G 1 2AP AP∵ 1 2 1 230 ,P P PG P G   ∴∠ ∠ 1 1 3 22 2AG AP ∴ 2 2 1 1 3 6 2PG AP AG  ∴ 1 2 12 3 6PP PG ∴ ∴ PE EF FP  最小值为3 6km ． 【拓展延伸】 如图，补全扇形 BOC ∵弧 BC 的度数是 60 度 ∴ 60BOC  ∠ 在弧 BC 上任取一点 P 在 APO△ 中， AP AO PO  当 A、P、O 三点共线时， AP AO PO  ，即取最小值，故连接 AO，交 BC 于点 P 取 AB 中点 D ，连接CD 则 3AD BD AC   又∵ DAC  60° ∴ ADC△ 为等边三角形 ∴ ADC  60°，CD AD BD  ∴ 120BDC   ∴ 30ABC   ∴ 90ACB   ∵OB OC ， 60BOC   ∴ BOC△ 为等边三角形 G F E P2 P1 A CB P ∴ 60OBC  ，OB BC ∴ 90ABO   2 2 3 3BC AB AC   ∴ 3 3OB  ∴ 2 2+ 3 7AO AB BO  ∴ 3 7 3 3AP AO PO    分别作 AP 关于 AB ， AC 对称线段 1AP ， 2AP ，交 AB ， AC 于 E ， F 则 1 2PP 为 PE EF FP  最小值 可知 1 2 3 7 3 3AP AP AP    同“方案设计”可求 1 2 3 21 9PP   ∴ PE EF FP  最小为(3 21 9) km． D F E P2 P1 P O A B C