人教版九年级数学下册 27.3位似 同步测试 23页

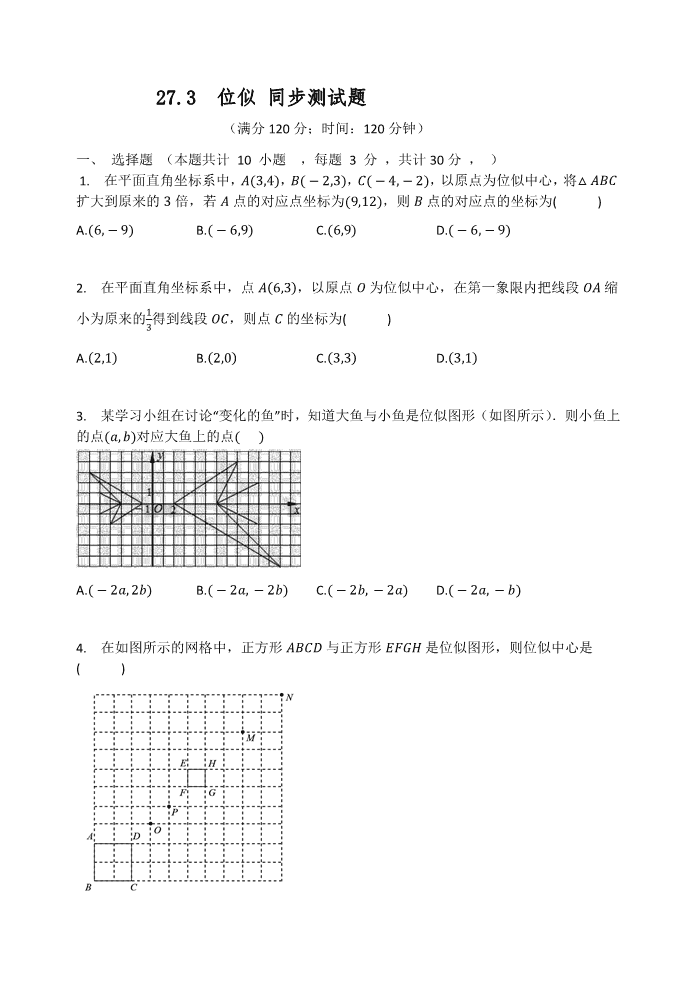
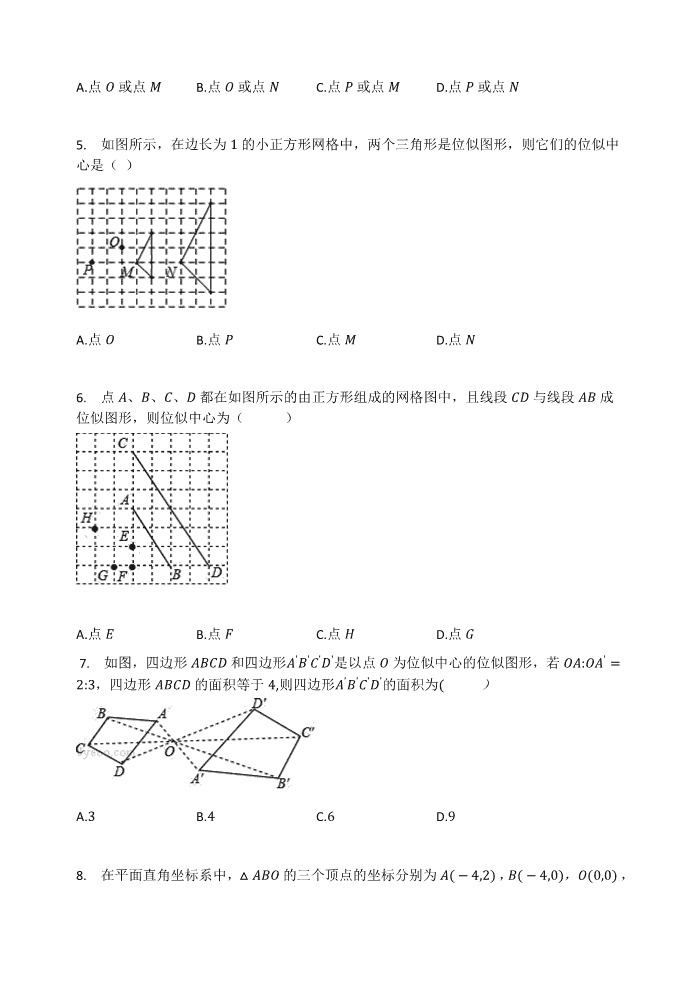
27.3位似同步测试题（满分120分；时间：120分钟）一、选择题（本题共计10小题，每题3分，共计30分，）1.在平面直角坐标系中，옠ɰˈ，െ옠ˈ，ɰ옠െˈ，以原点为位似中心，将扩大到原来的倍，若点的对应点坐标为െ옠ʹെˈ，则点的对应点的坐标为()A.െ옠െˈB.െ옠െˈC.െ옠െˈD.െ옠െˈ2.在平面直角坐标系中，点െ옠，以原点为位似中心，在第一象限内把线段缩ʹ小为原来的得到线段，则点的坐标为()A.െ옠ʹB.െ옠䁜C.옠D.옠ʹ3.某学习小组在讨论“变化的鱼”时，知道大鱼与小鱼是位似图形（如图所示）．则小鱼上的点ᦙ옠ˈ对应大鱼上的点ˈA.െᦙ옠െˈB.െᦙ옠െˈC.െ옠െᦙˈD.െᦙ옠ˈ4.在如图所示的网格中，正方形形与正方形正方形是位似图形，则位似中心是() A.点或点B.点或点C.点或点D.点或点5.如图所示，在边长为ʹ的小正方形网格中，两个三角形是位似图形，则它们的位似中心是（）A.点B.点C.点D.点6.点、、、形都在如图所示的由正方形组成的网格图中，且线段形与线段成位似图形，则位似中心为（）A.点B.点正C.点形D.点方7.如图，四边形形和四边形形是以点为位似中心的位似图形，若〵െ〵，四边形形的面积等于ɰ,则四边形形的面积为）A.B.ɰC.െD.െ8.在平面直角坐标系中，的三个顶点的坐标分别为ɰ옠െˈ，ɰ옠䁜ˈ，䁜옠䁜ˈ， 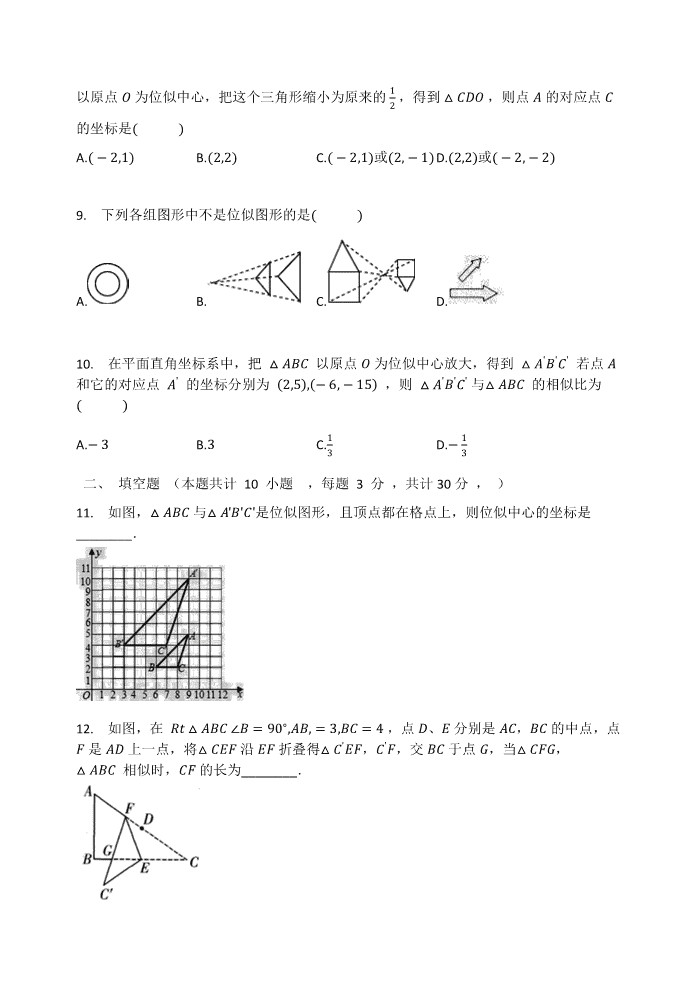ʹ以原点为位似中心，把这个三角形缩小为原来的，得到形，则点的对应点െ的坐标是ˈA.െ옠ʹˈB.െ옠െˈC.െ옠ʹˈ或െ옠ʹˈD.െ옠െˈ或െ옠െˈ9.下列各组图形中不是位似图形的是ˈA.B.C.D.10.在平面直角坐标系中，把以原点为位似中心放大，得到若点和它的对应点的坐标分别为െ옠㈠옠െ옠ʹ㈠，则与的相似比为ˈʹʹA..BC.D.二、填空题（本题共计10小题，每题3分，共计30分，）11.如图，与是位似图形，且顶点都在格点上，则位似中心的坐标是________．12.如图，在െ䁜옠옠옠ɰ，点形、分别是，的中点，点正是形上一点，将正沿正折叠得正，正，交于点方，当正方，相似时，正的长为________． 13.在平面直角坐标系中，三个顶点的坐标分别为െ옠ɰˈ，ɰ옠䁜ˈ，䁜옠䁜ˈ．以ʹ原点为位似中心，把这个三角形缩小为原来的，得到形，则点的对应点的坐െ标是________．14.大矩形的周长是与它位似的小矩形的െ倍，小矩形的面积是㈠െ，大矩形的长为㈠，则大矩形的宽为________．15.已知四边形形各顶点的坐标分别为െ옠െ，ɰ옠െ，െ옠െ，形െ옠ɰ，以䁜为位似中心，作四边形形位似与四边形形位似，对应边的比为ʹ，则点、、、形െ的对应点的坐标分别为________，________，________，________.ʹ16.把一个三角形变成和它位似的另一个三角形，若边长缩小到倍，则面积缩小到原来െ的________倍．ʹ17.如图，五边形形与五边形形是位似图形，且位似比为．若五边形形െ的，面积为െ䁜െ，那么五边形形的面积为________．18.在中，옠െ䁜，将沿方向平移，得到，以为正位似中心，作形与位似，位似比为ʹ〵െ，正为的中点，连接形正,正,则形正的值为________.19.如图，与形正是位似图形，位似比为െ〵，已知ɰ，则形的长为 ________．20.如图，的顶点在格点上，且点㈠옠ʹˈ，点ʹ옠െˈ．以原点为位似中心，位似比为െ，在第一象限内将放大，画出________放大后的图形并写出各顶点坐标．三、解答题（本题共计6小题，共计60分，）21.已知：在坐标平面内，三个顶点的坐标分别为䁜옠ˈ，옠ɰˈ，െ옠െˈ．（正方形网格中，每个小正方形的边长是ʹ个单位长度）请以点为位似中心，在网格中画出ʹʹʹ，使ʹʹʹ与位似，且位似比为െ〵ʹ，并求出ʹʹʹ的面积． 22.如图，已知是坐标原点，，的坐标分别为옠ʹˈ，െ옠ʹˈ.ʹˈ在轴的左侧以为位似中心作的位似三角形形㌳（要求：新图与原图的相似比为െ〵ʹˈ；െˈ分别写出，的对应点，形的坐标；ˈ若线段上有一点옠ꀀˈ，则点在上的对应点的坐标为________.23.如图，在平面直角坐标系中，െ옠ʹˈ，ʹ옠െˈ．ʹˈ画出向左平移െ个单位长度，再向上平移ʹ个单位长度后的ʹʹʹ;െˈ以原点为位似中心，在轴的右侧画出的一个位似െെ，使它与的相似比为െ〵ʹ;ˈ判断ʹʹʹ与െെ是否关于某一点为位似中心的位似图形？若是，请在图中标出位似中心,并写出点的坐标. 24.如图，已知是坐标原点，、两点的坐标分别为옠ʹˈ、െ옠ʹˈ．ʹ以点为位似中心在轴的左侧将放大到两倍（即新图与原图的相似比为െ)，画出图形；െ分别写出、两点的对应点、的坐标．25.如图，形，相交于点，连结，，形，形，形.ʹˈ求证：形；െˈ形与是不是位似图形？并说明理由；形옠ɰ形，⸰若ˈ，求的长． 26.如图，已知是原点，、两点的坐标分别为옠ʹˈ，െ옠ʹˈ.ʹˈ以点为位似中心，在轴的左侧将扩大为原来的两倍（即新图与原图的相似比为െ），画出图形并写出点，的对应点的坐标；െˈ如果内部一点的坐标为ᦙ옠ˈ，写出点的对应点的坐标． 参考答案与试题解析一、选择题（本题共计10小题，每题3分，共计30分）1.【答案】B【解答】解：∵以原点为位似中心，将放大为原来的倍，点옠ɰˈ的对应点是െ옠ʹെˈ，则点െ옠ˈ的对应点为െ옠െˈ.故选.2.【答案】A【解答】解：在平面直角坐标系中，点െ옠，以原点为位似中心，ʹ在第一象限内把线段缩小为原来的得到线段，ʹʹ则点的对应点的坐标为െ옠ˈ，即点坐标为െ옠ʹ.故选.3.【答案】B【解答】解：根据图形可得，两个图形的位似比是ʹ〵െ，∴对应点是െᦙ옠െˈ.故选．4.【答案】D【解答】解：如图，连接方，，正形，形交于点；连接，正，形形，方并分别延长交于点, 则位似中心为点或点.故选形.5.【答案】B【解答】如图所示：两个三角形的位似中心是：点．故选：．6.【答案】B【解答】解：点、、、形都在如图所示的由正方形组成的网格图中，且线段形与线段成位似图形，则位似中心为点正， 故选㌳7.【答案】D【解答】解：∵四边形形和形是以点为位似中心的位似图形，〵െ〵，∴四边形形与四边形形的面积比为：ɰ〵െ.四边形形的面积等于ɰ,四边形形的面积为െ.故选形.8.【答案】C【解答】ʹ解：∵点ɰ옠െˈ，且相似比为，െ∴当形与在轴同侧时，点的坐标为െ옠ʹˈ，当形与在轴异侧时，点的坐标为െ옠ʹˈ.故选.9.【答案】D【解答】解：根据位似图形的定义，可得，，是位似图形，与的位似中心是交点，的位似中心是圆心；形不是位似图形．故选形．10. 【答案】B【解答】解：和关于原点位似，且点和它的对应点的坐标分别为െ옠㈠옠െ옠ʹ㈠，对应点的坐标乘以，∴与的相似比为.故选.二、填空题（本题共计10小题，每题3分，共计30分）11.【答案】【解答】解：由题图可知，直线与直线的交点坐标为，所以位似中心的坐标为．故答案为：.12.【答案】ɰ或െ㌳⸰【解答】解：①当正方时，将正沿正折叠得正，∴옠െ，∴sinsin，方∴，∴方ʹ㌳െ， ∵正方，方正∴，即㌳െ正，ɰ㈠∴正ɰ；②当方正时，如图，将正沿正折叠得正，∴ʹെɰ㈠，∴形正形，形∵sinsin，െ∴形െ，㈠㈠∴形െ形െ⸰，㈠∴正正形൅形正ʹ㌳െ൅ʹ㌳െെ㌳⸰.综上所述，当正方与相似时，正的长为ɰ或െ㌳⸰.故答案为∶ɰ或െ㌳⸰.13.【答案】ʹ옠െˈ或ʹ옠െˈ【解答】ʹ解：以原点为位似中心，把这个三角形缩小为原来的，点的坐标为െ옠ɰˈ，െʹʹʹʹ∴点的坐标为െ옠ɰˈ或െ옠ɰˈ，即ʹ옠െˈ或ʹ옠െˈ.െെെെ故答案为：ʹ옠െˈ或ʹ옠െˈ.14.【答案】ɰ【解答】解：∵大矩形与小矩形位似， ∴位似比等于相似比为െ〵ʹ．∵其对应的面积比等于相似比的平方为ɰ〵ʹ，∴大矩形面积为െ䁜െ．∴大矩形的宽为ɰ．故大矩形的宽为ɰ．15.【答案】ʹ옠,െ옠ʹ,옠ʹ,옠െ【解答】解：如图，连接、、、形，分别取它们的中点，，，形，即四边形形即为所求.∴ʹ옠，െ옠ʹ，옠ʹ，形옠െ.故答案为：ʹ옠；െ옠ʹ；옠ʹ；옠െ.16.【答案】ʹɰ【解答】解：∵把一个三角形变成和它位似的另一个三角形，若边长缩小了െ倍∴位似比等于ʹ〵െ∴面积比等于ʹ〵ɰʹ∴面积缩小到原来的倍．ɰ17.【答案】㈠【解答】 ʹ解：∵五边形形与五边形形是位似图形，且位似比为，െ∴五边形形的面积与五边形形的面积比为：ʹ〵ɰ，∵五边形形的面积为െ䁜െ，∴五边形形的面积为：㈠．故答案为：㈠．18.【答案】ʹ或㈠【解答】解：设െܥ，①如图ʹ，当点形在上时，∵，∴െܥ，∵正为的中点，∴正ܥ，则正െ൅正െ㈠ܥ，形ʹ又∵形，且，െ∴形ܥ，则正െܥ，∴形正形െ൅正െ㈠ܥ，正㈠ܥ∴ʹ；形正㈠ܥ②如图െ，当点形在延长线上时， 由①知正െ൅正െ㈠ܥ，形正形ܥ，正㈠ܥ∴㈠.形正ܥ故答案为：ʹ或㈠.19.【答案】െ【解答】解：∵与形正是位似图形，位似比为െ〵，∴〵形െ〵，∴形െ．故答案为：െ．20.【答案】【解答】解：如图所示：即为所求，ʹ䁜옠െˈ，ʹ䁜옠െˈ，െ옠ɰˈ． 三、解答题（本题共计6小题，每题10分，共计60分）21.【答案】解：如图所示：ʹʹʹ即为所求，ʹʹʹ的面积为：ʹʹʹɰെെെെɰെɰʹ䁜．െെെ【解答】解：如图所示：ʹʹʹ即为所求，ʹʹʹ的面积为： ʹʹʹɰെെെെɰെɰʹ䁜．െെെ22.【答案】解：ʹˈ如图：形即为所求.െˈ由图可知：〵െ옠െ，形〵ɰ옠െ㌳െ옠െꀀ【解答】解：ʹˈ如图：形即为所求.െˈ由图可知：〵െ옠െ，形〵ɰ옠െ㌳ˈ根据原点位似的特点可知െ옠െꀀ.故答案为：െ옠െꀀ.23. 【答案】解：如图所示：如图：如图所示，与是关于为位似中心的位似图形.【解答】解：如图所示： 如图：如图所示，与是关于为位似中心的位似图形.24.【答案】解：是所求的三角形； 的坐标是，的坐标是．【解答】解：是所求的三角形；的坐标是，的坐标是．25.【答案】ʹˈ证明：形，形，形；െˈ解：形与不是位似图形，因为它们的对应边不平行；ˈ形，，形又形，形，，形形⸰即，ɰ解得，െ．【解答】ʹˈ证明：形，形，形；െˈ解：形与不是位似图形， 因为它们的对应边不平行；ˈ形，，形又形，形，，形形⸰即，ɰ解得，െ．26.【答案】解：ʹˈ如图，ʹʹ为所作，点ʹ，ʹ点的坐标分别为െ옠െˈ，ɰ옠െˈ；െˈ把点的横纵坐标分别乘以െ即可得到ʹ的坐标，所以点的对应点的坐标为െᦙ옠െˈ.【解答】解：ʹˈ如图，ʹʹ为所作，点ʹ，ʹ点的坐标分别为െ옠െˈ，ɰ옠െˈ；െˈ把点的横纵坐标分别乘以െ即可得到ʹ的坐标， 所以点的对应点的坐标为െᦙ옠െˈ.