人教版九年级数学上册同步练习题及解析：弧长和扇形面积（1） 5页

24.4弧长和扇形面积（第一课时）◆随堂检测1．钟表的轴心到分针针端的长为5cm，那么经过40分钟，分针针端转过的弧长是（）A.B.C.D.2.如果圆柱的母线长为5cm，底面半径为2cm，那么这个圆柱的侧面积是（）A.B.C.D.3．小明要制作一个圆锥模型，其侧面是由一个半径为9cm，圆心角为240°的扇形纸板制成的，还需用一个圆形的纸板做底面，那么这块圆形纸板得直径为多少？4.在一块空旷的草地上有一根柱子，柱子上拴着一条长5m的绳子，绳子的另一端拴着一头牛，如图所示.(1)这头牛吃草的最大活动区域有多大?(2)如果这头牛只能绕柱子转过n°角，那么它的最大活动区域有多大?◆典例分析如图，A是半径为12cm的圆O上的一点，点B是OA延长线上的一点，且AB=OA，点P从A出发，以的速度沿圆周逆时针运动，当点P运动的时间为2s时，判断直线BP与圆O的位置关系，并说明理由.分析：这是一道运动类型的综合题目,首先要根据条件(时间为2s)画出相应的图形,判断直线BP与圆O相切,然后再利用判定定理进行证明.所以所以直线BP与圆O相切解：直线BP与圆O相切.理由如下:连接BP,OP,PA.∵=,∴,即.∵因为A0=PO,∴△为等边三角形，∴,OA=PA.∵OA=AB，OA=PA，∴AB=PA.∴，∵，∴,∴.∴所以BP为圆O的切线. 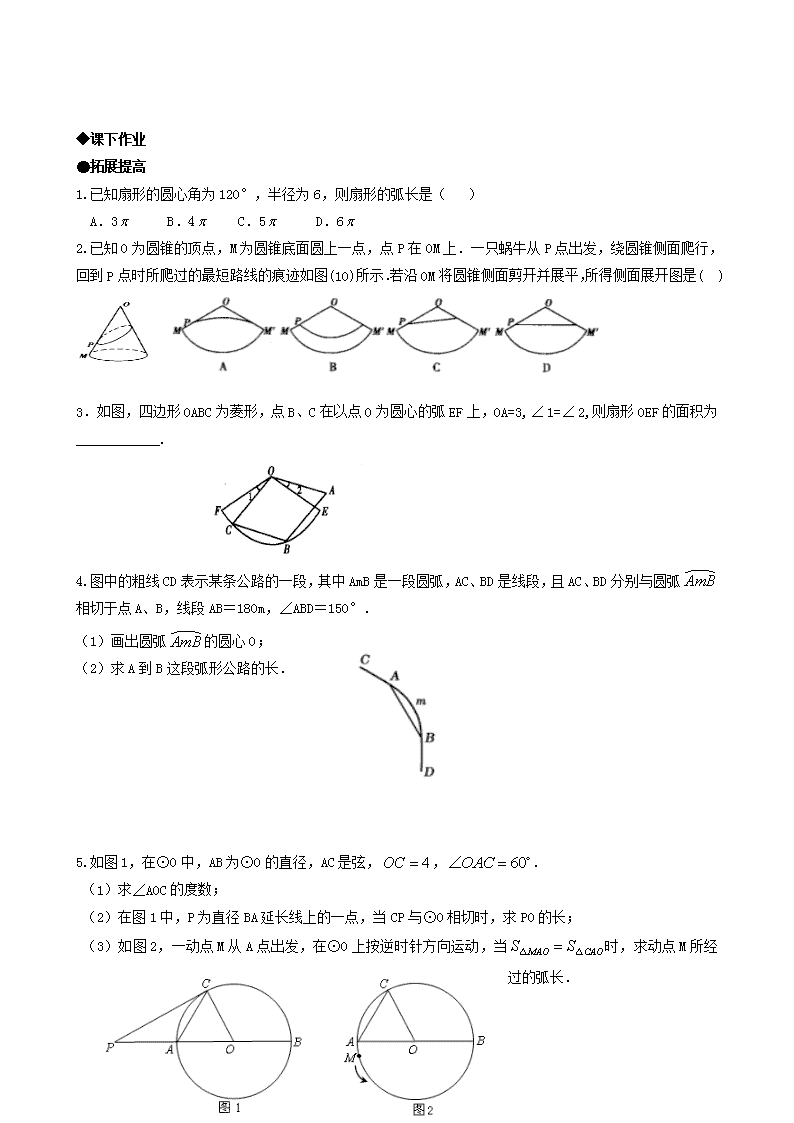◆课下作业●拓展提高1.已知扇形的圆心角为120°，半径为6，则扇形的弧长是（）A．3B．4C．5D．62.已知O为圆锥的顶点，M为圆锥底面圆上一点，点P在OM上．一只蜗牛从P点出发，绕圆锥侧面爬行，回到P点时所爬过的最短路线的痕迹如图(10)所示．若沿OM将圆锥侧面剪开并展平，所得侧面展开图是()3．如图，四边形OABC为菱形，点B、C在以点O为圆心的弧EF上，OA=3,1=2,则扇形OEF的面积为____________.4.图中的粗线CD表示某条公路的一段，其中AmB是一段圆弧，AC、BD是线段，且AC、BD分别与圆弧相切于点A、B，线段AB＝180m，∠ABD＝150°．（1）画出圆弧的圆心O；（2）求A到B这段弧形公路的长．5.如图1，在⊙O中，AB为⊙O的直径，AC是弦，，．（1）求∠AOC的度数；（2）在图1中，P为直径BA延长线上的一点，当CP与⊙O相切时，求PO的长；（3）如图2，一动点M从A点出发，在⊙O上按逆时针方向运动，当时，求动点M所经过的弧长． ●体验中考1.（2009年，河池）如图，，切⊙O于，两点，若，⊙O的半径为，则阴影部分的面积为___________.APBO2.（2009年,台州市）如图，三角板中，，，．三角板绕直角顶点逆时针旋转，当点的对应点落在边的起始位置上时即停止转动，则点转过的路径长为__________.CAB参考答案：◆随堂检测1.B.弧长是.2.D.圆柱侧面展开图图是矩形，面积为2×2×5＝20.3.解：，解得：. 4.解:(1).(2).◆课下作业●拓展提高1.B.2.D.3..4.解：（1）如图，过A作AO⊥AC，过B作BO⊥BD，AO与BO相交于O，O即圆心．（2）∵AO、BO都是圆弧的半径，O是其圆心，∴∠OBA＝∠OAB＝150°-90°＝60°．∴△AOB为等边三角形．∴AO＝BO＝AB＝180．∴(m)．∴A到B这段弧形公路的长为m．5．解：（1）∵在△ACO中，，OCOA,∴△ACO是等边三角形,∴∠AOC60°（2）∵CP与⊙O相切，OC是半径．∴CP⊥OC,∴∠P90°-∠AOC30°∴PO2CO8.（3）如图2，①作点关于直径的对称点，连结，OM1．易得，.∴.∴当点运动到时，，此时点经过的弧长为．②过点作∥交⊙O于点，连结，，易得．∴,∴或.∴当点运动到时，，此时点经过的弧长为．③过点作∥交⊙O于点，连结，，易得∴，∴或. ∴当点运动到时，，此时点经过的弧长为．④当点运动到时，M与C重合，，此时点经过的弧长为或．●体验中考1．.2..注意正确应用弧长的计算公式.