咸宁市2020年中考数学试题及答案 34页

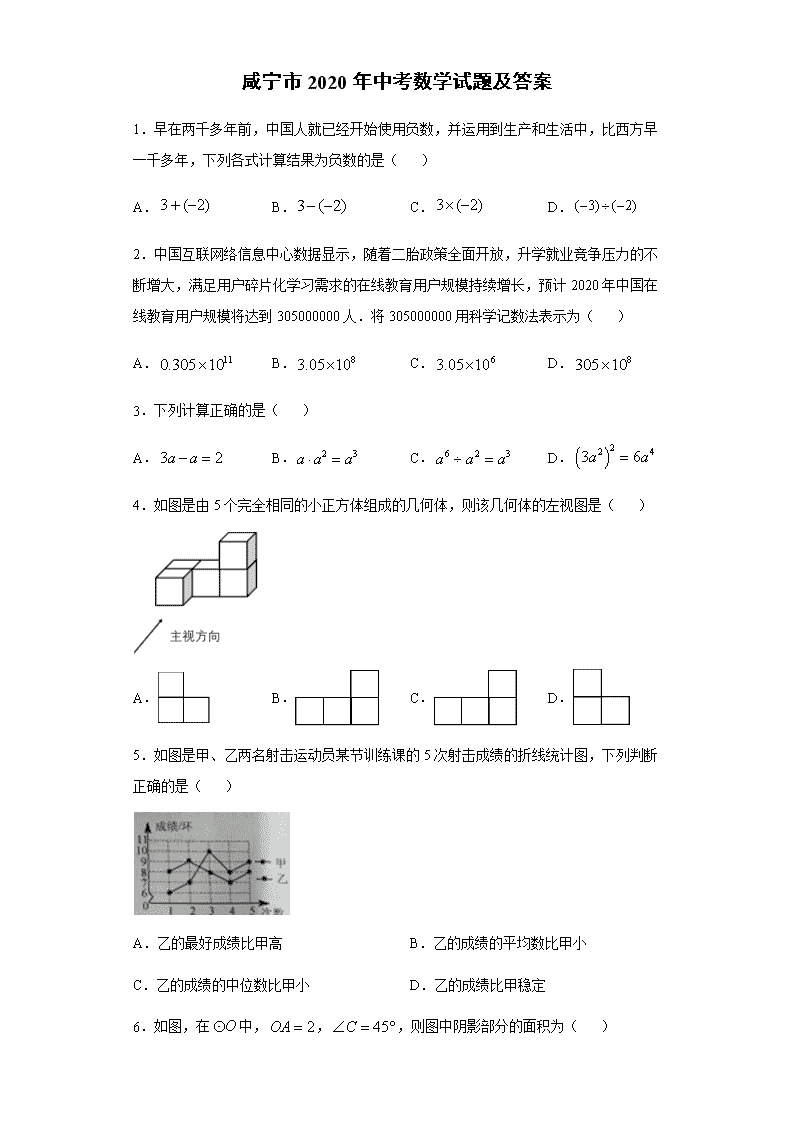
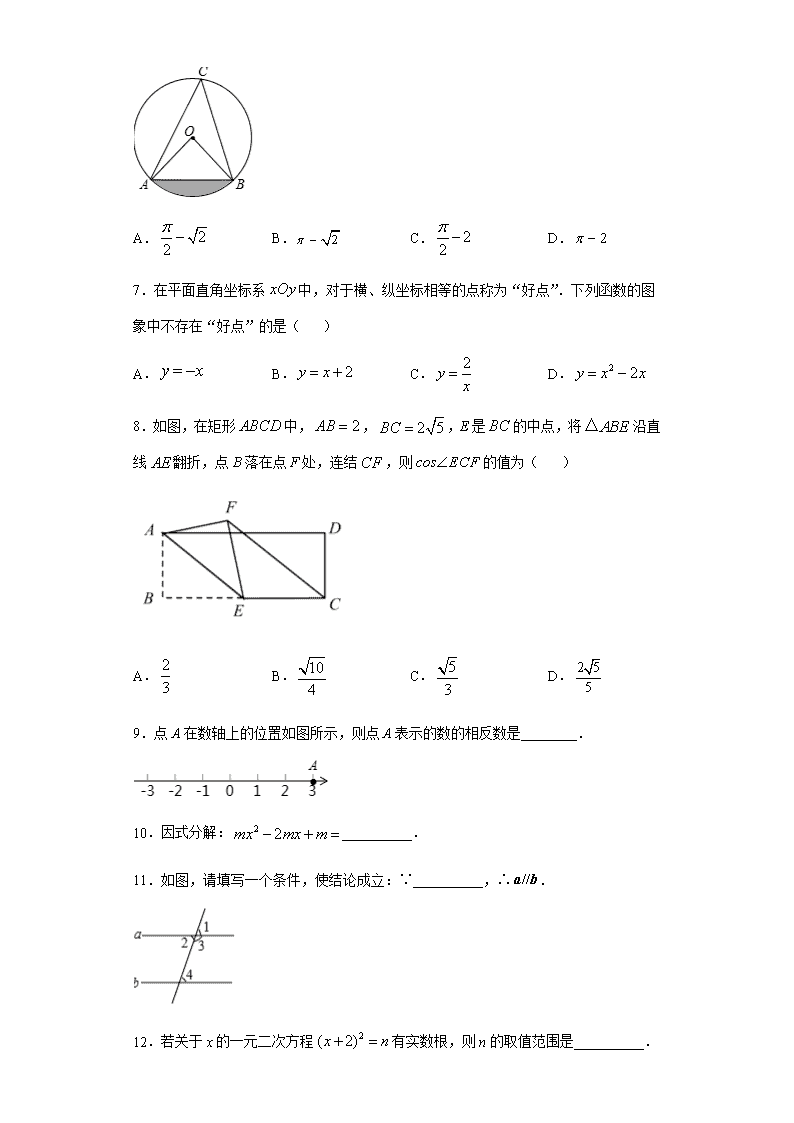
咸宁市2020年中考数学试题及答案1．早在两千多年前，中国人就已经开始使用负数，并运用到生产和生活中，比西方早一千多年，下列各式计算结果为负数的是（）A．B．C．D．2．中国互联网络信息中心数据显示，随着二胎政策全面开放，升学就业竞争压力的不断增大，满足用户碎片化学习需求的在线教育用户规模持续增长，预计2020年中国在线教育用户规模将达到305000000人．将305000000用科学记数法表示为（）A．B．C．D．3．下列计算正确的是（）A．B．C．D．4．如图是由5个完全相同的小正方体组成的几何体，则该几何体的左视图是（）A．B．C．D．5．如图是甲、乙两名射击运动员某节训练课的5次射击成绩的折线统计图，下列判断正确的是（）A．乙的最好成绩比甲高B．乙的成绩的平均数比甲小C．乙的成绩的中位数比甲小D．乙的成绩比甲稳定6．如图，在中，，，则图中阴影部分的面积为（） A．B．C．D．7．在平面直角坐标系中，对于横、纵坐标相等的点称为“好点”．下列函数的图象中不存在“好点”的是（）A．B．C．D．8．如图，在矩形中，，，E是的中点，将沿直线翻折，点B落在点F处，连结，则的值为（）A．B．C．D．9．点A在数轴上的位置如图所示，则点A表示的数的相反数是________．10．因式分解：__________．11．如图，请填写一个条件，使结论成立：∵__________，∴．12．若关于x的一元二次方程有实数根，则n的取值范围是__________． 13．某校开展以“我和我的祖国”为主题的“大合唱”活动，七年级准备从小明，小东、小聪三名男生和小红、小慧两名女生中各随机选出一名男生和一名女生担任领唱，则小聪和小慧被同时选中的概率是________．14．如图，海上有一灯塔P，位于小岛A北偏东60°方向上，一艘轮船从北小岛A出发，由西向东航行到达B处，这时测得灯塔P在北偏东30°方向上，如果轮船不改变航向继续向东航行，当轮船到达灯塔P的正南方，此时轮船与灯塔P的距离是________．（结果保留一位小数，）15．按一定规律排列的一列数：3，，，，，，，，…，若a，b，c表示这列数中的连续三个数，猜想a，b，c满足的关系式是__________．16．如图，四边形是边长为2的正方形，点E是边上一动点（不与点B，C重合），，且交正方形外角的平分线于点F，交于点G，连接，有下列结论：①；②；③；④的面积的最大值为1．其中正确结论的序号是_____________．（把正确结论的序号都填上） 17．（1）计算：；（2）解不等式组：18．如图，在中，以点B为圆心，长为半径画弧，交于点E，在上截取，连接．（1）求证：四边形是菱形；（2）请用无刻度的直尺在内找一点P，使（标出点P的位置，保留作图痕迹，不写作法）19．如图，已知一次函数与反比例函数的图象在第一、三象限分别交于，两点，连接，．（1）求一次函数和反比例函数的解析式；（2）的面积为______；（3）直接写出时x的取值范围．20．随着科技的进步和网络资源的丰富，在线阅读已成为很多人选择的阅读方式．为了解同学们在线阅读情况，某校园小记者随机调查了本校部分同学，并统计他们平均每天的在线阅读时间t（单位：），然后利用所得数据绘制成如下不完整的统计图表． 在线阅读时间频数分布表组别在线阅读时间t（人数）A4B8CaD16E2根据以上图表，解答下列问题：（1）这次被调查的同学共有______人，______，_____；（2）求扇形统计图中扇形D的圆心角的度数；（3）若该校有950名学生，请估计全校有多少学生平均每天的在线阅读时间不少于?21．如图，在中，，点O在上，以为半径的半圆O交于点D，交于点E，过点D作半圆O的切线，交于点F． （1）求证：；（2）若，，，求半圆O的半径长．22．5月18日，我市九年级学生安全有序开学复课．为切实做好疫情防控工作，开学前夕，我市某校准备在民联药店购买口罩和水银体温计发放给每个学生．已知每盒口罩有100只，每盒水银体温计有10支，每盒口罩价格比每盒水银体温计价格多150元．用1200元购买口罩盒数与用300元购买水银体温计所得盒数相同．（1）求每盒口罩和每盒水银体温计的价格各是多少元？（2）如果给每位学生发放2只口罩和1支水银体温计，且口罩和水银体温计均整盒购买．设购买口罩m盒（m为正整数），则购买水银体温计多少盒能和口罩刚好配套？请用含m的代数式表示．（3）在民联药店累计购医用品超过1800元后，超出1800元的部分可享受8折优惠．该校按（2）中的配套方案购买，共支付w元，求w关于m的函数关系式．若该校九年级有900名学生，需要购买口罩和水银体温计各多少盒？所需总费用为多少元？23．定义：有一组对角互余的四边形叫做对余四边形．理解：（1）若四边形是对余四边形，则与的度数之和为______；证明：（2）如图1，是的直径，点在上，，相交于点D．求证：四边形是对余四边形； 探究：（3）如图2，在对余四边形中，，，探究线段，和之间有怎样的数量关系？写出猜想，并说明理由．24．如图，在平面直角坐标系中，直线与x轴交于点A，与y轴交于点B，抛物线过点B且与直线相交于另一点．（1）求抛物线的解析式；（2）点P是抛物线上的一动点，当时，求点P的坐标；（3）点在x轴的正半轴上，点是y轴正半轴上的一动点，且满足．①求m与n之间的函数关系式；②当m在什么范围时，符合条件的N点的个数有2个？ 参考答案1．C【解析】【分析】各式计算得到结果，即可作出判断．【详解】解：A、=1，故选项不符合；B、=5，故选项不符合；C、=-6，故选项符合；D、=，故选项不符合；故选C.【点睛】此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．2．B【解析】【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值大于10时，n是正数；当原数的绝对值小于1时，n是负数．【详解】解：305000000用科学记数法表示为3.05×108，故选：B． 【点睛】此题考查了科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．3．B【解析】【分析】利用合并同类项，同底数幂的乘法和除法，幂的乘方和积的乘方运算法则计算即可.【详解】解：A、，故选项不符合；B、，故选项符合；C、，故选项不符合；D、，故选项不符合；故选B.【点睛】本题考查了合并同类项，同底数幂的乘法和除法，幂的乘方和积的乘方运算，掌握运算法则是关键.4．A【解析】【分析】根据主视图、左视图、俯视图是分别从物体正面、侧面和上面看所得到的图形，从而得出该几何体的左视图．【详解】 解：该几何体的左视图是：故选A.【点睛】本题考查了三视图，考验学生的思考能力和对几何体三种视图的空间想象能力．5．D【解析】【分析】根据折线统计图得出甲乙成绩的各项数据，从而判断各选项.【详解】解：由图可知：甲运动员的成绩为：6、7、10、8、9，乙运动员的成绩为：8、9、8、7、8，A、甲的最好成绩为10环，乙的最好成绩为9环，故选项错误；B、甲的成绩平均数为：（6+7+10+8+9）÷5=8，乙的成绩平均数为：（8+9+8+7+8）÷5=8，一样大，故选项错误；C、甲的成绩的中位数为8，乙的成绩的中位数为8，一样大，故选项错误；D、甲的成绩的方差为=2，乙的成绩的方差为=0.4， 0.4＜2，所以乙的成绩比甲稳定，故选项正确；故选D.【点睛】本题考查了平均数、中位数、方差，关键是根据甲乙的成绩计算出各项数据.6．D【解析】【分析】根据圆周角定理得出∠AOB=90°，再利用S阴影=S扇形OAB-S△OAB算出结果.【详解】解：∵∠C=45°，∴∠AOB=90°，∵OA=OB=2，∴S阴影=S扇形OAB-S△OAB==，故选D.【点睛】本题考查了圆周角定理，扇形面积计算，解题的关键是得到∠AOB=90°.7．B【解析】 【分析】根据“好点”的定义判断出“好点”即是直线y=x上的点，再各函数中令y=x，对应方程无解即不存在“好点”.【详解】解：根据“好点”的定义，好点即为直线y=x上的点，令各函数中y=x，A、x=-x，解得：x=0，即“好点”为（0，0），故选项不符合；B、，无解，即该函数图像中不存在“好点”，故选项符合；C、，解得：，经检验是原方程的解，即“好点”为（，）和（-，-），故选项不符合；D、，解得：x=0或3，即“好点”为（0，0）和（3，3），故选项不符合；故选B.【点睛】本题考查了函数图像上的点的坐标，涉及到解分式方程，一元二次方程，以及一元一次方程，解题的关键是理解“好点”的定义.8．C【解析】【分析】根据折叠的性质得到∠AEB=∠AEF，再根据点E是BC中点可得EF=EC，可得∠EFC=∠ECF，从而推出∠ECF=∠AEB，求出即可得到结果.【详解】解：由折叠可得：AB=AF=2，BE=EF，∠AEB=∠AEF，∵点E是BC中点，， ∴BE=CE=EF=，∴∠EFC=∠ECF，AE=，∵∠BEF=∠AEB+∠AEF=∠EFC+∠ECF，∴∠ECF=∠AEB，∴==，故选C.【点睛】本题考查了矩形的性质和折叠的性质，以及余弦的定义，解题的关键是利用折叠的性质得到∠ECF=∠AEB.9．-3【解析】【分析】点A在数轴上表示的数是3，根据相反数的含义和求法，判断出点A表示的数的相反数是多少即可．【详解】解：∵点A在数轴上表示的数是3，∴点A表示的数的相反数是-3．故答案为：-3．【点睛】此题主要考查了在数轴上表示数的方法，以及相反数的含义和求法，要熟练掌握．10．m（x-1）2【解析】 【分析】先提取公因式m，再利用完全平方公式进行因式分解即可．【详解】故答案为：．【点睛】本题考查了因式分解的问题，掌握完全平方公式是解题的关键．11．∠1=∠4（答案不唯一）【解析】【分析】根据平行线的判定添加条件即可.【详解】解：如图，若∠1=∠4，则a∥b，故答案为：∠1=∠4（答案不唯一）【点睛】本题考查了平行线的判定，可围绕截线找同位角、内错角和同旁内角解答.12．n≥0【解析】 【分析】根据平方的非负性可得结果．【详解】解：∵关于x的一元二次方程有实数根，而，∴n≥0，故答案为：n≥0．【点睛】本题考查了一元二次方程的解，掌握根的判别方法是解题的关键．13．【解析】【分析】先画树状图展示所有6种等可能的结果数，再找出小聪和小慧被同时选中的结果数，然后根据概率公式求解．【详解】解：画树状图如下：可知：共有6种等可能的结果，其中小聪和小慧同时被选中的情况有1种，∴小聪和小慧被同时选中的概率是， 故答案为：.【点睛】本题考查了列表法与树状图法：利用列表法或树状图展示所有等可能的结果数，再找出某事件所占有的结果数，然后根据概率公式计算这个事件的概率．14．20.8【解析】【分析】证明△ABP是等腰三角形，过P作PD⊥AB，从而求得PD的长即可．【详解】解：过P作PD⊥AB于D，∵AB=24，∵∠PAB=90°-60°=30°，∠PBD=90°-30°=60°，∴∠BPD=30°，∴∠APB=30°，即∠PAB=∠APB，∴AB=BP=24，在直角△PBD中，PD=BP•sin∠PBD=24×=≈20.8.故答案为：20.8.【点睛】 本题主要考查了解直角三角形的应用，正确作出垂线，转化为直角三角形的计算是解决本题的关键．15．bc=a【解析】【分析】根据题目中的数字，可以发现相邻的数字之间的关系，从而可以得到a，b，c之间满足的关系式．【详解】解：∵一列数：3，，，，，，，，…，可发现：第n个数等于前面两个数的商，∵a，b，c表示这列数中的连续三个数，∴bc=a，故答案为：bc=a．【点睛】本题考查数字的变化类，解答本题的关键是明确题意，发现题目中数字的变化规律，求出a，b，c之间的关系式．16．①②③【解析】【分析】证明∠BAE=∠CEG，结合∠B=∠BCD可证明△ABE∽△ECG，可判断①；在BA上截取BM=BE，证明△AME≌△ECF，可判断②；可得△AEF为等腰直角三角形，证明∠BAE+∠DAF=45°，结合∠BAE=∠CEF，∠FCH=45°=∠CFE+∠CEF，可判断③；设BE=x，则BM=x，AM=AB-BM=2-x，根据△AME≌△ECF，求出△AME面积的最大值即可判断④. 【详解】解：∵四边形ABCD为正方形，∴∠B=∠BCD=90°，∵∠AEF=90°，∴∠AEB+∠CEG=90°，又∠AEB+∠BAE=90°，∴∠BAE=∠CEG，∴△ABE∽△ECG，故①正确；在BA上截取BM=BE，∵四边形ABCD为正方形，∴∠B=90°，BA=BC，∴△BEM为等腰直角三角形，∴∠BME=45°，∴∠AME=135°，∵BA-BM=BC-BE，∴AM=CE，∵CF为正方形外角平分线，∴∠DCF=45°，∴∠ECF=135°=∠AME，∵∠BAE=∠FEC，∴△AME≌△ECF（ASA），∴AE=EF，故②正确；∴△AEF为等腰直角三角形，∴∠EAF=∠EFA=45°，∴∠BAE+∠DAF=45°，而∠BAE=∠CEF，∠FCH=45°=∠CFE+∠CEF， ∴，故③正确；设BE=x，则BM=x，AM=AB-BM=2-x，S△AME=•x•（2-x）=，当x=1时，S△AME有最大值，而△AME≌△ECF，∴S△AME=S△CEF，∴S△CEF有最大值，所以④错误；综上：正确结论的序号是：①②③.故答案为：①②③.【点睛】本题考查了全等三角形的判定和性质，相似三角形的判定，等腰直角三角形的判定和性质，正方形的性质，二次函数的最值，解题的关键是添加辅助线，灵活运用全等三角形的知识解决线段的问题.17．（1）0；（2）-3＜x＜-2【解析】【分析】（1）根据实数的混合运算法则计算即可；（2）分别解得两个不等式的解集，再合并即可.【详解】 解：（1）原式==0；（2），解不等式①得：x＜-2，解不等式②得：x＞-3，∴不等式组的解集为：-3＜x＜-2.【点睛】本题考查了实数的混合运算与解不等式组，以及特殊角的三角函数值，解题的关键是掌握运算法则.18．（1）见解析；（2）见解析【解析】【分析】（1）根据四边形ABCD为平行四边形，得出AF∥BE，由作图过程可知AF=BE，结合AB=BE即可证明；（2）利用菱形对角线互相垂直的性质，连接AE和BF，交点即为点P.【详解】解：（1）根据作图过程可知：AB=BE，AF=BE，∵四边形ABCD为平行四边形，∴AF∥BE，∵AF=BE，∴四边形ABEF为平行四边形， ∵AB=BE，∴平行四边形ABEF为菱形；（2）如图，点P即为所作图形，∵四边形ABEF为菱形，则BF⊥AE，∴∠APB=90°.【点睛】本题考查了菱形的判定和性质，平行四边形的性质，解题的关键是利用相应的性质进行画图.19．（1），；（2）8；（3）-2＜x＜0或x＞6.【解析】【分析】（1）把A代入反比例函数，根据待定系数法即可求得m，得到反比例函数的解析式，然后将代入，求得a，再根据待定系数法求得一次函数的解析式即可；（2）求出一次函数图像与x轴交点坐标，再利用面积公式计算即可；（3）根据图象得到一次函数图像在反比例函数图像上方时的x取值范围．【详解】解：（1）把代入反比例函数得：m=6，∴反比例函数的解析式为， ∵点在反比例函数图像上，∴-3a=6，解得a=-2，∴B（-2，-3），∵一次函数y1=kx+b的图象经过A和B，∴，解得：，∴一次函数的解析式为；（2）∵，，一次函数的解析式为，令y=0，解得：x=4，即一次函数图像与x轴交点为（4，0），∴S△AOB=，故答案为：8；（3）由图象可知：时，即一次函数图像在反比例函数图像上方，x的取值范围是：-2＜x＜0或x＞6.【点睛】此题是考查一次函数与反比例函数的交点问题、待定系数法求一次函数解析式，待定系数法求反比例函数解析式，待定系数法求函数解析式是中学阶段求函数解析式常用的方法，一定要熟练掌握并灵活运用．20．（1）50，20，8；（2）115.2°；（3）722【解析】【分析】 （1）根据B组人数和所占百分比求出被调查的学生总数，再根据C组所占百分比求出a值，最后根据A组人数求出所占百分比；（2）求出D组所占百分比，再乘以360°即可；（3）用样本中在线阅读时间不少于的总人数除以50，再乘以全校总人数即可.【详解】解：（1）∵B组的人数为8人，所占百分比为16%，∴被调查的同学共有8÷16%=50人，a=50×40%=20人，4÷50×100%=8%，∴m=8，故答案为：50，20，8；（2）（1-40%-16%-8%-4%）×360°=115.2°，则扇形统计图中扇形D的圆心角的度数为：115.2°；（3）950×=722人，∴全校有722学生平均每天的在线阅读时间不少于.【点睛】本题考查频数分布表、扇形统计图、用样本估计总体，解答本题的关键是明确题意，利用数形结合的思想解答．21．（1）见解析；（2）【解析】【分析】（1）连接OD，根据切线的性质得到∠BDF+∠ADO=90°，再结合∠ADO=∠OAD，推出∠BDF=∠B，即可； （2）过F作FG⊥BD于G，先利用三角函数求出BG=DG，再过点O作OH⊥AD于H，在△AOH中，求出AO即可.【详解】解：（1）连接OD，∵DF和半圆相切，∴OD⊥DF，∴∠BDF+∠ADO=90°，∵∠ADO=∠OAD，∴∠OAD+∠BDF=90°，又∠C=90°，∴∠OAD+∠B=90°，∴∠BDF=∠B，∴BF=DF；（2）过F作FG⊥BD于G，则GF垂直平分BD，∵，∴BF=DF=2，∵，，∠C=90°，∴AB=，∴cos∠B==，∴，解得：BG==DG，∴AD=AB-BD=，过点O作OH⊥AD于H， ∴AH=DH=AD=，∵cos∠BAC=，∴AO=，即半圆O的半径长为.【点睛】本题考查了切线的性质，相似三角形的判定和性质，等腰三角形的判定和性质，解直角三角形，解题的关键是正确寻找相似三角形，学会添加常用辅助线，属于中考常考题型．22．（1）每盒口罩和每盒水银体温计的价格各是200元，50元；（2）；（3），需要购买口罩18盒，水银体温计90盒，所需总费用为6840元.【解析】【分析】（1）设每盒水银体温计的价格是x元，根据用1200元购买口罩盒数与用300元购买水银体温计的盒数相同列出方程，求解即可；（2）先用m表示出需要水银体温计的支数，再表示出水银体温计的盒数；（3）分当m≤4时，当m＞4时，分别得出关系式，再合并，根据若该校九年级有900名学生求出口罩的盒数m，从而得到体温计的盒数以及总费用.【详解】 解：（1）设每盒水银体温计的价格是x元，则每盒口罩的价格是x+150元，根据题意可得：，解得：x=50，经检验：x=50是原方程的解，50+150=200元，∴每盒口罩和每盒水银体温计的价格各是200元，50元；（2）∵购买口罩m盒，∴共有口罩100m个，∵给每位学生发放2只口罩和1支水银体温计，∴需要发放支水银体温计，∴需要购买盒水银体温计；（3）由题意可得：令200m+5m×50=1800，解得：m=4，若未超过1800元，即当m≤4时，则w=200m+5m×50=450m，若超过1800元，即当m＞4时，w=（200m+5m×50-1800）×0.8+1800=360m+360，∴w关于m的函数关系式为，若该校九年级有900名学生，即=900， 解得：m=18，则=6840，答：需要购买口罩18盒，水银体温计90盒，所需总费用为6840元.【点睛】本题考查了分式方程的实际应用，一次函数的实际应用，解题的关键是理解题意，弄清口罩盒数与体温计盒数的配套关系.23．（1）90°或270°；（2）见解析；（3），理由见解析【解析】【分析】（1）分当∠A和∠C互余时，当∠B和∠D互余时，两种情况求解；（2）连接BO，得到∠BON+∠BOM=180°，再利用圆周角定理证明∠C+∠A=90°即可；（3）作△ABD的外接圆O，分别延长AC，BC，DC，交圆O于E，F，G，连接DF，DE，EF，先证明GF是圆O的直径，得到，再证明△ABC∽△FEC，△ACD∽△GCE，△BCD∽△GCF，可得，，从而得出，根据△ABC为等边三角形可得AB=AC=BC，从而得到.【详解】解：（1）∵四边形是对余四边形，当∠A和∠C互余时，∠A+∠C=90°，当∠B与∠D互余时，∠B+∠D=90°， 则∠A+∠C=360°-90°=270°，故答案为：90°或270°；（2）如图，连接BO，可得：∠BON=2∠C，∠BOM=2∠A，而∠BON+∠BOM=180°，∴2∠C+2∠A=180°，∴∠C+∠A=90°，∴四边形是对余四边形；（3）∵四边形ABCD为对于四边形，∠ABC=60°，∴∠ADC=30°，如图，作△ABD的外接圆O，分别延长AC，BC，DC，交圆O于E，F，G，连接DF，DE，EF，则∠AEF=∠ABC=60°，∠AEG=∠ADG=30°，∴∠AEF+∠AEG=90°，即∠FEG=90°，∴GF是圆O的直径，∵AB=BC，∴△ABC为等边三角形，∵∠ABC=∠AEF，∠ACB=∠ECF， ∴△ABC∽△FEC，得：，则，同理，△ACD∽△GCE，得：，则，△BCD∽△GCF，得：，可得：，而，∴，∴，∴，∵AB=BC=AC，∴.【点睛】本题考查了相似三角形的判定和性质，四边形的新定义问题，圆周角定理，等边三角形的判定和性质，多边形内角和，解题的关键是理解对余四边形的概念，结合所学知识求证. 24．（1）；（2）或（3，）或（-2，-3）；（3）①；②0＜m＜【解析】【分析】（1）利用一次函数求出A和B的坐标，结合点C坐标，求出二次函数表达式；（2）当点P在x轴上方时，点P与点C重合，当点P在x轴下方时，AP与y轴交于点Q，求出AQ表达式，联立二次函数，可得交点坐标，即为点P；（3）①过点C作CD⊥x轴于点D，证明△MNO∽△NCD，可得，整理可得结果；②作以MC为直径的圆E，根据圆E与线段OD的交点个数来判断M的位置，即可得到m的取值范围.【详解】解：（1）∵直线与x轴交于点A，与y轴交于点B，令x=0，则y=2，令y=0，则x=4，∴A（4，0），B（0，2），∵抛物线经过B（0，2），，∴，解得：，∴抛物线的表达式为：；（2）当点P在x轴上方时，点P与点C重合，满足， ∵，∴，当点P在x轴下方时，如图，AP与y轴交于点Q，∵，∴B，Q关于x轴对称，∴Q（0，-2），又A（4，0），设直线AQ的表达式为y=px+q，代入，，解得：，∴直线AQ的表达式为：，联立得：，解得：x=3或-2，∴点P的坐标为（3，）或（-2，-3），综上，当时，点P的坐标为：或（3，）或（-2，-3）； （3）①如图，∠MNC=90°，过点C作CD⊥x轴于点D，∴∠MNO+∠CND=90°，∵∠OMN+∠MNO=90°，∴∠CND=∠OMN,又∠MON=∠CDN=90°，∴△MNO∽△NCD，∴，即，整理得：；②如图，∵∠MNC=90°，以MC为直径画圆E，∵，∴点N在线段OD上（不含O和D），即圆E与线段OD有两个交点（不含O和D），∵点M在y轴正半轴，当圆E与线段OD相切时，有NE=MC，即NE2=MC2，∵M（0，m），， ∴E（，），∴=，解得：m=，当点M与点O重合时，如图，此时圆E与线段OD（不含O和D）有一个交点，∴当0＜m＜时，圆E与线段OD有两个交点，故m的取值范围是：0＜m＜.【点睛】本题是二次函数综合，考查了求二次函数表达式，相似三角形的判定和性质，圆周角定理，一次函数表达式，难度较大，解题时要充分理解题意，结合图像解决问题.