九年级中考模拟考试数学试题+锐角三角函数与特殊角附标准答案等精品复习资料大全 68页

九年级中考模拟考试数学试题+锐角三角函数与特殊角附标准答案等精品复习资料大全中考模拟考试（一）数学试卷一.选择题（每小题4分，共48分）1．四个实数0、、﹣3.14、－2中，最小的数是（　　）A．0B．C．﹣3.14D．－22．如图所示的几何体的左视图是()3.下列计算正确的是（）A．a＋a＝a2B．a3÷a＝a2C．(a－1)2＝a2－1D．(2a)3＝6a34.如图，在△ABC中，DE是AC的垂直平分线，且分别交BC，AC于点D和E，∠B＝60°，∠C＝25°，则∠BAD为（　　）A．50°B．70°C．75°D．80°5.下列说法正确的是（　　）A．了解某班学生的身高情况，适宜采用抽样调查B．数据3，5，4，1，1的中位数是4C．数据5，3，5，4，1，1的众数是1和5D．甲、乙两人射中环数的方差分别为s甲2＝2，s乙2＝3，说明乙的射击成绩比甲稳定6.已知x1、x2是关于x的方程x2﹣ax﹣2＝0的两根，下列结论一定正确的是（　　）A．x1≠x2B．x1＋x2＞0C．x1•x2＞0D．x1＜0，x2＜07.把一些书分给几名同学，若________；若每人分11本，则不够．依题意，设有x名同学可列不等式9x＋7＜11x，则横线的信息可以是（　　）A．每人分7本，则可多分9个人B．每人分7本，则剩余9本C．每人分9本，则剩余7本D．其中一个人分7本，则其他同学每人可分9本8.已知直线y＝ax＋b（a≠0）经过第一、二、四象限，则直线y＝bx－a一定不经过（） 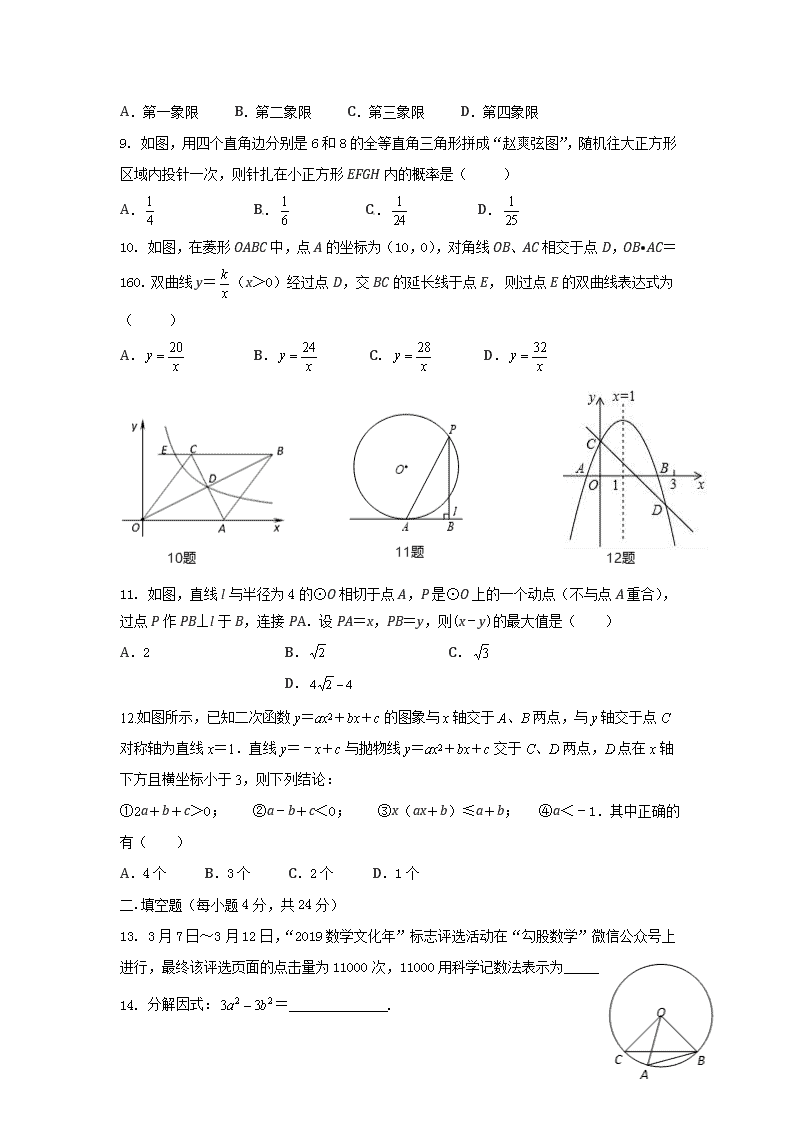A．第一象限B．第二象限C．第三象限D．第四象限9.如图，用四个直角边分别是6和8的全等直角三角形拼成“赵爽弦图”，随机往大正方形区域内投针一次，则针扎在小正方形EFGH内的概率是（）A．B．C．D．10.如图，在菱形OABC中，点A的坐标为（10，0），对角线OB、AC相交于点D，OB•AC＝160.双曲线y＝（x＞0）经过点D，交BC的延长线于点E，则过点E的双曲线表达式为（）A．B．C．D．11.如图，直线l与半径为4的⊙O相切于点A，P是⊙O上的一个动点（不与点A重合），过点P作PB⊥l于B，连接PA．设PA＝x，PB＝y，则(x﹣y)的最大值是（）A．2B．C．D．12.如图所示，已知二次函数y＝ax2＋bx＋c的图象与x轴交于A、B两点，与y轴交于点C对称轴为直线x＝1．直线y＝﹣x＋c与抛物线y＝ax2＋bx＋c交于C、D两点，D点在x轴下方且横坐标小于3，则下列结论：①2a＋b＋c＞0；②a﹣b＋c＜0；③x（ax＋b）≤a＋b；④a＜﹣1．其中正确的有（　　）A．4个B．3个C．2个D．1个二.填空题（每小题4分，共24分）13.3月7日～3月12日，“2019数学文化年”标志评选活动在“勾股数学”微信公众号上进行，最终该评选页面的点击量为11000次，11000用科学记数法表示为____________.14.分解因式：＝. 15.计算的结果为.16．如图，点B、C在⊙O上，OC⊥OB，点A在劣弧上，且OA＝AB，则∠ABC的度数为______.17．对于平面直角坐标系中任意两点，为M,N两点的直角距离,作:d(M,N).如: M(2,－3),N(1,4),则d(M,N)＝|2－1｜＋｜－3－4｜＝8.若P(x0.y0)是一定点，Q(x,y)是直线y＝kx＋b上的一动点，称d(P,Q)的最小值为P到直线y＝kx＋b的直角距离.则P(0,－3)到直线x＝1的直角距离为_______.18．如图，以正六边形ABCDEF的中心O为原点建立平面直角坐标系，过点A作AP1⊥OB于点P1，再过P1作P1P2⊥OC于点P2，再过P2作P2P3⊥OD于点P3，依次进行……若正六边形的边长为1，则点P2019的横坐标为__________.三.解答题（共8题，共78分）19.（8分）计算：20.（8分）求满足不等式组：的所有整数解．21.（8分）如图所示，是小聪同学在一次数学兴趣小组活动中，用直尺和圆规对Rt△ACB（∠ACB＝90°）进行了如下操作：①作边的垂直平分线交于点；②作的平分线，与相交于点；③连接，．请你根据操作，观察图形解答下列问题：（1）△的形状是　　　　； （2）若于点H，已知，，求的长．22.（8分）如图，AB是⊙O的直径，点P是BA延长线上一点，PC是⊙O的切线，切点为C，过点B作BD⊥PC交PC的延长线于点D，连接BC．求证：(1)∠PBC＝∠CBD；(2)BC2＝AB•BD23．（10分）某学校计划开设四门选修课：乐器、舞蹈、绘画、书法．为提前了解学生的选修情况，学校采取随机抽样的方法进行问卷调查（每个被调查的学生必须选择而且只能选择其中一门）．对调查结果进行了整理，绘制成如下两幅不完整的统计图，请结合图中所给信息解答下列问题：（1）本次调查的学生共有　　人，在扇形统计图中，m的值是　　；（2）将条形统计图补充完整；（3）在被调查的学生中，选修书法的有2名女同学，其余为男同学，现要从中随机抽取2名同学代表学校参加某社区组织的书法活动，请直接写出所抽取的2名同学恰好是1 名男同学和1名女同学的概率．24．（10分）如图1，点A（m，6），B（6，1）在反比例函数图象上，作直线AB，连接OA、OB．(1)求反比例函数的表达式和m的值；(2)求△AOB的面积；(3)如图2，E是线段AB上一点，作AD⊥x轴于点D，过点E作x轴的垂线，交反比例函数图象于点F，若EF＝AD，求出点E的坐标．25．（12分）已知一个矩形纸片OACB，将该纸片放置在平面直角坐标系中，点A(4，0)，点B(0，3)，点P为BC边上的动点（点P不与点B、C重合），经过点O、P折叠该纸片，得点B′和折痕OP．设BP＝t．(1)如图1，当∠BOP＝30°时，求点P的坐标；(2)如图2，经过点P再次折叠纸片，使点C落在直线PB′上，得点C′和折痕PQ，设AQ＝m，试用含有t的式子表示m；(3)在(2)的条件下，连接OQ，当OQ取得最小值时，求点Q的坐标；(4)在(2)的条件下，点C′能否落在边OA上?如果能，直接写出点P的坐标；如果不能，请说明理由. 26．（14分）如图，抛物线y＝ax2＋bx＋3与x轴交于A(－1，0)和B(3，0)两点，与y轴交于点C，点D是该抛物线的顶点，分别连接AC、CD、AD．(1)求抛物线的函数表达式以及顶点D的坐标；(2)在抛物线上取一点P（不与点C重合），并分别连接PA、PD，当△PAD的面积与△ACD的面积相等时，求点P的坐标；(3)将(1)中所求得的抛物线沿A、D所在的直线平移，平移后点A的对应点为A′，点C的对应点为C′，点D的对应点为D′，当四边形AA′C′C是菱形时，求此时平移后的抛物线的解析式．数学答案一.选择题（每小题4分，共48分）CABBCACDDDAA 二.填空题（每小题4分，共24分）13.1.1×10414.3(a＋b)(a－b)15.216．15°17.118.三.解答题（共8题，共78分）19.（8分）解：原式＝……………………………6分＝2；……………………………8分20.（8分）解：由x－3(x－2)≤8得：x≥1；………2分由x－1＜3－x得：x＜2；………4分∴不等式组的解为：－1≤x＜2………6分所有整数解为：－1，0，1.………8分21.（8分）解：（1）等腰直角三角形…………3分（2）过点D作DG⊥CA交CA的延长线于点G，∵平分，DH⊥BC，∴DG＝DH，……………………………4分∵∠ACB＝90°，∴四边形DHCG是正方形，∴CG＝CH，在Rt△ADG和Rt△BHG中，，∴Rt△ADG≌Rt△BHG（HL）……………………………6分∴AG＝BH，∴BC－AC＝(CH＋BH)－(CG＋AG)＝2BH∴BH＝…………………8分 22.（8分）证明：（1）连接OC．∵PC与⊙O相切，∴OC⊥PC，即∠OCP＝90°．∵BD⊥PD，∴∠BDP＝90°．∴OC∥BD．∴∠BCO＝∠CBD．∵OB＝OC，∴∠PBC＝∠BCO，∴∠PBC＝∠CBD；………4分（2）连接AC．∵AB为⊙O的直径，∴∠ACB＝90°．∴∠ACB＝∠CDB＝90°．∵∠ABC＝∠CBD，∴△ABC∽△CBD．∴＝．∴BC2＝AB•BD．………8分23.（10分）解：（1）50，30%．…………2分（2）50×20%＝10（人）50×10%＝5（人）.................4分 ．………………6分（3）∵5﹣2＝3（名），∴选修书法的5名同学中，有3名男同学，2名女同学，男男男女女男/（男，男）（男，男）（男，女）（男，女）男（男，男）/（男，男）（男，女）（男，女）男（男，男）（男，男）/（男，女）（男，女）女（女，男）（女，男）（女，男）/（女，女）女（女，男）（女，男）（女，男）（女，女）/所有等可能的情况有20种，所抽取的2名同学恰好是1名男同学和1名女同学的情况有12种，……8分则P（一男一女）＝＝答：所抽取的2名同学恰好是1名男同学和1名女同学的概率是．…………………10分24.（10分）解：（1）设反比例函数的解析式为y＝，将B(6，1)的坐标代入y＝，得k＝6．∴反比例函数的解析式为y＝．将A(m，6)的坐标代入y＝，得m＝1．……3分（2）设直线AB的解析式为y＝ax＋b，把A(1，6)和B(6，1)代入上式，得 ．解得：．∴直线AB的解析式为y＝－x＋7．……4分∴M(0，7)，N(7，0)，∴S△AOB＝S△MON－S△AOM－S△BOV＝OM×ON－OM×│xA│－ON×│yB│＝×7×7－×7×1－×7×1＝．……6分（3）设E点的坐标为（m，－m＋7），则F（m，），……7分∴EF＝－m＋7－．∵EF＝AD，∴－m＋7－＝×6．……8分解得m1＝2，m2＝3，经检验，m1＝2，m2＝3是分式方程的根，……9分∴E的坐标为（2，5）或（3，4）．……10分25.（12分）解：（1）∵A(4，0)，B(0，3)，∴OA＝4，OB＝3．在Rt△OBP中，∵∠BOP＝30°，∴PB＝＝＝．∴点的坐标为(，3)．………2分（2）由题意，得BP＝t，PC＝4－t，CQ＝3－m．由折叠可知：∠OPB＝∠OPB′，∠CPQ＝∠C′PQ．又∵∠OPB＋∠OPB′＋∠CPQ＋∠C′PQ＝180°，∴∠OPB＋∠CPQ＝90°．又∵∠OPB＋∠BOP＝90°，∴∠OPB＝∠CPQ．又∵∠OBP＝∠C＝90°，∴△OBP∽△PCQ． ∴＝．∴＝．∴m＝t2－t＋3．………7分（3）∵OQ2＝OA2＋AQ2＝42＋AQ2＝16＋AQ2，∴当AQ最短时，OQ最短．∵AQ＝m＝t2－t＋3＝(t－2)2＋，∴当t＝2时，AQ最短，OQ最短．此时点Q(4，)．………9分（4）点C′不能落在边OA上．………10分理由：假设点C′能落在边OA上．由折叠可得PB＝PB′＝t，PC＝PC′＝4－t，OB＝OB′＝3，∠OPB＝∠OPC′，∠OB′P＝∠OBP＝90°．∵BC∥OA，∴∠BPO＝∠POC′．∴∠OPC′＝∠POC′．∴OC′＝PC′＝4－t．∴B′C′＝PC－PB′＝(4－t)－t＝4－2t．在Rt△OB′C′中，∵B′O2＋B′C′2＝OC′2，∴32＋(4－2t)2＝(4－t)2．整理，得3t2－8t＋9＝0．∵△＝(－8)2－4×3×9＜0，∴该方程无实数解．∴点C′不能落在边OA上．………12分26.（14分）解：（1）设抛物线的函数表达式为y＝a(x＋1)(x－3)，则－3a＝3．∴a＝－1．∴抛物线的函数表达式为y＝－(x＋1)(x－3)， （即y＝－x2＋2x＋3）将x＝＝1代入上式，得y＝－(1＋1)(1－3)＝4．∴顶点D的坐标为(1，4)．……3分（2）将x＝0代入y＝－x2＋2x＋3，得y＝3．∴C(0，3)，OC＝3．设直线AD的解析式为y＝kx＋m,则．解得．∴直线AD的解析式为y＝2x＋2．……4分设线段AD交y轴于点E,则E(0，2)．∴CE＝OC－OE＝3－2＝1．过点C作直线l1∥AD，则直线l1的解析式为y＝2x＋3．……6分由－x2＋2x＋3＝2x＋3，解得x1＝x2＝0．将x＝0代入y＝2x＋3，得y＝3．∴直线l1与抛物线只有一个交点C．∴在线段AD上方的抛物线上不存在使△PAD的面积与△ACD的面积相等的点P．……7分将直线AD沿竖直方向向下平移1个单位长度，所得的直线l2的解析式为y＝2x＋1．直线l2与抛物线交于点P，则此时△PAD的面积与△ACD的面积相等．由－x2＋2x＋3＝2x＋1，解得x1＝，x2＝－．∴y1＝2＋1，y2＝－2＋1．∴点P的坐标为(，2＋1)或(－，－2＋1)．……9分（3）设A′的坐标为(t，2t＋2)，则A′A2＝(t＋1)2＋(2t＋2)2＝5(t＋1)2．AC2＝12＋32＝10．∵四边形AA′C′C是菱形，∴AC＝AA′．∴5(t＋1)2＝10．解得t1＝－1，t2＝－－1．∴A′的坐标为(－1，2)或(－－1，－2)．……12分①当A′在x轴上方时，A′的坐标为(－1，2)．将点A先向右平移个单位长度，再向上平移2个单位长度就得到点A′，∴将点D(1，4)先向右平移个单位长度，再向上平移2个单位长度就得到点D′(＋ 1，2＋4)．∴平移后的抛物线为y＝－(x－－1)2＋4＋2．……13分②当A′在x轴下方时，同理可得：平移后的抛物线为y＝－(x－＋1)2＋4－2．………14分一、选择题1.分析：根据互余两角的三角函数关系进行解答．解：∵∠C=90°，∴∠A+∠B=90°，∴cosB=sinA，∵sinA=，∴cosB=．故选B．点评：本题考查了互余两角的三角函数关系，熟记关系式是解题的关键．2.考点：圆周角定理；解直角三角形分析：由以△ABC的边AB为直径的半圆O，点C恰好在半圆上，过C作CD⊥AB交AB于D．易得∠ACD=∠B，又由cos∠ACD=，BC=4，即可求得答案．解答：解：∵AB为直径，∴∠ACB=90°，∴∠ACD+∠BCD=90°，∵CD⊥AB，∴∠BCD+∠B=90°，∴∠B=∠ACD，∵cos∠ACD=∴cos∠B=，∴tan∠B=，∵BC=4，∴tan∠B===，∴AC=．故选D．3考点：特殊角的三角函数值．分析：根据特殊角的三角函数值解题即可．解答：解：cos60°=．故选A． 4．考点：圆周角定理；勾股定理；锐角三角函数的定义分析：首先过点A作AD⊥OB于点D，由在Rt△AOD中，∠AOB=45°，可求得AD与OD的长，继而可得BD的长，然后由勾股定理求得AB的长，继而可求得sinC的值．解答：解：过点A作AD⊥OB于点D，∵在Rt△AOD中，∠AOB=45°，∴OD=AD=OA•cos45°=×1=，∴BD=OB﹣OD=1﹣，∴AB==，∵AC是⊙O的直径，∴∠ABC=90°，AC=2，∴sinC=．故选B．5．分析：根据锐角三角函数定义得出tanA=，代入求出即可．解：∵tanA==，AC=4，∴BC=2，故选A．67.考点：解直角三角形分析：根据三角函数的定义来解决，由sinA==，得到BC==．解答：解：∵∠C=90°AB=10，∴sinA=，∴BC=AB×=10×=6． 故选A．点评：本题考查了解直角三角形和勾股定理的应用，注意：在Rt△ACB中，∠C=90°，则sinA=，cosA=，tanA=．8.（（第1题图）考点：含30度角的直角三角形；等腰三角形的性质分析：过P作PD⊥OB，交OB于点D，在直角三角形POD中，利用锐角三角函数定义求出OD的长，再由PM=PN，利用三线合一得到D为MN中点，根据MN求出MD的长，由OD﹣MD即可求出OM的长．解答：解：过P作PD⊥OB，交OB于点D，在Rt△OPD中，cos60°==，OP=12，∴OD=6，∵PM=PN，PD⊥MN，MN=2，∴MD=ND=MN=1，∴OM=OD﹣MD=6﹣1=5．故选C．点评：此题考查了含30度直角三角形的性质，等腰三角形的性质，熟练掌握直角三角形的性质是解本题的关键．二.填空题1.考点：锐角三角函数的定义；三角形的面积；勾股定理．分析：根据正弦是角的对边比斜边，可得答案．解答：解：如图，作AD⊥BC于D，CE⊥AB于E，由勾股定理得AB=AC=2，BC=2，AD=3， 由BC•AD=AB•CE，即CE==，inA===，故答案为：．点评：本题考查锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．2.考点：切线的性质；等边三角形的判定与性质；特殊角的三角函数值．专题：计算题．解答：解：连结OM，OM的反向延长线交EF与C，如图，∵直线MN与⊙O相切于点M，∴OM⊥MF，∵EF∥MN，∴MC⊥EF，∴CE=CF，∴ME=MF，而ME=EF，∴ME=EF=MF，∴△MEF为等边三角形，∴∠E=60°，∴cos∠E=cos60°=．故答案为．3．考点：锐角三角函数的定义．分析：根据锐角三角函数的定义（tanA=）求出即可．解答：解：tanA==，故答案为：．点评：本题考查了锐角三角函数定义的应用，注意：在Rt△ACB中，∠C=90°，sinA= ，cosA=，tanA=．4.考点：解直角三角形的应用-仰角俯角问题．分析：作出图形，可得AB=500米，∠A=20°，在Rt△ABC中，利用三角函数即可求得BC的长度．解答：解：在Rt△ABC中，AB=500米，∠BAC=20°，∵=tan20°，∴BC=ACtan20°=500×0.3640=182（米）．故答案为：182．三.解答题1.考点：相似形综合题；二次函数的最值；等边三角形的性质；圆周角定理；解直角三角形解答：解：（1）∵DF⊥AB，EF⊥AC，∴∠BDF=∠CEF=90°．∵△ABC为等边三角形，∴∠B=∠C=60°．∵∠BDF=∠CEF，∠B=∠C，∴△BDF∽△CEF．（2）∵∠BDF=90°，∠B=60°，∴sin60°==，cos60°==．∵BF=m，∴DF=m，BD=．∵AB=4，∴AD=4﹣．∴S△ADF=AD•DF=×（4﹣）×m=﹣m2+m．同理：S△AEF=AE•EF=×（4﹣）×（4﹣m）=﹣m2+2．∴S=S△ADF+S△AEF=﹣m2+m+2=﹣（m2﹣4m﹣8）=﹣（m﹣2）2+3．其中0＜m＜4．∵﹣＜0，0＜2＜4，∴当m=2时，S取最大值，最大值为3．∴S与m之间的函数关系为：S═﹣（m﹣2）2+3（其中0＜m＜4）．当m=2时，S取到最大值，最大值为3． （3）如图2，∵A、D、F、E四点共圆，∴∠EDF=∠EAF．∵∠ADF=∠AEF=90°，∴AF是此圆的直径．∵tan∠EDF=，∴tan∠EAF=．∴=．∵∠C=60°，∴=tan60°=．设EC=x，则EF=x，EA=2x．∵AC=a，∴2x+x=A．∴x=．∴EF=，AE=．∵∠AEF=90°，∴AF==．∴此圆直径长为．2.考点：解直角三角形的应用．分析：设AD=x米，则AC=（x+82）米．在Rt△ABC中，根据三角函数得到AB=2.5（x+82），在Rt△ABD中，根据三角函数得到AB=4x，依此得到关于x的方程，进一步即可求解．解答：解：设AD=x米，则AC=（x+82）米．在Rt△ABC中，tan∠BCA=，∴AB=AC•tan∠BCA=2.5（x+82）．在Rt△ABD中，tan∠BDA=，∴AB=AD•tan∠BDA=4x．∴2.5（x+82）=4x，解得x=．∴AB=4x=4×≈546.7．答：AB的长约为546.7米．3.（2014•株洲，第17题，4分）计算：+（π﹣3）0﹣tan45°．解答：解：原式=4+1﹣1=4．点评：此题考查了实数的运算，熟练掌握运算法则是解本题的关键． 4.考点：解直角三角形的应用分析：设梯子的长为xm．在Rt△ABO中，根据三角函数得到OB，在Rt△CDO中，根据三角函数得到OD，再根据BD=OD﹣OB，得到关于x的方程，解方程即可求解．矚慫润厲钐瘗睞枥庑赖。解答：设梯子的长为xm．在Rt△ABO中，cos∠ABO=，∴OB=AB•cos∠ABO=x•cos60°=x．在Rt△CDO中，cos∠CDO=，∴OD=CD•cos∠CDO=x•cos51°18′≈0.625x．聞創沟燴鐺險爱氇谴净。∵BD=OD﹣OB，∴0.625x﹣x=1，解得x=8．故梯子的长是8米．5.考点：全等三角形的判定与性质；正方形的性质；解直角三角形解答：解：根据题意画出图形，过P作PN⊥BC，交BC于点N，∵四边形ABCD为正方形，∴AD=DC=PN，在Rt△ADE中，∠DAE=30°，AD=3cm，∴tan30°=，即DE=cm，根据勾股定理得：AE==2cm，∵M为AE的中点，∴AM=AE=cm，在Rt△ADE和Rt△PNQ中，，∴Rt△ADE≌Rt△PNQ（HL），∴DE=NQ，∠DAE=∠NPQ=30°，∵PN∥DC，∴∠PFA=∠DEA=60°，∴∠PMF=90°，即PM⊥AF，在Rt△AMP中，∠MAP=30°，cos30°=，∴AP===2cm；由对称性得到AP′=DP=AD﹣AP=3﹣2=1cm，综上，AP等于1cm或2cm．故答案为：1或2． 6.（第6题图）考点：解直角三角形的应用分析：过C点作FG⊥AB于F，交DE于G．在Rt△ACF中，根据三角函数可求CF，在Rt△CDG中，根据三角函数可求CG，再根据FG=FC+CG即可求解．解答：解：过C点作FG⊥AB于F，交DE于G．∵CD与地面DE的夹角∠CDE为12°，∠ACD为80°，∴∠ACF=90°+12°﹣80°=22°，∴∠CAF=68°，在Rt△ACF中，CF=AC•sin∠CAF≈0.744m，在Rt△CDG中，CG=CD•sin∠CDE≈0.336m，∴FG=FC+CG≈1.1m．故跑步机手柄的一端A的高度约为1.1m． 点评：此题考查了解直角三角形的应用，主要是三角函数的基本概念及运算，关键是用数学知识解决实际问题．7.考点：反比例函数综合题；待定系数法求反比例函数解析式；勾股定理；矩形的判定与性质；垂径定理；直线与圆的位置关系；锐角三角函数的定义专题：压轴题；探究型．分析：（1）设反比例函数的关系式y=，然后把点P的坐标（2，1）代入即可．（2）①先求出直线y=﹣x+3与x、y轴交点坐标，然后运用勾股定理即可求出△A′BC的周长；过点C作CD⊥AB，垂足为D，运用面积法可以求出CD长，从而求出sin∠BA′C的值．②由于BC=2，sin∠BMC=，因此点M在以BC为弦，半径为m的⊙E上，因而点M应是⊙E与x轴的交点．然后对⊙E与x轴的位置关系进行讨论，只需运用矩形的判定与性质、勾股定理等知识就可求出满足要求的点M的坐标．解答：解：（1）设反比例函数的关系式y=．∵点P（2，1）在反比例函数y=的图象上，∴k=2×1=2．∴反比例函数的关系式y=．（2）①过点C作CD⊥AB，垂足为D，如图1所示．当x=0时，y=0+3=3，则点B的坐标为（0，3）．OB=3．当y=0时，0=﹣x+3，解得x=3，则点A的坐标为（3，0），OA=3．∵点A关于y轴的对称点为A′，∴OA′=OA=3．∵PC⊥y轴，点P（2，1），∴OC=1，PC=2．∴BC=2． ∵∠AOB=90°，OA′=OB=3，OC=1，∴A′B=3，A′C=．∴△A′BC的周长为3++2．∵S△ABC=BC•A′O=A′B•CD，∴BC•A′O=A′B•CD．∴2×3=3×CD．∴CD=．∵CD⊥A′B，∴sin∠BA′C===．∴△A′BC的周长为3++2，sin∠BA′C的值为．②当1＜m＜2时，作经过点B、C且半径为m的⊙E，连接CE并延长，交⊙E于点P，连接BP，过点E作EG⊥OB，垂足为G，过点E作EH⊥x轴，垂足为H，如图2①所示．∵CP是⊙E的直径，∴∠PBC=90°．∴sin∠BPC===．∵sin∠BMC=，∴∠BMC=∠BPC．∴点M在⊙E上．∵点M在x轴上∴点M是⊙E与x轴的交点．∵EG⊥BC，∴BG=GC=1．∴OG=2．∵∠EHO=∠GOH=∠OGE=90°，∴四边形OGEH是矩形．∴EH=OG=2，EG=OH．∵1＜m＜2，∴EH＞EC．∴⊙E与x轴相离．∴x轴上不存在点M，使得sin∠BMC=．②当m=2时，EH=EC．∴⊙E与x轴相切．Ⅰ．切点在x轴的正半轴上时，如图2②所示．∴点M与点H重合．∵EG⊥OG，GC=1，EC=m，∴EG==．∴OM=OH=EG=．∴点M的坐标为（，0）．Ⅱ．切点在x轴的负半轴上时，同理可得：点M的坐标为（﹣，0）．③当m＞2时，EH＜EC．∴⊙E与x轴相交．Ⅰ．交点在x轴的正半轴上时， 设交点为M、M′，连接EM，如图2③所示．∵∠EHM=90°，EM=m，EH=2，∴MH===．∵EH⊥MM′，∴MH=M′H．M′H═．∵∠EGC=90°，GC=1，EC=m，∴EG===．∴OH=EG=．∴OM=OH﹣MH=﹣，∴OM′=OH+HM′=+，∴M（﹣，0）、M′（+，0）．Ⅱ．交点在x轴的负半轴上时，同理可得：M（﹣+，0）、M′（﹣﹣，0）．综上所述：当1＜m＜2时，满足要求的点M不存在；当m=2时，满足要求的点M的坐标为（，0）和（﹣，0）；当m＞2时，满足要求的点M的坐标为（﹣，0）、（+，0）、（﹣+，0）、（﹣﹣，0）． 点评：本题考查了用待定系数法求反比例函数的关系式、勾股定理、三角函数的定义、矩形的判定与性质、直线与圆的位置关系、垂径定理等知识，考查了用面积法求三角形的高，考查了通过构造辅助圆解决问题，综合性比较强，难度系数比较大．由BC=2，sin∠BMC=联想到点M在以BC为弦，半径为m的⊙E上是解决本题的关键．8.考点：解直角三角形的应用-仰角俯角问题分析：作CE⊥AB于点E，则△BCE和△BCD都是直角三角形，即可求得CE，BE的长，然后在Rt△ACE中利用三角函数求得AE的长，进而求得AB的长，即为大树的高度．解答解：作CE⊥AB于点E，在Rt△BCE中，BE=CD=5m，CE==5m，在Rt△ACE中AE=CE•tan45°=5m，AB=BE+AE=（5+5）m．故答案为：（5+5）．点评：本题考查解直角三角形的应用﹣仰角俯角问题的应用，要求学生能借助仰角构造直角三角形并解直角三角形． 9.考点：解直角三角形的应用-方向角问题分析：过点C作CD⊥AB交AB延长线于D．先解Rt△ACD得出CD=AC=40海里，再解Rt△CBD中，得出BC=≈50，然后根据时间=路程÷速度即可求出海警船到大事故船C处所需的时间．解答：解：如图，过点C作CD⊥AB交AB延长线于D．在Rt△ACD中，∵∠ADC=90°，∠CAD=30°，AC=80海里，∴CD=AC=40海里．在Rt△CBD中，∵∠CDB=90°，∠CBD=90°﹣37°=53°，∴BC=≈=50（海里），∴海警船到大事故船C处所需的时间大约为：50÷40=（小时）．点评：本题考查了解直角三角形的应用﹣方向角问题，难度适中，作出辅助线构造直角三角形是解题的关键．第15讲线段、角、相交线与平行线考点1直线、射线、线段直线公理经过两点，有且只有①条直线.线段公理两点之间，线段最②.两点间的距离连接两点间的线段的③，叫做两点间的距离.考点2角 角的概念定义1有公共端点的两条④组成的图形叫做角.定义2一条⑤绕着它的端点从一个位置旋转到另一个位置所形成的图形叫做角.互为余角定义如果两个角的和等于⑥，则这两个角互余.性质同角(或等角)的余角⑦.互为补角定义如果两个角的和等于⑧，则这两个角互补.性质同角(或等角)的补角⑨.考点3相交线对顶角对顶角相等.垂直性质1过一点有且只有⑩条直线与已知直线垂直.性质2直线外一点与直线上各点连接的所有线段中，⑪最短.点到直线的距离直线外一点到这条直线的⑫的长度，叫做点到直线的距离.考点4角的平分线与线段的垂直平分线角的平分线线段的垂直平分线性质角的平分线上的点到角两边的距离⑬.线段垂直平分线上的点与这条线段两个端点的距离⑭.判定角的内部到角的两边距离相等的点在⑮上.与一条线段两个端点距离相等的点，在这条线段的⑯上.考点5平行线平行线的概念在同一平面内，的两条直线叫做平行线.平行公理经过直线外一点有且只有条直线与已知直线平行.平行公理的推论如果两条直线都和第三条直线平行，那么这两条直线也.平行线的判定同位角相等，两直线平行.内错角相等，两直线平行.同旁内角互补，两直线平行.平行线的性质两直线平行，同位角相等.两直线平行，内错角相等.两直线平行，同旁内角互补.平行线间的距离定义过平行线上的一点作另一条平行线的垂线，的长度叫做两条平行线间的距离.性质两条平行线间的距离处处.考点6命题命题的概念判断一件事情的句子叫做命题.命题的分类命题分为命题和命题.命题的组成命题由和两个部分组成.1.若某条直线上有n个点，则线段的总条数为 条(n为大于或等于2的整数)；在角的内部从角的顶点引n条射线，可以得到个角.2.“两点之间线段最短”、“垂线段最短”在解决最短路径问题时经常用到.命题点1角的有关计算例1(2013·福州)如图，OA⊥OB，若∠1=40°，则∠2的度数是()A.20°B.40°C.50°D.60°方法归纳：计算角度时，通常结合几何图形的有关性质来找出已知角度与所求角度中的数量关系.1.下列四个角中，最有可能与70°角互补的是()2.如图，直线AB与直线CD相交于点O，E是∠AOD内一点，已知OE⊥AB，∠BOD=45°，则∠COE的度数是()A.125°B.135°C.145°D.155°3.(2014·滨州)如图，OB是∠AOC的角平分线，OD是∠COE的角平分线.如果∠AOB=40°，∠COE=60°，则∠BOD的度数为()A.50°B.60°C.65°D.70°命题点2角平分线的性质与判定 例2(2013·湘西)如图，Rt△ABC中，∠C=90°，AD平分∠CAB，DE⊥AB于E，若AC=6，BC=8，CD=3.(1)求DE的长；(2)求△ADB的面积.【思路点拨】(1)根据角平分线上的点到角两边的距离相等，DE=CD，从而可得DE的长；(2)利用勾股定理先求AB的长，再根据面积公式计算.【解答】方法归纳：解答本题的关键是通过等量代换把要求的边转化为已知的边的长.1.(2014·巴中)如图，CF是△ABC的外角∠ACM的平分线，且CF∥AB，∠ACF=50°，则∠B的度数为()A.80°B.40°C.60°D.50°2.如图，OP平分∠AOB，PA⊥OA,PB⊥OB，垂足分别为A，B.下列结论中不一定成立的是()A.PA=PBB.PO平分∠APBC.OA=OBD.AB垂直平分OP3.(2013·泉州)如图，∠AOB=70°，QC⊥OA于C，QD⊥OB于D，若QC=QD，则∠AOQ=. 命题点3线段的垂直平分线的性质与判定例3(2013·仙桃改编)如图，在△ABC中，AB=AC，∠A=120°，BC=6cm，AB的垂直平分线交BC于点M，交AB于点E，AC的垂直平分线交BC于点N，交AC于点F，求MN的长.【思路点拨】连接MA、NA.根据垂直平分线性质得出等腰三角形△CAN和△MAB，从而说明△AMN是等边三角形，找出MN与BC的关系求出MN的长.【解答】方法归纳：解答这类题的关键是要通过作辅助线构造垂直平分线模型来沟通各边或者各角之间的关系，从而达到化繁为简，化难为易的目的.1.(2014·十堰)如图，在平行四边形ABCD中，AB=4，BC=6，AC的垂直平分线交AD于点E，则△CDE的周长是()A.7B.10C.11D.122.(2013·义乌)如图，AD⊥BC于点D，D为BC的中点，连接AB，∠ABC的平分线交AD于点O，连接OC，若∠AOC＝125°，则∠ABC＝. 3.(2014·汕尾)如图，在Rt△ABC中，∠B=90°，分别以点A、C为圆心，大于AC长为半径画弧相交于点M、N，连接MN，与AC、BC分别交于点D、E，连接AE.(1)求∠ADE(直接写出结果)；(2)当AB=3，AC=5时，求△ABE的周长.命题点4平行线的性质和判定例4(2013·重庆)如图，直线a，b，c，d，已知c⊥a,c⊥b，直线b，c，d交于一点，若∠1=50°，则∠2等于()A.60°B.50C.40°D.30°方法归纳：运用平行线的判定与性质的关键点都是“同位角、内错角、同旁内角”这三对位置角的等量关系.1.(2014·德州)如图，AD是∠EAC的平分线，AD∥BC，∠B＝30°，则∠C为()A.30°B.60°C.80°D.120° 2.(2014·孝感)如图，直线l1∥l2，l3⊥l4，∠1=44°，那么∠2的度数为()A.46°B.44°C.36°D.22°3.(2014·梅州)如图，把一块含有45°角的直角三角板两个顶点放在直尺的对边上，如果∠1=20°，则∠2的度数是()A.15°B.20°C.25°D.30°4.(2014·淄博)如图，直线a∥b,点B在直线b上，且AB⊥BC,∠1=55°，求∠2的度数.1.(2014·金华)如图，经过刨平的木板上的两个点，能弹出一条笔直的墨线，而且只能弹出一条墨线，能解释这一实际应用的数学知识是()A.两点确定一条直线B.两点之间，线段最短 C.垂线段最短D.在同一平面内，过一点有且只有一条直线与已知直线垂直2.(2014·长沙)如图，C、D是线段AB上的两点，且D是线段AC的中点，若AB=10cm,BC=4cm,则AD的长为()A.2cmB.3cmC.4cmD.6cm3.(2014·济宁)把一条弯曲的公路改成直道，可以缩短路程.用几何知识解释其道理正确的是()A.两点确定一条直线B.垂线段最短C.两点之间线段最短D.三角形两边之和大于第三边4.(2014·滨州)如图，是我们学过的用直尺画平行线的方法示意图，画图原理是()A.同位角相等，两直线平行B.内错角相等，两直线平行C.两直线平行，同位角相等D.两直线平行，内错角相等5.(2014·十堰)如图，直线m∥n，则∠α为()A.70°B.65°C.50°D.40°6.(2014·河南)如图，直线AB、CD相交于O，射线OM平分∠AOC,ON⊥OM,若∠AOM=35°，则∠CON的度数为()A.35°B.45°C.55°D.65°7.(2014·汕尾)如图，能判定EB∥AC的条件是()A.∠C=∠ABEB.∠A=∠EBDC.∠C=∠ABCD.∠A=∠ABE 8.(2014·白银)如图，将直角三角尺的直角顶点靠在直尺上，且斜边与这根直尺平行.图中与∠α互余的角共有()A.1个B.2个C.3个D.4个9.(2014·荆门)如图，AB∥ED,AG平分∠BAC,∠ECF=70°,则∠FAG的度数是()A.155°B.145°C.110°D.35°10.(2014·泰安)在△ABC和△A1B1C1中，下列四个命题：(1)若AB=A1B1，AC=A1C1,∠A=∠A1，则△ABC≌△A1B1C1；(2)若AB=A1B1，AC=A1C1,∠B=∠B1，则△ABC≌△A1B1C1；(3)若∠A=∠A1，∠C=∠C1，则△ABC∽△A1B1C1；(4)若AC∶A1C1=CB∶C1B1,∠C=∠C1，则△ABC∽△A1B1C1.其中真命题的个数为()A.4个B.3个C.2个D.1个11.(2014·广安)若∠α的补角为76°28′,则∠α=.12.(2014·广州)已知命题：“如果两个三角形全等，那么这两个三角形的面积相等.”写出它的逆命题：，该逆命题是命题(填“真”或“假”).13.(2013·长沙)如图，BD是∠ABC的平分线，P是BD上的一点，PE⊥BA于点E，PE=4cm,则点P到边BC的距离为__________cm.14.(2014·威海)直线l1∥l2，一块含45°角的直角三角板如图所示放置，∠1＝85°，则∠2＝. 15.(2014·盐城)如图，点D，E分别在AB，BC上，DE∥AC，AF∥BC，∠1＝70°，则∠2＝.16.如图，CD与BE互相垂直平分，AD⊥DB,∠BDE=70°，则∠CAD=.17.(2014·益阳)如图，EF∥BC，AC平分∠BAF，∠B=80°.求∠C的度数.18.如图，线段AB=4，点O是线段AB上一点，C、D分别是线段OA、OB的中点，小明据此很轻松地求得CD=2.他在反思过程中突发奇想：若点O运动到AB的延长线上时，原有的结论“CD=2”是否仍然成立？请帮小明画出图形并说明理由.19.(2014·泰安)把一直尺放置在一个三角形纸片上，则下列结论正确的是()A.∠1+∠6>180°B.∠2+∠5<180°C.∠3+∠4<180°D.∠3+∠7>180° 20.(2014·鄂州)如图，直线a∥b,直角三角形如图放置，∠DCB=90°，若∠1+∠B=70°，则∠2的度数为()A.20°B.40°C.30°D.25°21.(2013·绥化)如图所示，以O为端点画六条射线OA、OB、OC、OD、OE、OF后，再从射线OA上某点开始按逆时针方向依次在射线上描点并连线，若将各条射线上所描的点依次记为1、2、3、4、5、6、7、8…，那么所描的第2015个点在射线上.22.(2014·梅州)如图，在Rt△ABC中，∠B=90°，分别以A、C为圆心，大于AC长为半径画弧，两弧相交于点M、N，作直线MN，与AC交于点D，与BC交于点E，连接AE.(1)∠ADE=；(2)AECE(填“>”“<”或“=”)(3)AB=3，AC=5时，△ABE的周长是.23.(2013·宁夏模拟)平面内的两条直线有相交和平行两种位置关系.(1)如图1，若AB∥CD，点P在AB、CD外部，则有∠B=∠BOD，又因∠BOD是△POD的外角，故∠BOD=∠BPD+∠D，得∠BPD=∠B-∠ D.将点P移到AB、CD内部，如图2，以上结论是否成立？若成立，说明理由；若不成立，则∠BPD、∠B、∠D之间有何数量关系？请证明你的结论；(2)在图2中，将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q，如图3，则∠BPD、∠B、∠D、∠BQD之间有何数量关系？(不需证明)参考答案考点解读①一②短③长度④射线⑤射线⑥90°⑦相等⑧180°⑨相等⑩一⑪垂线段⑫垂线段⑬相等⑭相等⑮角的平分线⑯垂直平分线不相交一平行垂线段相等真假题设结论各个击破例1C题组训练1.D2.B3.D例2(1)在Rt△ABC中，∠C=90°，∴AC⊥CD.又∵AD平分∠CAB，DE⊥AB，∴DE=CD.又∵CD=3，∴DE=3.(2)在Rt△ABC中，∠C=90°，AC=6，BC=8，∴AB===10,∴S△ADB=AB·DE=×10×3=15.题组训练1.D2.D3.35°例3连接MA、NA.∵AB的垂直平分线交BC于M，AC的垂直平分线交BC于N，∴BM=AM，CN=AN，∴∠MAB=∠B，∠CAN=∠C.∵∠BAC=120°，AB=AC，∴∠B=∠C=30°,∴∠BAM+∠CAN=60°，∠AMN=∠ANM=60°，∴△AMN是等边三角形, ∴AM=AN=MN，∴BM=MN=NC，∴MN=BC=2cm.题组训练1.B2.70°3.(1)∠ADE=90°.(2)在Rt△ABC中，∠B=90°，AB=3，AC=5，∴BC=4.又∵MN为AC的垂直平分线，∴AE=EC.C△ABE=AB+BE+AE=AB+BE+EC=AB+BC=7.例4B题组训练1.A2.A3.C4.设直线b与BC所交的另一个锐角为∠3.∵AB⊥BC,∴∠1+∠3=90°.∵∠1=55°,∴∠3=35°.∵a∥b,∴∠2=∠3=35°.整合集训1.A2.B3.C4.A5.C6.C7.D8.B9.B10.B11.103°42′12.如果两个角形的面积相等，那么这两个三角形全等假13.414.4015.70°16.70°17.∵EF∥BC,∴∠BAF=180°-∠B=100°.∵AC平分∠BAF,∴∠CAF=∠BAF=50°.∵EF∥BC，∴∠C=∠CAF=50°.18.仍然成立，∵C，D分别是线段OA，OB的中点，∴OC=OA，OD=OB.CD=OC-OD=OA-OB=(OA-OB)=AB=2.19.D20.A21.OE22.(1)90°(2)=(3)723.(1)不成立，结论是∠BPD=∠B+∠D.证明：延长BP交CD于点E.∵AB∥CD，∴∠B=∠BED. 又∵∠BPD=∠BED+∠D，∴∠BPD=∠B+∠D.(2)结论：∠BPD=∠BQD+∠B+∠D.第8讲一元一次不等式(组)考点1不等式的概念及性质不等式的有关概念用不等号连接起来的式子叫做不等式，使不等式成立的未知数的取值范围叫做不等式的解集.不等式的基本性质性质1若a＜b，则a±c＜b±c；性质2若a＜b且c＞0，则ac①bc(或②)；性质3若a＜b且c＜0，则ac③bc(或④).考点2一元一次不等式(组)的解法一元一次不等式的解法(1)去分母；(2)去括号；(3)移项；(4)合并同类项；(5)系数化为1.不等式组的解法一般先分别求出不等式组中各个不等式的解集，并表示在数轴上，再求出他们的公共部分，就得到不等式组的解集.不等式组的解集情况(假设b＜a)x＞a同大取大x≤b同小取小b≤x＜a大小小大中间找无解大大小小无处找考点3不等式的应用列不等式解应用题和列方程解应用题的一般步骤基本相似，其步骤包括：(1)审清题意；(2)设未知数；(3)列不等式；(4)解不等式；(5)⑤作答.1.已知不等式(组)的解集确定不等式(组)中字母的取值范围有以下四种方法：(1)逆用不等式(组)解集确定；(2)分类讨论确定；(3)从反面求解确定；(4)借助数轴确定. 2.列不等式(组)解应用题应紧紧抓住“至多”、“至少”、“不大于”、“不小于”、“不超过”、“大于”、“小于”等关键词列出不等量关系式，进而求解.命题点1一元一次不等式的解法例1(2014·连云港)解不等式2(x-1)+5<3x，并把解集在数轴上表示出来.【思路点拨】先去括号，化不等式为2x-2+5<3x，再移项、合并同类项即可.【解答】方法归纳：一元一次不等式的解法步骤一般是：去分母、去括号、移项、合并同类项、系数化1，值得注意的是：去分母、系数化1时，如果两边同乘负数，不等号一定要变号；用数轴表示不等式的解集时一定要注意包含界点需用实心的小圆点，不包含界点需用空心的小圆圈.1.(2014·黔西南)不等式2x-4>0的解集为()A.x>B.x>2C.x>-2D.x>82.(2013·福州)不等式1+x＜0的解集在数轴上表示正确的是()3.(2015·齐齐哈尔模拟)解不等式2(x-1)-3＜1，并把它的解集在数轴上表示出来.命题点2一元一次不等式组的解法例2(2014·台州)解不等式组：并把解集在下面数轴上表示出来.【思路点拨 】本题考查了不等式组的解法和解集在数轴上的表示方法.先确定每一个不等式的解集，再确定不等式组的解集，进而将其解集表示在数轴上.【解答】方法归纳：解一元一次不等式组的步骤：①求出这个不等式组中各个不等式的解集；②利用数轴求出这些不等式的解集的公共部分，即求出了这个不等式组的解集.确定不等式组的解集一般有两种方法，即口诀法和数轴法.1.(2014·云南)不等式组的解集是()A.x＞B.-1≤x＜C.x＜D.x＞-12.(2014·邵阳)不等式组的解集在数轴上表示正确的是()3.(2014·聊城)不等式组的解集是.4.(2014·广安)解不等式组并写出不等式组的整数解.命题点3一元一次不等式的应用(2013·呼和浩特)某次知识竞赛共有20道题，每一题答对得10分，答错或不答都扣5分.小明得分要超过90分，他至少要答对多少道题？ 【思路点拨】设小明答对x道题，根据得失分数，列一元一次不等式，再求满足不等式的最小整数解.【解答】方法归纳：求实际问题中的“至多”、“至少”这类问题，常采用不等式锁范围，即先根据题目的问题，直接设出未知数，列出不等式，求出相应的范围，再根据题目的条件，知道它是正整数或整数等，求出答案.1.(2014·南京)铁路部门规定旅客免费携带行李箱的长、宽、高之和不超过160cm.某厂家生产符合该规定的行李箱，已知行李箱的高为30cm，长与宽的比为3∶2，则该行李箱的长的最大值为78cm.2.某公园出售的一次性使用门票，每张10元，为了吸引更多游客，新近推出购买“个人年票”的售票活动(从购买日起，可供持票者使用一年).年票分A、B两类：A类年票每张100元，持票者每次进入公园无需再购买门票；B类年票每张50元，持票者进入公园时需再购买每次2元的门票.某游客一年中进入该公园至少要超过多少次时，购买A类年票最合算？1.(2014·滨州)a、b都是实数，且ab+xB.-a+1<-b+1C.3a<3bD.>2.下列说法中，错误的是()A.不等式x<2的正整数解只有一个B.-2是不等式2x-1<0的一个解C.不等式-3x>9的解集是x>-3D.不等式x<10的整数解有无数个3.(2013·绵阳)设“▲”、“●”、“■”分别表示三种不同的物体，现用天平秤两次，情况如图所示，那么▲、●、■这三种物体按质量从大到小排列应为() A.■、●、▲B.▲、■、●C.■、▲、●D.●、▲、■4.(2013·汕头)不等式5x-1>2x+5的解集在数轴上表示正确的是()5.(2014·南充)不等式组的解集在数轴上表示正确的是()6.(2014·株洲)一元一次不等式组的解集中，整数解的个数是()A.4B.5C.6D.77.(2014·潍坊)若不等式组无解，则实数a的取值范围是()A.a≥-1B.a＜-1C.a≤1D.a≤-18.(2015·原创)篮球联赛中，每场比赛都要分出胜负，每队胜1场得2分，负1场得1分.某队预计在2014~2015赛季全部22场比赛中最少得到36分，才有希望进入季后赛.假设这个队在将要举行的比赛中胜x场，要达到目标，x应满足的关系式是()A.2x+(22-x)≥36B.2x-(22-x)≥36C.2x+(22-x)≤36D.2x≥369.(2014·温州)不等式3x-2>4的解是.10.(2013·张掖)不等式2x+9≥3(x+2)的正整数解是.11.(2013·安顺)若关于x的不等式(1-a)x>2可化为x<，则a的取值范围是. 12.(2014·江西)不等式组的解集是.13.(2013·烟台)不等式组的最小整数解是.14.有3人携带会议材料乘坐电梯，这3人的体重共210kg，每捆材料重20kg，电梯最大负荷为1050kg，则该电梯在此3人乘坐的情况下最多还能搭载捆材料.15.(2013·巴中)解不等式-≤1，并把解集表示在数轴上.16.(2014·菏泽)解不等式组并判断x＝是否为该不等式组的解.17.(2013·毕节)解不等式组将不等式组的解集在数轴上表示出来，并写出不等式组的非负整数解.18.(2014·邵阳)小武新家装修，在装修客厅时，购进彩色地砖和单色地砖共100块，共花费5600元.已知彩色地砖的单价是80元/块，单色地砖的单价是40元/块.(1)两种型号的地砖各采购了多少块？(2)如果厨房也铺设这两种型号的地砖共60块，且采购地砖的费用不超过3200元，那么彩色地砖最多能采购多少块？ 19.(2013·荆州)在实数范围内规定新运算“△”，其规则是：a△b=2a-b.已知不等式x△k≥1的解集在数轴上如图表示，则k的值是.20.若关于x、y的二元一次方程组的解满足x+y＞1，则k的取值范围是.21.(2014·呼和浩特)已知实数a是不等于3的常数，解不等式组并依据a的取值情况写出其解集.22.（2014·绥化）某商场用36万元购进A、B两种商品，销售完后共获利6万元，其进价和售价如下表：AB进价（元/件）12001000售价（元/件）13801200（1）该商场购进A、B两种商品各多少件？（2）商场第二次以原进价购进A、B两种商品．购进B种商品的件数不变，而购进A种商品的件数是第一次的2倍，A种商品按原售价出售，而B种商品打折销售．若两种商品销售完毕，要使第二次经营活动获利不少于81600元，B种商品最低售价为每件多少元？参考答案考点解读①＜②＜③＞④＞⑤检验各个击破例1去括号，得2x-2+5<3x， 移项，得2x-3x<2-5，合并，得-x<-3，系数化为1，得x>3.不等式的解集在数轴上表示为：题组训练1.B2.A3.去括号，得2x-2-3＜1，移项，得2x＜2+3+1，合并同类项，得2x＜6，系数化为1，得x＜3.不等式的解集在数轴上表示如图：例2解不等式①，得x＞2，解不等式②，得x＜3，∴原不等式组的解集是2＜x＜3.解集表示在数轴上如图.题组训练1.A2.B3.-90.解得x>12.∵x为整数，∴x最小为13.答：他至少要答对13道题.题组训练1.782.设某游客一年中进入该公园x次，由题意，得100＜50+2x.解得x＞25.答：游客一年中进入该公园至少要超过25次时，购买A类年票最合算.整合集训1.C2.C3.C4.A5.D6.C7.D8.A9.x>210.1，2，311.a＞112.x＞13.314.4215.去分母，得2(2x-1)-(9x+2)≤6，去括号，得4x-2-9x-2≤6， 移项，得4x-9x≤6+2+2，合并同类项，得-5x≤10，系数化为1，得x≥-2.解集在数轴上表示为：16.由①得x＞-3.由②得x≤1.∴原不等式组的解集是-3＜x≤1.∵＞1，∴x＝不是该不等式组的解.17.解不等式①，得x≥-1.解不等式②，得x＜3.所以原不等式组的解集是-1≤x＜3.其解集在数轴上表示为：所以不等式组的非负整数解有：0，1，2.18.(1)设彩色地砖采购x块，则单色地砖采购(100-x)块.根据题意，得80x+40(100-x)＝5600.解得x＝40.100-x＝60.答：彩色地砖采购40块，单色地砖采购60块.(2)设彩色地砖采购y块，则单色地砖采购(60-y)块，则80y+40(60-y)≤3200.解得y≤20.答：彩色地砖最多能采购20块.19.-320.k>221.解①得x≤3，解②得x3时，不等式组的解集为x≤3；当a<3时，不等式组的解集为x