中考数学复习冲刺专项训练精讲：尺规作图教学课件 12页

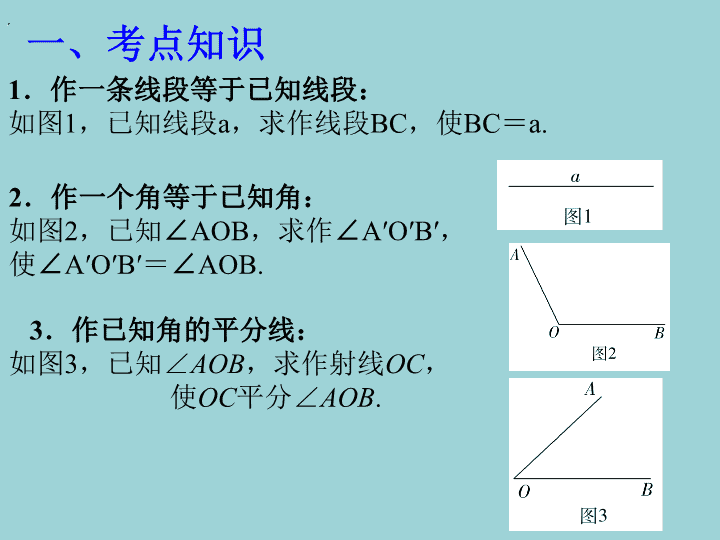
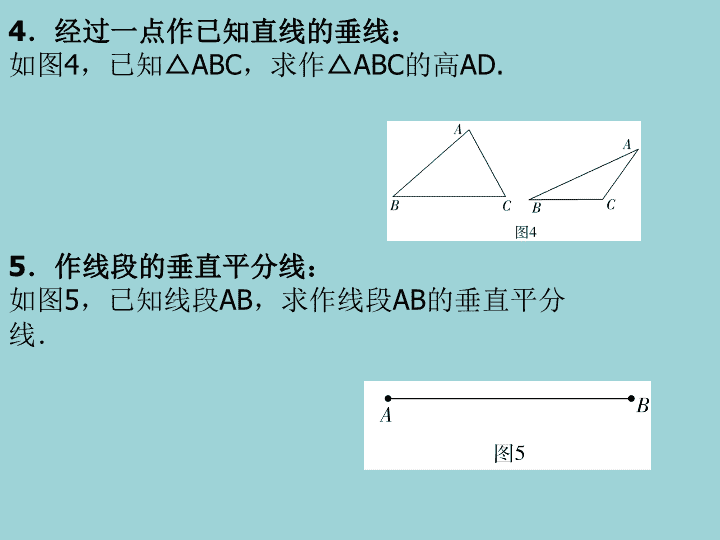
第四章三角形尺规作图中考数学复习冲刺专项训练精讲 1．作一条线段等于已知线段：如图1，已知线段a，求作线段BC，使BC＝a.一、考点知识，2．作一个角等于已知角：如图2，已知∠AOB，求作∠A′O′B′，使∠A′O′B′＝∠AOB.3．作已知角的平分线：如图3，已知∠AOB，求作射线OC，使OC平分∠AOB. 4．经过一点作已知直线的垂线：如图4，已知△ABC，求作△ABC的高AD.5．作线段的垂直平分线：如图5，已知线段AB，求作线段AB的垂直平分线． 【例1】已知线段a，b如图所示，求作直角三角形ABC，使得斜边AB＝a，一条直角边BC＝b.(保留作图痕迹，不写作法)【考点1】作一条线段等于已知线段，经过一点作已知直线的垂线二、例题与变式解：作图略【变式1】如图，已知线段a，c，∠α.求作：△ABC，使BC＝a，AB＝c，∠ABC＝∠α.解：作图略 【考点2】作已知角的平分线【例2】如图，等腰三角形ABC的顶角∠A＝36°.(1)作底角∠ABC的平分线BD，交AC于点D(用尺规作图，不写作法，但保留作图痕迹)；(2)通过计算说明△ABD和△BDC都是等腰三角形．解：（1）作图略（2）∵∠A=36°，∴∠ABC=∠C=(180°－36°)÷2=72°.∵BD平分∠ABC，∴∠ABD=∠DBC=72°÷2=36°.∴∠CDB=180°－36°－72°=72°.∵∠A=∠ABD=36°，∠C=∠CDB=72°，∴AD=DB，BD=BC.∴△ABD和△BDC都是等腰三角形. 【变式2】如图，点D在△ABC的边AB上，且∠ACD＝∠A.(1)作∠BDC的平分线DE，交BC于点E(用尺规作图，保留作图痕迹，不写作法)；(2)在(1)的条件下，判断直线DE与直线AC的位置关系，并证明．解：（1）作图略（2）DE∥AC，∵DE平分∠BDC，∴∠BDE=∠BDC，∵∠ACD=∠A，∠ACD+∠A=∠BDC，∴∠A=∠BDC，∴∠A=∠BDE.∴DE∥AC. 【考点3】作线段的垂直平分线【例3】如图，在Rt△ABC中，∠ACB＝90°.(1)用尺规在边BC上求作一点P，使PA＝PB(不写作法，保留作图痕迹)；(2)连接AP，当∠B为__________时，AP平分∠CAB.并说明理由．解：（1）作图略（2）∠B=30°，理由如下：∵PA=PB，∴∠B=∠BAP.又∵AP平分∠CAB，∴∠CAP=∠BAP=∠B.∵在Rt△ABC中，∠ACB=90°,∴∠CAP=∠BAP=∠B=30°,即∠B=30°. 【变式3】如图，BD是矩形ABCD的一条对角线．(1)作BD的垂直平分线EF，分别交AD，BC于点E，F，垂足为点O.(要求用尺规作图，保留作图痕迹，不要求写作法)；(2)求证：DE＝BF.解：（1）作图略（2）∵四边形ABCD为矩形，∴AD∥BC，∴∠ADB=∠CBD，∵EF垂直平分线段BD，∴BO=DO.在△DEO和△BFO中，∠ADB＝∠CBD，BO＝DO，∠DOE＝∠BOF，∴△DEO≌△BFO（ASA）.∴DE=BF． A组1．如图，已知在△ABC中，按以下步骤作图：(1)分别以B，C为圆心，大于BC的长为半径作弧，两弧相交于两点M，N；(2)作直线MN交AB于点D，连接CD.若CD＝AC，∠A＝50°，则∠ACB＝______．三、过关训练2．如图，在Rt△ABC中，∠ACB＝90°，AC＝6,BC＝8.(1)分别以点A，B为圆心，大于AB的长为半径作弧，两弧相交于点E，F，作直线EF交AB于点D；(用尺规作图，不写作法，但保留作图痕迹)(2)连接CD，求CD的长．105°解：（1）图略（2）由（1）可得直线EF垂直平分AB，且D是AB的中点，又∵∠ACB=90°，∴CD=AB，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，∴.∴CD=AB=5. 3．如图，△ABC中，∠BAC＝90°，AD⊥BC，垂足为D.(1)求作∠ABC的平分线，分别交AD，AC于P，Q两点；(尺规作图，保留作图痕迹，不写作法)(2)求证：AP＝AQ.解：（1）作图略（2）∵AD⊥BC，∴∠ADB=90°.∴∠BPD+∠PBD=90°.∵∠BAC=90°，∴∠AQP+∠ABQ=90°.又∵BQ平分∠ABC，∴∠BPD=∠AQP.∵∠BPD=∠APQ，∴∠APQ=∠AQP.∴AP=AQ. 4．如图，在△ABC中，∠ACB＝90°，∠A＝30°，BC＝4.(1)过点C作AB边的垂线，垂足为D；(尺规作图，保留作图痕迹，不写作法)(2)求AD的长．解：（1）图略（2）在△ABC中，∠ACB=90°，∠A=30°，BC=4，∴AB=2BC=8，∠B=60°.由（1）可得CD⊥AB，∴∠BCD=30°.∴BD=BC=2.∴AD=AB－BD=6. B组5．如图，△ABC是直角三角形，∠ACB＝90°，作∠BAC的平分线，交BC于点O，再以O为圆心，OC为半径作圆．(尺规作图，不写作法，但保留作图痕迹)(1)AB与⊙O的位置关系是__________；(直接写出答案)(2)若AC＝5，BC＝12，求⊙O的半径．解：（1）AB与⊙O相切.（2）设AB与⊙O相切于点D，由∠B=∠B，∠BDO=∠ACB=90°，得△BOD∽△BAC.∴.设半径OD=x，，解得x=.∴⊙O的半径为.