安徽省2021年中考数学模拟试题含答案（3） 13页

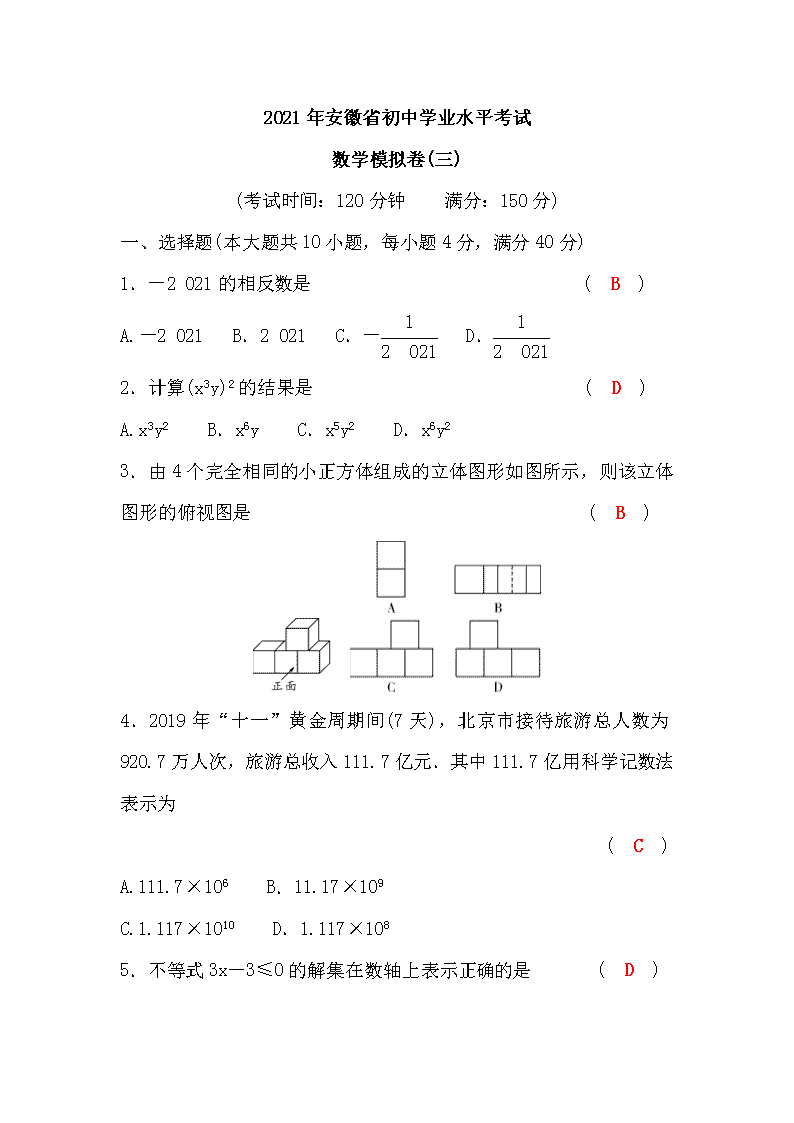
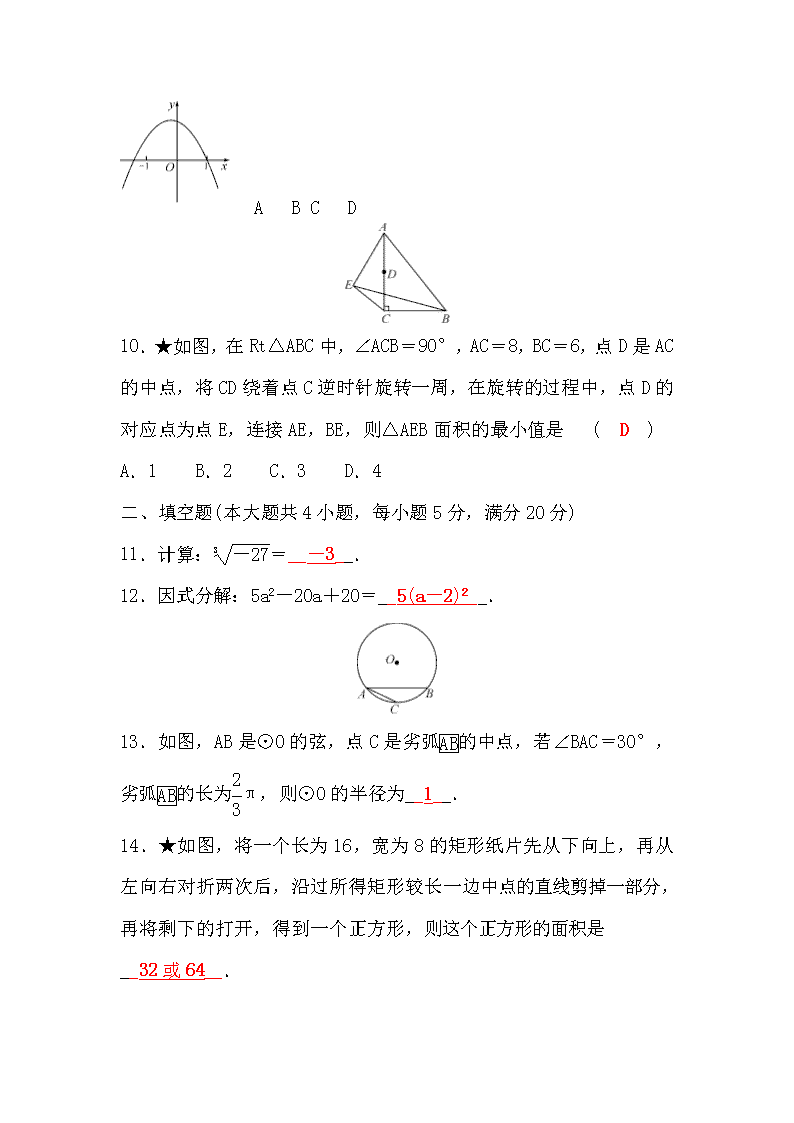
2021年安徽省初中学业水平考试数学模拟卷(三)(考试时间：120分钟　　满分：150分)一、选择题(本大题共10小题，每小题4分，满分40分)1．－2021的相反数是(　B　)A.－2021　B．2021　C．－　D．2．计算(x3y)2的结果是(　D　)A.x3y2B．x6yC．x5y2D．x6y23．由4个完全相同的小正方体组成的立体图形如图所示，则该立体图形的俯视图是(　B　)　4．2019年“十一”黄金周期间(7天)，北京市接待旅游总人数为920.7万人次，旅游总收入111.7亿元．其中111.7亿用科学记数法表示为(　C　)A.111.7×106B．11.17×109C.1.117×1010D．1.117×1085．不等式3x－3≤0的解集在数轴上表示正确的是(　D　) 6．将一把直尺与一块三角板如图放置，若∠1＝60°，则∠2为(　A　)A.150°B．120°C．100°D．60°7．某工厂为了降低生产成本进行技术革新，已知2018年的生产成本为a万元，以后每年的生产成本的平均降低率为x，则预计2020年的生产成本为(　B　)A.a(1－x%)2B．a(1－x)2C.(1－x)2D．a－a(x%)28．对九(1)班甲，乙，丙，丁四位同学在九年级三次阶段考试中的数学成绩进行分析，他们各自三次成绩的平均分x与方差s2如下表：甲乙丙丁平均分x142.5142.5141.3141.3方差s23.33.43.53.6若要选一位成绩突出且发挥更稳定的同学进行数学学习方法交流，则应该选(　A　)A．甲B．乙C．丙D．丁9．已知函数y＝－(x－m)(x－n)(其中m＜n)的图象如图所示，则一次函数y＝mx＋n与反比例函数y＝的图象可能是(　C　) 　　　10．★如图，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝6，点D是AC的中点，将CD绕着点C逆时针旋转一周，在旋转的过程中，点D的对应点为点E，连接AE，BE，则△AEB面积的最小值是(　D　)A．1B．2C．3D．4二、填空题(本大题共4小题，每小题5分，满分20分)11．计算：＝__－3__．12．因式分解：5a2－20a＋20＝__5(a－2)2__．13．如图，AB是⊙O的弦，点C是劣弧的中点，若∠BAC＝30°，劣弧的长为π，则⊙O的半径为__1__．14．★如图，将一个长为16，宽为8的矩形纸片先从下向上，再从左向右对折两次后，沿过所得矩形较长一边中点的直线剪掉一部分，再将剩下的打开，得到一个正方形，则这个正方形的面积是__32或64__． 　　　　三、(本大题共2小题，每小题8分，满分16分)15．计算：2sin60°＋(－2)－3－＋.解：原式＝2×－－2＋＝－.16．《孙子算经》是中国古代重要的数学著作之一．其中记载的“百鹿入城”问题很有趣．原文如下：今有百鹿入城，家取一鹿不尽，又三家共一鹿适尽，问城中家几何？大意为：现在有100头鹿进城，每家领取一头后还有剩余，剩下的鹿每三家分一头，则恰好取完．问城中共有多少户人家？解：设城中共有x户人家，依题意得，x＋＝100，解得x＝75，答：城中有75户人家．四、(本大题共2小题，每小题8分，满分16分)17．如图，在两建筑物之间有一旗杆，高15米，从A点经过旗杆顶点恰好看到矮建筑物的墙角C点，且俯角α为60° ，又从A点测得D点的俯角β为30°，若旗杆底部G点为BC的中点，求矮建筑物的高CD.解：过点D作DF⊥AF于点F，∵点G是BC中点，EG∥AB，∴EG是△ABC的中位线，∴AB＝2EG＝30米，在Rt△ABC中，∵∠CAB＝90－∠α＝30°，∴BC＝AB×tan∠BAC＝30×＝10米．在Rt△AFD中，∵AF＝BC＝10米，∴FD＝AF·tanβ＝10×＝10米，∴CD＝AB－FD＝30－10＝20米．18．如图，在由边长均为1个单位长度的小正方形组成的网格中，给出了格点△ABC和△DEF(顶点为网格线的交点)，以及经过格点的直线m.(1)画出△ABC关于直线m对称的△A1B1C1；(2)将△DEF先向左平移5个单位长度，再向下平移4个单位长度，画出平移后得到的△D1E1F1;(3)求∠A＋∠E＝______°. 解：(1)如图所示△A1B1C1，即为所求．(2)如图所示△D1E1F1，即为所求．(3)45.五、(本大题共2小题，每小题10分，满分20分)19．将一张正方形纸片剪成四个大小、形状一样的小正方形(如图所示)，记为第一次操作，然后将其中的一片又按同样的方法剪成四小片，记为第二次操作，如此循环进行下去．请将下表中空缺的数据填写完整，并解答所提出的问题：操作次数1234…正方形个数47____________…(1)如果剪100次，共能得到______个正方形；(2)如果剪n次共能得到bn个正方形，试用含有n，bn的等式表示它们之间的数量关系______；(3)若原正方形的边长为1，设an表示第n次所剪的正方形的边长，试用含n的式子表示an______； (4)试猜想a1＋a2＋a3＋a4＋…＋an－1＋an与原正方形边长的数量关系，并用等式写出这个关系______．解：表中填：10　13.(1)301.(2)bn＝3n＋1.(3)an＝.(4)a1＋a2＋a3＋a4＋…＋an－1＋an＝1－.20．如图，在四边形ABCD中，AB＝DC，点E是AB边上一点，CE＝AB，∠A＋∠ADC＝180°，DF⊥BC，垂足为点F，交CE于点G，连接DE，EF.(1)四边形ABCD是平行四边形吗？请说明理由；(2)求证：∠AED＝90°－∠DCE；(3)若点E是AB边的中点，求证：∠EFB＝∠DEF.(1)解：四边形ABCD是平行四边形，理由如下：∵∠A＋∠ADC＝180°，∴AB∥CD，且AB＝CD，∴四边形ABCD是平行四边形． (2)证明：∵CE＝AB，AB＝CD，∴CE＝CD，∴∠CDE＝∠CED＝＝90°－∠DCE，∵CD∥AB，∴∠AED＝∠CDE＝90°－∠DCE.(3)证明：延长DA，FE于点M，∵四边形ABCD是平行四边形，∴AD∥BC，且DF⊥BC，∴DF⊥AD，∠M＝∠EFB，∵∠M＝∠EFB，AE＝BE，∠AEM＝∠FEB，∴△AEM≌△BEF(AAS)，∴ME＝EF，且DF⊥DM，∴ME＝DE＝EF，∴∠M＝∠MDE，∴∠DEF＝∠M＋∠MDE＝2∠M，∴∠EFB＝∠DEF.六、(本题满分12分)21．写字是学生的一项基本功，为了了解某校学生的书写情况，随机对该校部分学生进行测试，测试结果分为A，B，C，D四个等级．根据调查结果绘制了下列两幅不完整的统计图，请你根据统计图提供的信息，回答以下问题： (1)这次调查的学生数有______人，把条形统计图补充完整；(2)若该校共有2000名学生，估计该校书写等级为“D级”的学生约有______人；(3)随机抽取了4名等级为“A级”的学生，其中有3名女生，1名男生，现从这4名学生中任意抽取2名，用列表或画树状图的方法，求抽到的两名学生都是女生的概率．　解：(1)50.补全统计图如图所示．(2)360.(3)列表如下：男女1女2女3男(女1，男)(女2，男)(女3，男)女1(男，女1)(女2，女1)(女3，女1)女2(男，女2)(女1，女2)(女3，女2)女3(男，女3)(女1，女3)(女2，女3)∵共有12种等可能的结果，抽到的两名学生都是女生的结果有6种．∴恰好抽到的两名学生都是女生的概率为＝. 七、(本题满分12分)22．小张在网上销售一种成本为20元/件的T恤衫，销售过程中的其他各种费用(不再含T恤衫成本)总计40(百元)，若销售价格为x(元/件)，销售量为y(百件)，当30≤x≤50时，y与x之间满足一次函数关系，且当x＝30时，y＝5，有关销售量y(百件)与销售价格x(元/件)的相关信息如下：销售量y(百件)______y＝销售价格x(元/件)30≤x≤5050≤x≤60(1)请在表格中直接写出当30≤x≤50时，y与x的函数关系式；(2)求销售这种T恤衫的纯利润w(百元)与销售价格x(元/件)的函数关系式；(3)销售价格定为多少元/件时，获得的利润最大？最大利润是多少？解：(1)y＝－x＋8.(2)当30≤x≤50时，w＝(x－20)(－0.1x＋8)－40＝－0.1x2＋10x－200；当50＜x≤60时，w＝(x－20)·－40＝－＋110.综上，w＝(3)当30≤x≤50时，w＝－0.1x2＋10x－200＝－0.1(x－50)2＋50，∴当x＝50时，w取得最大值50(百元)； 当50＜x≤60时，w＝－＋110，∵－3000＜0，∴w随x的增大而增大，当x＝60时，w取得最大值60(百元)，∴销售价格定为60元/件时，获得的利润最大，最大利润是60百元．八、(本题满分14分)23．已知，在△EFG中，∠EFG＝90°，EF＝FG，且点E，F分别在矩形ABCD的边AB，AD上．(1)如图①，当点G在CD上时，求证：△AEF≌△DFG；(2)如图②，若F是AD的中点，FG与CD相交于点N，连接EN，求证：EN＝AE＋DN；(3)如图③，若AE＝AD，EG，FG分别交CD于点M，N，求证：MG2＝MN·MD.图①图②图③证明：(1)∵四边形ABCD是矩形，∴∠A＝∠D＝90°，∴∠AEF＋∠AFE＝90°，∵∠EFG＝90°，∴∠AFE＋∠DFG＝90°，∴∠AEF＝∠DFG，∵EF＝FG，∴△AEF≌△DFG(AAS). (2)如图②，延长NF，EA相交于点H，∴∠AFH＝∠DFN，由(1)知，∠EAF＝∠D＝90°，∴∠HAF＝∠D＝90°，∵点F是AD的中点，∴AF＝DF，∴△AHF≌△DNF(ASA)，∴AH＝DN，FH＝FN，∵∠EFN＝90°，∴EH＝EN，∵EH＝AE＋AH＝AE＋DN，∴EN＝AE＋DN.(3)如图③，过点G作GP⊥AD交AD的延长线于P，∴∠P＝90°，同(1)的方法得，△AEF≌△PFG(AAS)，∴AF＝PG，AE＝PF，∵AE＝AD，∴PF＝AD，∴AF＝PD，∴PG＝PD，∵∠P＝90°，∴∠PDG＝45°，∴∠MDG＝45°，在Rt△EFG中，EF＝FG，∴∠FGE＝45°，∴∠FGE＝∠GDM，∵∠GMN＝∠DMG，∴△MGN∽△MDG， ∴＝，∴MG2＝MN·MD.