北京市东城区2006~2007学年度第二学期综合练习（一） 11页

北京市东城区2006~2007学年度第二学期综合练习（一）‎ 初三数学 本试卷分第I卷（选择题）和第II卷（填空题、解答题）两部分。‎ ‎ ‎ 第I卷（选择题32分）‎ 一、选择题：（本题共8个小题，每小题4分，共32分。）‎ 在每小题给出的四个选项中，只有一个是符合题目要求的。‎ ‎1、－2的平方为 ‎ A. 4 B. －‎4 ‎C. D. ‎ ‎2、随着中国综合国力的提升，全球学习汉语的人数不断增加，据报道2006年海外学习汉语的学生人数已达到48500000人，用科学记数法表示正确的是 ‎ A. B. C. D. ‎ ‎3、在函数中，自变量x的取值范围是 ‎ A. B. C. D. ‎ ‎4、已知，则的值为 ‎ A. －2 B. C. D. 1‎ ‎5、在实数范围内定义一种运算“*”，其规则为，根据这个规则，方程的解为 ‎ A. B. C. D. ‎ ‎6、如图，直线l与半径为‎5cm的⊙O相交于A、B两点，且与半径OC垂直，垂足为H。若，l要与⊙O相切，则l应向下平移 ‎ A. ‎1cm B. ‎2cm C. ‎3cm D. ‎‎4cm ‎7、从1，2，3，4，5五个数中任意取出2个数做加法，其和为偶数的概率是 ‎ A. B. C. D. ‎ ‎8、将正奇数按下表排成5列：‎ ‎ ‎ 第一列 第二列 第三列 第四列 第五列 第一行 ‎ ‎ ‎1‎ ‎3‎ ‎5‎ ‎7‎ 第二行 ‎15‎ ‎13‎ ‎11‎ ‎9‎ ‎ ‎ 第三行 ‎ ‎ ‎17‎ ‎19‎ ‎21‎ ‎23‎ 第四行 ‎31‎ ‎29‎ ‎27‎ ‎25‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎…‎ ‎…‎ ‎…‎ ‎ ‎ 根据上面规律，2007应在 A. 125行，3列 B. 125行，2列 C. 251行，2列 D. 251行，5列 ‎ ‎ 第II卷（填空题16分，解答题72分）‎ 二、填空题：（本大题共4小题，每小题4分，共16分。）‎ 把答案填在题中的横线上。‎ ‎9、把因式分解的结果是___________________。‎ ‎10、一个袋中装有6个红球、4个黑球、2个白球，每个球除颜色外完全相同，从袋中任意摸出一个球，那么摸出______________球的可能性最大。‎ ‎11、已知圆心在y轴上的两圆相交于两点，那么______________。‎ ‎12、小明把8个棱长为1分米的正方体摆在课桌上（如图所示），然后把露出的表面都涂上颜色，则被他涂上颜色部分的面积为______________。‎ ‎ ‎ 三、解答题（本大题共6小题，每小题5分，共30分）‎ ‎13、计算：。‎ ‎14、解不等式组：‎ ‎15、解分式方程：‎ ‎16、已知：如图，在菱形ABCD中，分别延长AB、AD到E、F，使得，连结EC、FC。‎ ‎ 求证：‎ ‎17、已知，求代数式的值。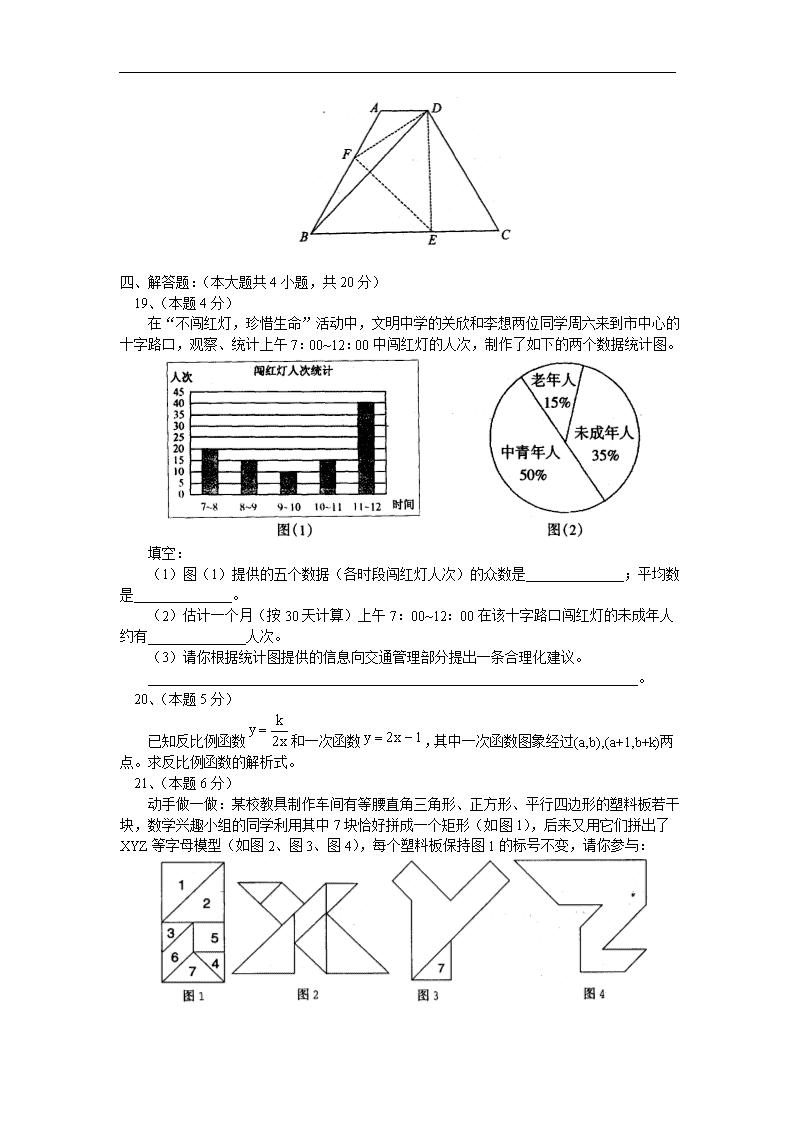‎ ‎18、如图，等腰梯形ABCD中，AD∥BC，∠DBC＝45°，翻折梯形ABCD，使点B与点D重合，折痕分别交AB、BC于点F、E。若。‎ ‎ 求BE的长；‎ ‎ ‎ 四、解答题：（本大题共4小题，共20分）‎ ‎19、（本题4分）‎ ‎ 在“不闯红灯，珍惜生命”活动中，文明中学的关欣和李想两位同学周六来到市中心的十字路口，观察、统计上午7：00~12：00中闯红灯的人次，制作了如下的两个数据统计图。‎ ‎ 填空：‎ ‎ （1）图（1）提供的五个数据（各时段闯红灯人次）的众数是______________；平均数是______________。‎ ‎ （2）估计一个月（按30天计算）上午7：00~12：00在该十字路口闯红灯的未成年人约有______________人次。‎ ‎ （3）请你根据统计图提供的信息向交通管理部分提出一条合理化建议。‎ ‎ ______________________________________________________________________。‎ ‎20、（本题5分）‎ 已知反比例函数和一次函数，其中一次函数图象经过(a,b),(a+1,b+k)两点。求反比例函数的解析式。‎ ‎21、（本题6分）‎ ‎ 动手做一做：某校教具制作车间有等腰直角三角形、正方形、平行四边形的塑料板若干块，数学兴趣小组的同学利用其中7块恰好拼成一个矩形（如图1），后来又用它们拼出了XYZ等字母模型（如图2、图3、图4），每个塑料板保持图1的标号不变，请你参与：‎ ‎（1）将图2中每块塑料板对应的标号填上去；‎ ‎（2）图3中，已画出了标号7的塑料板位置，请你适当画线，找出其他6块塑料板，并填上标号；‎ ‎（3）在图4中，画线找出7块塑料板位置，并填上标号。‎ ‎22、（本题5分）‎ ‎ 已知：如图，在Rt△ABC中，∠ACB＝90°，AC＝4，，以AC为直径的⊙O交AB于点D，点E是BC的中点，OB、DE交于点F。‎ ‎ （1）求证：DE是⊙O的切线；‎ ‎ （2）求EF：FD的值。‎ ‎ ‎ 五、解答题：（本大题共3小题，共22分）‎ ‎23、（本题6分）‎ 在四边形ABCD中，对角线AC平分∠DAB。‎ ‎（1）如图1，当∠DAB＝120°，∠B＝∠D＝90°时，求证：AB＋AD＝AC。‎ ‎（2）如图2，当∠DAB＝120°，∠B与∠D互补时，线段AB、AD、AC有怎样的数量关系？写出你的猜想，并给予证明；‎ ‎（3）如图3，当∠DAB＝90°，∠B与∠D互补时，线段AB、AD、AC有怎样的数量关系？写出你的猜想，不需证明。‎ ‎24、（本题8分）‎ ‎ 已知：如图，抛物线经过直线与坐标轴的两个交点A、B，此抛物线与x轴的另一个交点为C，抛物线的顶点为D。‎ ‎ （1）求此抛物线的解析式；‎ ‎ （2）点M为抛物线上的一个动点，求使△ABM与△ABD的面积相等的点M的坐标。‎ ‎25、（本题8分）‎ ‎ 我们给出如下定义：如果一个三角形的一个内角等于另一个内角的2倍，我们称这样的三角形为“倍角三角形”。在△ABC中，∠A、∠B、∠C所对的边分别为a、b、c。‎ ‎ （1）若∠A＝2∠B，且∠A＝60°，求证：‎ ‎ （2）如果对于任意的倍角三角形ABC（如图），其中∠A＝2∠B，关系式是否仍然成立？请证明你的结论；‎ ‎ （3）试求出一个倍角三角形的三条边的长，使这三条边长恰为三个连续的正整数。‎ ‎ ‎ ‎ ‎ 北京市东城区2006~2007学年度第二学期综合练习（一）‎ 初三数学参考答案及评分标准 ‎ ‎ 一、选择题（共8小题，每小题4分，共32分）‎ ‎1~5 ACDBD 6~8 BCD ‎ ‎ 二、填空题（本大题共4小题，每小题4分，共16分）‎ ‎9、 10、红 11、－2 12、25‎ ‎ ‎ 三、解答题（本大题共6小题，每小题5分，共30分）‎ ‎13、解：‎ ‎ 4分 ‎ 5分 ‎14、解：‎ 由①，得， 2分 由②，得。 4分 ‎∴原不等式组的解集为 5分 ‎15、解： 2分 ‎ 3分 经检验：是原方程的解。 4分 ‎∴原方程的解为 5分 ‎16、证明：在菱形ABCD中，BC＝DC，∠ABC＝∠ADC。‎ ‎∴180°－∠ABC＝180°－∠ADC。‎ 即∠EBC＝∠FDC。 2分 在△EBC和△FDC中，‎ ‎ 4分 ‎ 5分 ‎17、解：‎ ‎ 2分 ‎ 3分 ‎ ∵∴ 4分 ‎ 原式＝1。 5分 ‎18、解：由题意得△BFE≌△DFE，‎ ‎∴DE＝BE。 1分 ‎∵在△BDE中，DE＝BE，∠DBE＝45°，‎ ‎∴∠BDE＝∠DBE＝45°。‎ ‎∴∠DEB＝90°，即DE⊥BC。 2分 在等腰梯形ABCD中，AD＝2，BC＝8，‎ 过A作AG⊥BC于G，‎ ‎∴四边形AGED是矩形。‎ 则有GE＝AD＝2。 3分 在Rt△ABG和Rt△DCE中，AB＝DC，AG＝DE，‎ ‎∴BG＝EC。 4分 ‎∴BE＝5。 5分 ‎ ‎ 四、解答题：（本大题共4小题，共20分）‎ ‎19、（本题4分）‎ ‎ （1）15，20． 2分 ‎ （2）1050． 3分 ‎ （3）加强对11~12点时段的交通管理。 4分 ‎（加强对中青年人（或未成年人）的交通安全教育，其它合理建议，酌情给分）‎ ‎20、（本题5分）‎ 解：∵一次函数的图象经过（a,b）和（a+1,b+k）两点，‎ ‎∴有 3分 解得k＝2。 4分 ‎∴反比例函数的解析式为 5分 ‎21、（本题6分）‎ ‎（每图2分，共6分）‎ ‎22、（本题5分）‎ ‎（1）证明：连结CD（如图）， 1分 则∠ADC＝∠BDC＝90°。‎ ‎∵E是BC的中点，‎ ‎∴DE＝BE＝EC。 2分 ‎∴∠EDC＝∠ECD。‎ ‎∵OC＝OD，‎ ‎∴∠ODC＝∠OCD。‎ ‎∴∠EDC＋∠ODC＝∠ECD＋∠OCD。‎ 即∠EDO＝∠ACB。‎ ‎∵∠ACB＝90°，‎ ‎∴∠EDO＝90°。‎ ‎∴OD⊥DE。‎ 即DE是⊙O的切线。 3分 ‎（也可以连结OE，由证明△ODE≌△OCE证明OD⊥DE）‎ ‎（2）解：连结OE。则△OEF∽△BDF。‎ 在Rt△ABC中，AC＝4，，则AB＝8，∠ABC＝30°。‎ ‎∴OE＝4，∠A＝60°。 4分 ‎∴△AOD是边长为2的等边三角形。‎ ‎∴AD＝2，BD＝AB－AD＝6。‎ ‎∴EF：FD＝OE：BD＝4：6＝2：3。 5分 ‎ ‎ 五、解答题：（本大题共3小题，共22分）‎ ‎23、（本题6分）‎ ‎（1）解：在四边形ABCD中，‎ ‎∵AC平分∠DAB，∠DAB＝120°，‎ ‎∴∠CAB＝∠CAD＝60°。‎ ‎∵∠B＝∠D＝90°，‎ ‎∴∠ACB＝∠ACD＝30°。‎ 即AB＋AD＝AC。 2分 ‎（2）AB＋AD＝AC。 3分 证明如下：‎ 过C点分别作AD和AB延长线的垂线段，垂足分别为E、F（如图1）。‎ ‎∵AC平分∠DAB，‎ ‎∴CE＝CF。‎ ‎∵∠ABC＋∠D＝180°，∠ABC＋∠CBF＝180°，‎ ‎∴∠CBF＝∠D。‎ ‎∵∠CED＝∠CFB＝90°，‎ ‎∴△CED≌△CFB。‎ ‎∴ED＝BF。‎ ‎∴AD＋AB＝AE＋ED＋AB＝AE＋AB＋BF ‎ ＝AE＋AF。‎ 由（1）知AE＋AF＝AC，‎ ‎∴AB＋AD＝AC。 4分 ‎（3）（如图2）。 6分 ‎24、（本题8分）‎ 解：（1）直线与坐标轴的两个交点坐标分别是A（3，0）、B（0，3），抛物线经过A、B两点，‎ ‎ 2分 ‎∴抛物线的解析式为 3分 ‎（2）①作经过点D与直线平行的直线交抛物线于点M。‎ 则 直线DM的解析式为 由抛物线解析式得D（1，4）。‎ ‎∴t＝5。‎ 设M点的坐标为（m，－m＋5）。‎ ‎∵点M在抛物线上，‎ 解得m＝1或m＝2。‎ 当时，（1，4）是抛物线的顶点，故舍去；因此m＝2。‎ ‎∴M点的坐标为（2，3）。 5分 ‎②易求直线DM关于直线对称的直线l的解析式为 ‎，l交抛线物于M。 6分 设M点的坐标为 ‎∵点M在抛物线上，‎ 解得 ‎∴使△ABM与△ABD的面积相等的点M的坐标分别是（2，3），‎ ‎ 8分 ‎25、（本题8分）‎ ‎（1）证明：在△ABC中，∠A＝2∠B，且∠A＝60°，‎ ‎∴∠C＝90°，∠B＝30°。‎ 由勾股定理，得 ‎ 2分 ‎（2）关系式仍然成立。 3分 证明：如图，延长CA至点D，使AD＝AB＝c，连结BD。 4分 则△ABD为等腰三角形，∠D＝∠ABD。‎ ‎∵∠BAC为△ABD的一个外角，‎ ‎∴∠BAC＝2∠D。‎ 由已知，∠BAC＝2∠ABC，‎ ‎∴∠ABC＝∠D。‎ 又∠C为△ABC与△BDC的一个公共角，‎ 于是△ABC∽△BDC。 5分 ‎ 6分 ‎（3）若△ABC是倍角三角形，由∠A＝2∠B，应有，且 当时，设（n为大于1的正整数）‎ 代入，得，解得 有且满足∠A＝2∠B。‎ ‎（当及时，均不存在三条边长恰为三个连续正整数的倍角三角形。）‎ ‎∴边长为4，5，6的三角形为所求。 8分 ‎ ‎ ‎ ‎