- 854.06 KB
- 2021-11-06 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
课时训练(二十二) 相似三角形
(限时:35分钟)
|夯实基础|
1.[2019·淄博桓台县二模]已知ab=25,则a+bb的值为 ( )
A.25 B.35
C.23 D.75
2.[2019·上海徐汇区校级一模]下列四条线段中,不能成比例的是 ( )
A.a=4,b=8,c=5,d=10
B.a=2,b=25,c=5,d=5
C.a=1,b=2,c=3,d=4
D.a=1,b=2,c=2,d=4
3.[2018·重庆A卷]要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5 cm,6 cm和9 cm,另一个三角形的最短边长为2.5 cm,则它的最长边为 ( )
A.3 cm
B.4 cm
C.4.5 cm
D.5 cm
4.[2017·长春]如图K22-1,直线a∥b∥c,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F.若AB∶BC=1∶2,DE=3,则EF的长为 .
图K22-1
5.[教材题]如图K22-2,已知在△ABC中,D是边AC上的一点,∠CBD的平分线交AC于点E,且AE=AB,求证:AE2=AD·AC.
图K22-2
9
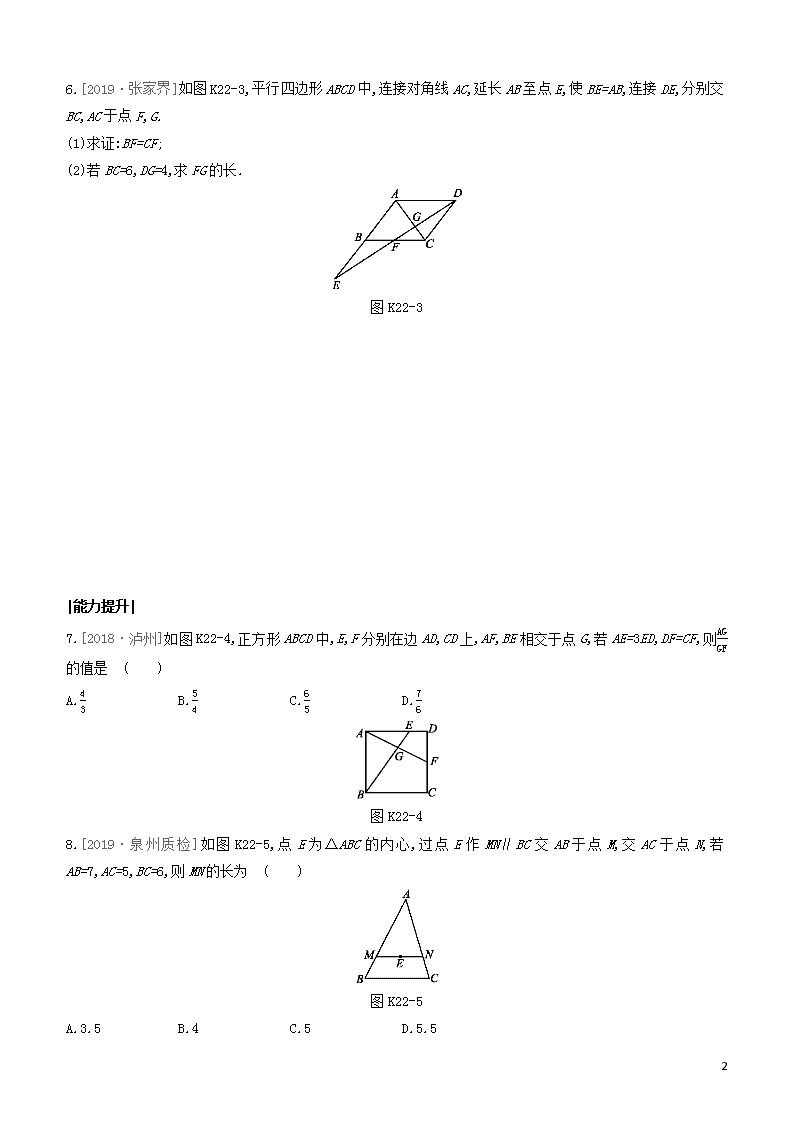
6.[2019·张家界]如图K22-3,平行四边形ABCD中,连接对角线AC,延长AB至点E,使BE=AB,连接DE,分别交BC,AC于点F,G.
(1)求证:BF=CF;
(2)若BC=6,DG=4,求FG的长.
图K22-3
|能力提升|
7.[2018·泸州]如图K22-4,正方形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若AE=3ED,DF=CF,则AGGF的值是 ( )
A.43 B.54 C.65 D.76
图K22-4
8.[2019·泉州质检]如图K22-5,点E为△ABC的内心,过点E作MN∥BC交AB于点M,交AC于点N,若AB=7,AC=5,BC=6,则MN的长为 ( )
图K22-5
A.3.5 B.4 C.5 D.5.5
9
9.[2018·包头]如图K22-6,在Rt△ACB中,∠ACB=90°,AC=BC,D是AB上的一个动点(不与点A,B重合),
图K22-6
连接CD,将CD绕点C顺时针旋转90°得到CE,连接DE,DE与AC相交于点F,连接AE.下列结论:
①△ACE≌△BCD;
②若∠BCD=25°,则∠AED=65°;
③DE2=2CF·CA;
④若AB=32,AD=2BD,则AF=53.
其中正确的结论是 .(填写所有正确结论的序号)
10.[2019·永州新田县三模]
【问题情境】
(1)古希腊著名数学家欧几里德在《几何原本》提出了射影定理,又称“欧几里德定理”:在直角三角形中,斜边上的高是两条直角边在斜边射影的比例中项,每一条直角边又是这条直角边在斜边上的射影和斜边的比例中项.射影定理是数学图形计算的重要定理.
其符号语言是:如图K22-7①,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,则:(1)CD2=AD·BD,(2)AC2=AB·AD,(3)BC2=AB·BD.请你证明定理中的结论(3)BC2=AB·BD.
【结论运用】
(2)如图②,正方形ABCD的边长为6,点O是对角线AC,BD的交点,点E在CD上,过点C作CF⊥BE,垂足为F,连接OF,
①求证:△BOF∽△BED;
②若BE=210,求OF的长.
图K22-7
9
|思维拓展|
11.[2017·攀枝花]如图K22-8,D是等边三角形ABC的边AB上的点,AD=2,BD=4.现将△ABC折叠,使得点C与点D重合,折痕为EF,且点E,F分别在边AC和BC上,则CFCE= .
图K22-8
12.[2019·乐山]在△ABC中,已知D是BC边的中点,G是△ABC的重心,过G点的直线分别交AB,AC于点E,F.
(1)如图K22-9①,当EF∥BC时,求证:BEAE+CFAF=1.
(2)如图②,当EF和BC不平行,且点E,F分别在线段AB,AC上时,(1)中的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.
(3)如图③,当点E在AB的延长线上或点F在AC的延长线上时,(1)中的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.
①
②
③
图K22-9
9
9
【参考答案】
1.D 2.C 3.C 4.6
5.证明:∵BE平分∠CBD,
∴∠DBE=∠CBE.
∵AE=AB,
∴∠ABE=∠AEB.
∵∠ABE=∠ABD+∠DBE,∠AEB=∠C+∠CBE,
∴∠ABD=∠C.
∵∠ABD=∠C,∠A=∠A,
∴△ABD∽△ACB,
∴ABAD=ACAB,即:AB2=AD·AC.
∵AE=AB,
∴AE2=AD·AC.
6.解:(1)证明:∵四边形ABCD是平行四边形,
∴AE∥CD,AB=CD,
∴∠EBF=∠DCF,∠BEF=∠CDF,
∵AB=BE,∴BE=CD,
∴△BEF≌△CDF,∴BF=CF.
(2)∵BF=CF,BC=6,∴CF=3.
∵AD∥BC,∴△ADG∽△CFG,
∴CFAD=FGDG,
即36=FG4,解得FG=2.
7.C [解析]因为正方形ABCD中,AE=3ED,DF=CF,所以设边长为4a,则AE=3a,ED=a,DF=CF=2a,
延长BE,CD交于点M,
易得△ABE∽△DME,
可得MD=43a,
9
因为△ABG∽△FMG,AB=4a,MF=103a,
所以AGGF=ABMF=65.
8.B
9.①②③ [解析]由题意易得∠BCD=∠ACE,由“边角边”证明△ACE≌△BCD,故①正确;
∵△ACE≌△BCD,
∴∠CAE=∠CBD=45°.
∵∠BCD=25°,∴∠ACE=∠BCD=25°,
∴∠AED=∠AEC-∠CED=(180°-25°-45°)-45°=65°,故②正确;
∵∠CAE=∠CED=45°,∠ACE=∠ACE,
∴△ACE∽△ECF,
∴ACEC=ECFC,即EC2=AC·FC,
在Rt△DCE中,DE2=2CE2=2FC·AC,
故③正确;
作DM⊥BC于点M,
∵AB=32,AD=2BD,
∴BD=2,AC=BC=3,
∴DM=BM=1,
∴CM=3-1=2,
∴DC=CE=5,
由③可知DE2=2CE2=2CF·CA,
∴2×(5)2=2×3×FC,
∴FC=53,
∴AF=3-53=43,故④错误.
10.解:(1)证明:∵CD⊥AB,
∴∠BDC=90°,
而∠CBD=∠ABC,
9
∴Rt△CBD∽Rt△ABC,
∴CB∶AB=BD∶BC,
∴BC2=AB·BD.
(2)①证明:∵四边形ABCD为正方形,
∴OC⊥BO,∠BCD=90°,
∴BC2=BO·BD.
∵CF⊥BE,
∴BC2=BF·BE.
∴BO·BD=BF·BE,
即BOBE=BFBD,
而∠OBF=∠EBD,
∴△BOF∽△BED.
②∵在Rt△BCE中,BC=6,BE=210,
∴CE=BE2-BC2=2,
∴DE=DC-CE=4.
在Rt△OBC中,OB=22BC=32,
∵△BOF∽△BED,
∴OFDE=BOBE,即OF4=32210,
∴OF=655.
11.54 [解析]由题易知∠A=∠B=∠EDF=60°,∴∠AED=∠FDB,
∴△AED∽△BDF,
∴EDDF=AE+ED+ADDF+BF+DB.由翻折易知EC=ED,FC=FD,
∴CFEC=BC+BDAC+AD,
∴CFEC=54.
12.解:(1)证明:∵G是△ABC的重心,
∴DGAG=12.
又∵EF∥BC,
9
∴BEAE=DGAG=12,CFAF=DGAG=12,
则BEAE+CFAF=12+12=1.
(2)(1)中结论成立,证明如下:如图,
过点A作AN∥BC交EF的延长线于点N,FE,CB的延长线相交于点M,
则BEAE=BMAN,CFAF=CMAN,
∴BEAE+CFAF=BMAN+CMAN=BM+CMAN.
∵D是BC的中点,∴BD=CD,
又∵BM+CM=BM+CD+DM,
∴BM+CM=BM+BD+DM=DM+DM=2DM,
∴BEAE+CFAF=2DMAN.
又∵DMAN=DGAG=12,
∴BEAE+CFAF=2×12=1,故结论成立.
(3)(1)中结论不成立,理由如下:如图,记AB的中点为M,连接CM,则C,G,M三点共线.
当点F在AC的延长线上时,BE=BM+ME>AE,
∴BEAE>1,则BEAE+CFAF>1.
∴结论不成立.
同理:当点E在AB的延长线上时,CFAF>1,
∴BEAE+CFAF>1,
∴结论不成立.
9