中考数学全程复习方略第六讲一次方程组课件 46页

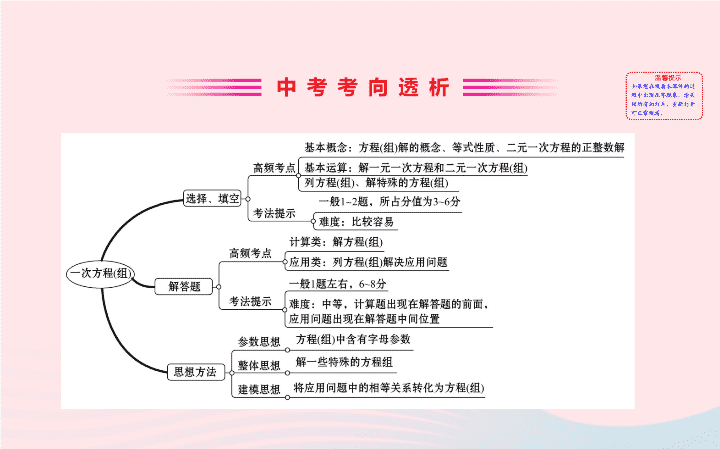
第六讲 　 一次方程 ( 组 ) 考点一　等式的性质、一次方程 ( 组 ) 的相关概念 【 主干必备 】 一、等式的性质 性质 1 等式两边加 ( 或减 ) 同一个数或同一个 ___________, 所得结果仍是等式 .  性质 2 等式两边乘 ( 或除以 ) 同一个数 ( 除数不 能为 0), 所得结果仍是 ___________.  式子 等式 二、一元一次方程 方程的概念 含有未知数的 ___________ 叫做方程 .  等式 方程的解 使方程左右两边的值 ___________ 的 未知数的值叫做方程的解 .  一元一次方程的概念 只含有 _________ 个未知数 , 且未知数 的最高次数是 ________ 的整式方程 , 叫做一元一次方程 .  相等 一 1 三、二元一次方程 ( 组 ) 二元一次方程的概念 含有 _________ 个未知数 , 并且含有未 知数的项的次数都是 ________ 的整式 方程叫做二元一次方程 .  二元一次方程组的概念 一般地 , 含有 ___________ 的未知数的 ___________ 二元一次方程合在一起 , 就组成了一个二元一次方程组 .  两 1 相同 两个 二元一次方程组的解 二元一次方程组的两个方程的 _____________, 叫做二元一次方 程组的解 .  公共解 【 微点警示 】 应用等式的性质时的两个注意 (1) 应用等式的性质进行等式变形 , 必须注意“都” , 不能漏项 . (2) 等式两边都除以同一个数或式子时 , 必须保证除数不为 0. 【 核心突破 】 【 例 1】 (1)(2019· 南充中考 ) 关于 x 的一元一次方程 +m=4 的解为 x=1, 则 a+m 的值为 ( 　 ) A.9 　　　 B.8 　　　 C.5 　　　 D.4 C (2)(2019· 菏泽中考 ) 已知 是方程组 的解 , 则 a+b 的值是 ( 　 ) A.-1 B.1 C.-5 D.5 A 【 明 · 技法 】 已知一次方程 ( 组 ) 的解 , 求方程 ( 组 ) 中字母的值的两种方法 (1) 代入法 : 当已知方程 ( 组 ) 的解时 , 把解代入方程 ( 组 ), 得到新的方程 ( 组 ), 再解新的方程 ( 组 ), 从而求出字母的值 . (2) 整体法 : 根据方程 ( 组 ) 中的未知数的系数特点 , 利用整体思想求某些字母的值 . 【 题组过关 】 1.(2019· 山西大同期末 ) 若 ma=mb, 则下列等式不一定 成立的是 ( 　 　 ) A.a=b B.ma+3=mb+3 C.-2ma=-2mb D.ma-2=mb-2 A 2.(2019· 湖北荆州松滋市期末 ) 某书上有一道解方程 的题 : ( 　 ) 处在印刷时被油墨盖住了 , 查后 面的答案知道这个方程的解是 x=2, 那么 ( 　 ) 处的数应 该是 ( 　 　 ) A.7 B.5 C.1 D.-2 C 3.(2019· 巴中中考 ) 已知关于 x,y 的二元一次方程组 的解是 则 a+b 的值是 ( 　 　 ) 世纪金榜导学号 A.1 B.2 C.-1 D.0 B 4. 若 x 2a-b+1 -3y a+4b-2 =7 是关于 x,y 的二元一次方程 , 那么 a+b 的值为 ________. 世纪金榜导学号  1 考点二　一次方程 ( 组 ) 的解法 【 主干必备 】 1. 解一元一次方程的一般步骤 去分母、 _____________ 、 ___________ 、 ________ __________ 、系数化为 1  去括号 移项 合并 同类项 2. 解二元一次方程组的方法步骤 二元一次方程组 _______________ 方程 . 消元 是解二元一次方程组的基本思路 , 方法有 ___________ 消元法和 ___________ 消元法 .  一元一次 代入 加减 【 微点警示 】 解一元一次方程去分母时 , 应注意不要漏项 , 移项时要注意变号 . 【 核心突破 】 【 例 2】 (1)(2018· 攀枝花中考 ) 解方程 : (2)(2019· 金华、丽水中考 ) 解方程组 【 思路点拨 】 (1) 去分母→去括号→移项→合并同类项→系数化为 1→ 得解 . (2) 把第一个方程先化简 , 然后使用加减法消元来解 ; 或者把第二个方程整体代入第一个方程 , 解出 x 的值 , 再代入第二个方程解出 y 的值 . 【 自主解答 】 略 【 明 · 技法 】 解二元一次方程组方法的选择 (1) 当方程组中某一个未知数的系数是 1 或者 -1 时 , 选用代入消元法较合适 . (2) 当方程组中某一个方程的常数项为 0 时 , 选用代入消元法较合适 . (3) 当两个方程中同一个未知数的系数相同或互为相反数时 , 选用加减消元法较合适 . (4) 当两个方程中同一个未知数的系数成整数倍关系时 , 选用加减消元法较合适 . 【 题组过关 】 1.(2019· 青岛李沧区期末 ) 解方程 去分母 结果正确的是 ( 　 　 ) A.3x=1-2x+2 B.3x=1-2x-2 C.3x=6-2x-2 D.3x=6-2x+2 D 2.(2019· 深圳福田区期末 ) 以方程组 的解 为坐标的点 (x,y) 在平面直角坐标系中的位置是 ( 　 　 ) A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 D 3. (2019· 广州三模 ) 若 x,y 为实数 , 且满足 (x+2y) 2 + =0, 则 x y 的值是 _______. 世纪金榜导学号  4. 解方程组 :(1)(2019· 山西中考 ) 世纪金榜导学号 (2)(2019· 青岛即墨期末 ) 【 解析 】 (1) 由 ① + ② 得 :4x=-8, 解得 x=-2, 将 x=-2 代入② , 得 :-2+2y=0, 解得 y=1, ∴ 原方程组的解为 (2) 将方程组整理成一般式得 ① +②, 得 :8x=16, 解得 x=2, 将 x=2 代入① , 得 :6+2y=6, 解得 y=0, 则方程组的解为 考点三　一次方程 ( 组 ) 的应用 【 主干必备 】 一次方程 ( 组 ) 实际应用的一般步骤 1. 审 审清题意 , 分清题中的已知量、未知量 2. 设 设 _____________, 设其中某个量为未知数 , 并注意单位 , 对含有两个未知量的问题 , 需设 两个未知数  未知数 3. 列 弄清题意 , 找出 _______________; 根据 _______________, 列方程 ( 组 )  4. 解 解方程 ( 组 ) 5. 验 检验结果是否 _______________  6. 答 写答案 ( 包括单位 ) 等量关系 等量关系 符合题意 【 微点警示 】 列方程时的三个注意点 (1) 设未知数时 , 单位要写清楚 . (2) 列方程时 , 方程两边所表示的量应该相同 , 并且各项的单位要一致 . (3) 对于求得的解 , 还要检验其是否符合实际意义 . 【 核心突破 】 【 例 3】 (1)(2018· 邵阳中考 ) 程大位是我国明朝商人 , 珠算发明家 . 他 60 岁时完成的 《 直指算法统宗 》 是东方古代数学名著 , 详述了传统的珠算规则 , 确立了算盘用法 . 书中有如下问题 : 一百馒头一百僧 , 大僧三个更无争 , 小僧三人分一个 , 大小和尚得几丁 . 意思是 : 有 100 个和尚分 100 个馒头 , 如果大和尚 1 人分 3 个 , 小和尚 3 人分 1 个 , 正好分完 , 大、 小和尚各有多少人 , 下列求解结果正确的是 ( 　 　 ) A A. 大和尚 25 人 , 小和尚 75 人 B. 大和尚 75 人 , 小和尚 25 人 C. 大和尚 50 人 , 小和尚 50 人 D. 大、小和尚各 100 人 (2)(2018· 长沙中考 ) 随着中国传统节日“端午节”的临近 , 东方红商场决定开展“欢度端午 , 回馈顾客”的让利促销活动 , 对部分品牌粽子进行打折销售 , 其中甲品牌粽子打八折 , 乙品牌粽子打七五折 , 已知打折前 , 买 6 盒甲品牌粽子和 3 盒乙品牌粽子需 600 元 ; 打折后 , 买 50 盒甲品牌粽子和 40 盒乙品牌粽子需要 5 200 元 . ① 打折前甲、乙两种品牌粽子每盒分别为多少元 ? ② 阳光敬老院需购买甲品牌粽子 80 盒 , 乙品牌粽子 100 盒 , 问打折后购买这批粽子比不打折节省了多少钱 ? 【 自主解答 】 ① 设打折前甲品牌粽子每盒 x 元 , 乙品牌 粽子每盒 y 元 , 根据题意得 : 解得 : 答 : 打折前甲品牌粽子每盒 40 元 , 乙品牌粽子每盒 120 元 . ②80×40+100×120-80×0.8×40-100×0.75×120= 3 640( 元 ). 答 : 打折后购买这批粽子比不打折节省了 3 640 元 . 【 明 · 技法 】 常见应用题类型及基本数量关系 常见类型 基本数量关系 行程问题 ( 路程 = 速度 × 时间 ) 相遇 问题 甲走的路程 + 乙走的路程 = 两地距离 常见类型 基本数量关系 行程问题 ( 路程 = 速度 × 时间 ) 追及 问题 同地不同时出发 : 前者走的路 程 = 追者走的路程 ; 同时不同地出发 : 前者走的路 程 + 两地距离 = 追者走的路程 航行 问题 顺水速度 = 静水速度 + 水流速 度 ; 逆水速度 = 静水速度 - 水流速 度 常见类型 基本数量关系 工程问题 工作总量 = 工作效率 × 工作时间 ; 各部分工作量之和 =1 销售问题 售价 = 标价 × 折扣 ; 销售额 = 售价 × 销量 ; 利润 = 售价 - 进价 ; 利润 = 进价 × 利润率 【 题组过关 】 1.(2019· 江西九江期末 ) 一个两位数 , 十位上的数字比 个位上的数字大 1, 若将个位与十位上的数字对调 , 得到 的新数比原数小 9, 设个位上的数字为 x, 十位上的数字 为 y, 根据题意 , 可列方程组为 ( 　 　 ) D 2.(2019· 岳阳中考 ) 我国古代的数学名著 《 九章算术 》 中有下列问题 :“ 今有女子善织 , 日自倍 , 五日织五尺 . 问日织几何 ?” 其意思为 : 今有一女子很会织布 , 每日加 倍增长 ,5 日共织布 5 尺 . 问每日各织多少布 ? 根据此问题 中的已知条件 , 可求得该女子第一天织布 ______ 尺 .