2020九年级数学上册 第4章 相似三角形阶段性测试（八）练习 （新版）浙教版 5页

阶 段 性 测 试(八)‎ ‎(见学生单册)‎ ‎[考查范围：相似三角形(4.1～4.4)]‎ 一、选择题(每小题4分，共24分)‎ ‎1．已知△ABC∽△A′B′C′，∠A＝50°，∠B＝100°，则∠C′的度数是(　A　)‎ A．30° B．50° C．30°或50° D．100°‎ ‎2．下列命题中正确的是(　C　)‎ A．所有的直角三角形都相似 B．所有的等腰三角形都相似 ‎ C．所有的等腰直角三角形都相似 D．以上结论都不对 ‎3．若ab＝mn，则下列比例式中错误的是(　C　)‎ A.＝ B.＝ C.＝ D.＝ 第4题图 ‎4．如图所示，在△ABC中，∠B＝90°，AB＝6，BC＝8，将△ABC沿DE折叠，使点C落在AB边上的C′处，并且C′D∥BC，则CD的长是(　A　)‎ A. B. C. D. 5‎ 第5题图 ‎5. 如图所示，已知点D，F在△ABC的边AB上，点E在边AC上，且DE∥BC，要使得EF∥CD，还需添加一个条件，这个条件可以是(　C　)‎ A.＝ B.＝ C.＝ D.＝ 第6题图 ‎6．如图所示，四边形ABCD是正方形，E是CD的中点，P是BC边上一点，下列条件中，不能推出△ABP与△ECP相似的是(　D　)‎ A．∠APB＝∠EPC B．∠APB＝∠APE＝60°‎ C．BP∶BC＝2∶3 D．P是BC的中点 二、填空题(每小题6分，共24分)‎ 第8题图 ‎7．已知a＝4，b＝9，则a，b的比例中项是__±6__．‎ ‎8．如图所示，添加一个条件，使△ADE∽△ACB：__∠ADE＝∠ACB(答案不唯一)__(写出一个即可)．‎ ‎9．如图所示，在△PAB中，M，N是AB上两点，且△PMN是等边三角形，△BPM∽△PAN，则∠APB的度数是__120°__．‎ ‎　　第9题图 ‎　第10题图 ‎10．如图所示，在平面直角坐标系中，四边形OABC是边长为2的正方形，顶点A，C分别在x，y轴的正半轴上．点Q在对角线OB上，且QO＝OC，连接CQ并延长CQ交边AB于点P.则点P的坐标为　P(2，4－2)　．‎ 三、解答题(5个小题，共52分)‎ 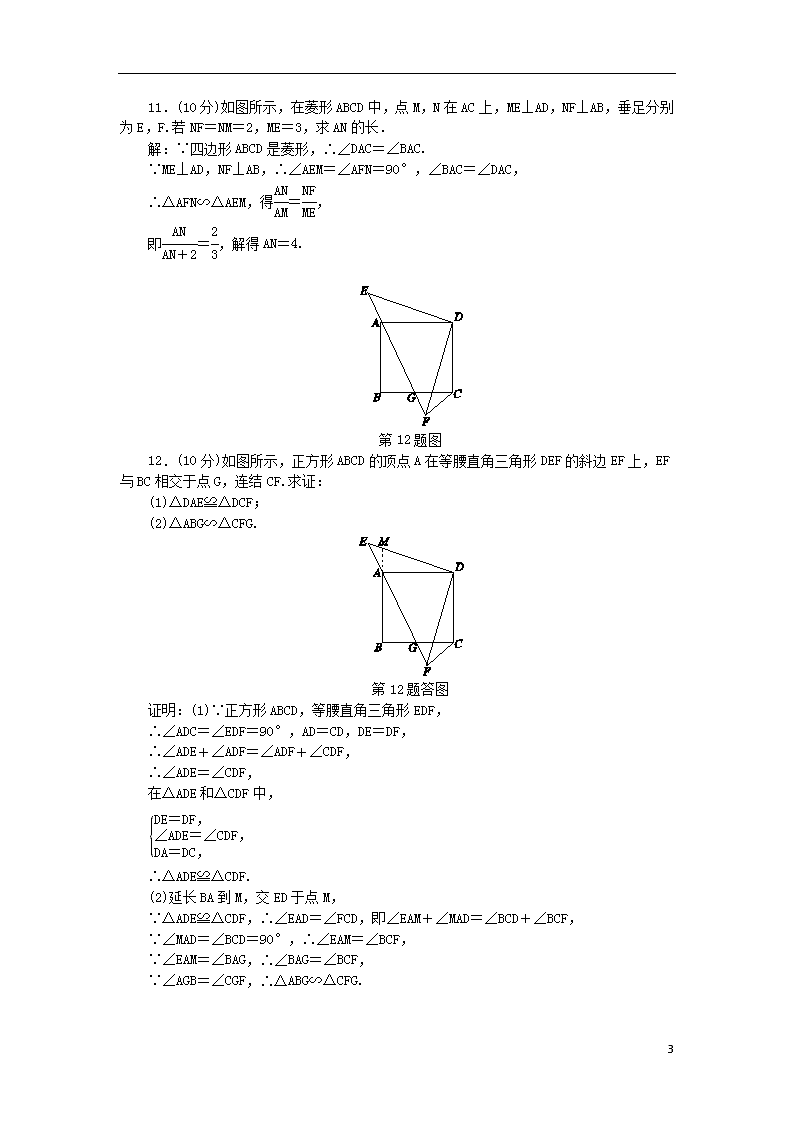第11题图 5‎ ‎11．(10分)如图所示，在菱形ABCD中，点M，N在AC上，ME⊥AD，NF⊥AB，垂足分别为E，F.若NF＝NM＝2，ME＝3，求AN的长．‎ 解：∵四边形ABCD是菱形，∴∠DAC＝∠BAC.‎ ‎∵ME⊥AD，NF⊥AB，∴∠AEM＝∠AFN＝90°，∠BAC＝∠DAC，‎ ‎∴△AFN∽△AEM，得＝，‎ 即＝，解得AN＝4.‎ 第12题图 ‎12．(10分)如图所示，正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上，EF与BC相交于点G，连结CF.求证：‎ ‎(1)△DAE≌△DCF；‎ ‎(2)△ABG∽△CFG.‎ 第12题答图 证明：(1)∵正方形ABCD，等腰直角三角形EDF，‎ ‎∴∠ADC＝∠EDF＝90°，AD＝CD，DE＝DF，‎ ‎∴∠ADE＋∠ADF＝∠ADF＋∠CDF，‎ ‎∴∠ADE＝∠CDF，‎ 在△ADE和△CDF中，‎ ‎∴△ADE≌△CDF.‎ ‎(2)延长BA到M，交ED于点M，‎ ‎∵△ADE≌△CDF，∴∠EAD＝∠FCD，即∠EAM＋∠MAD＝∠BCD＋∠BCF，‎ ‎∵∠MAD＝∠BCD＝90°，∴∠EAM＝∠BCF，‎ ‎∵∠EAM＝∠BAG，∴∠BAG＝∠BCF，‎ ‎∵∠AGB＝∠CGF，∴△ABG∽△CFG.‎ 5‎ 第13题图 ‎13．(12分)如图所示，CA⊥AB于点A，DB⊥AB于点B，AB＝‎12 m，AC＝‎4 m．一只蚂蚁由点B向点A爬行，每分钟爬行‎1 m，另一只蚂蚁由点B向点D爬行，每分钟爬行‎2 m．它们同时出发，点P，Q为它们在某一时刻的位置，爬行几分钟后，以A，C，P为顶点的三角形与以B，P，Q为顶点的三角形相似？请说明理由．‎ 解：设爬行t分钟后，以A，C，P为顶点的三角形与以B，P，Q为顶点的三角形相似．‎ ‎①当△ACP∽△BPQ时，＝，‎ 即＝，解得t＝4；‎ ‎②当△ACP∽△BQP时，＝，‎ 即＝， 解得t＝10.‎ 综上所述，当爬行4分钟或10分钟时，以A，P，C为顶点的三角形与以B，P，Q为顶点的三角形相似．‎ 第14题图 ‎14．(10分)如图所示，点A，B，C，D为⊙O上的四个点，AC平分∠BAD，AC交BD于点E，CE＝4，CD＝6，求AE的长．‎ 解：设AE＝x，则AC＝x＋4，‎ ‎∵AC平分∠BAD，‎ ‎∴∠BAC＝∠CAD.∵∠CDB＝∠BAC，‎ ‎∴∠CAD＝∠CDB，‎ 又∵∠DCE＝∠ACD，‎ ‎∴△ACD∽△DCE，‎ ‎∴＝，即＝，解得x＝5.‎ 即AE＝5.‎ 5‎ 第15题图 ‎15．(10分)如图所示，在平面直角坐标系xOy中，直线y＝－x＋3与x轴交于点C，与直线AD交于点A，点D的坐标为(0，1)．‎ ‎(1)求直线AD的解析式；‎ ‎(2)直线AD与x轴交于点B，若点E是直线AD上一动点(不与点B重合)，当△BOD与△BCE相似时，求点E的坐标．‎ 第15题答图 解：(1)设直线AD的解析式为y＝kx＋b，‎ 将A，D(0，1)代入，得 解得 故直线AD的解析式为y＝x＋1.‎ ‎(2)∵直线AD与x轴的交点为(－2，0)，‎ ‎∴OB＝2，‎ ‎∵点D的坐标为(0，1)，‎ ‎∴OD＝1，‎ ‎∵y＝－x＋3与x轴交于点C(3，0)，‎ ‎∴OC＝3，‎ ‎∴BC＝5.‎ ‎∵△BOD与△BCE相似，‎ ‎∴＝＝或＝，‎ ‎∴＝＝或＝，‎ ‎∴BE＝2，CE＝或CE＝，‎ ‎∴E(2，2)或.‎ 5‎