中考数学全程复习方略第一讲实数课件 59页

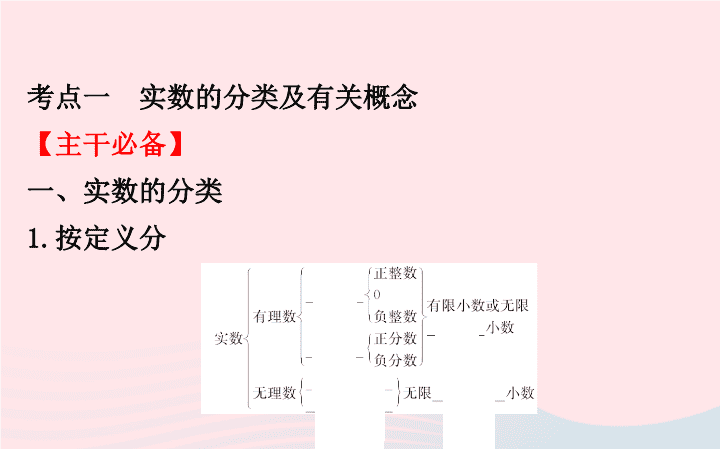
第一讲　 实　　数 考点一　实数的分类及有关概念 【 主干必备 】 一、实数的分类 1. 按定义分 2. 按性质分 二、实数的有关概念 名称 定义 性质 数轴 规定了 _____ 、 _______ 、 _________ 的直线 .  数轴上的点与实数一一对应 . 原点 正方向 单位长度 名称 定义 性质 相反 数 只有 _____ 不同 的两个数 , 即实 数 a 的相反数是 -a.  ① 若 a,b 互为相反数 , 则 a+b=0. ② 在数轴上 , 表示相反数的 两个数的点位于原点 _____, 且到原点的距离相等 .  绝对 值 在数轴上表示数 a 的点与原点的 _____, 记作 |a|.  符号 两侧 距离 名称 定义 性质 倒数 ________ 的两个数 互为倒数 , 非零实 数 a 的倒数为   ①ab=1⇔a,b 互为倒数 ; ②0 没有倒数 ; ③ 倒数等于本身的数是 1 和 -1. 乘积是 1 【 微点警示 】 关于 0:0 是有理数 ,0 是整数 ,0 是自然数 ,0 既不是正数 , 也不是负数 .0 的相反数和绝对值都等于它本身 ,0 没有倒数 . 【 核心突破 】 【 例 1】 (1)(2018· 菏泽中考 ) 下列各数 :-2,0, 0.020 020 002…,π, 其中无理数的个数是 ( 　 　 ) 　　　　　　　　　　　　　　　　　　 A.4 B.3 C.2 D.1 C (2)(2019· 眉山中考 ) 下列四个数中 , 是负数的是 ( 　 　 ) A.|-3| 　　 B.-(-3) 　　 C.(-3) 2 　　 D.- D (3)(2018· 日照中考 )|-5| 的相反数是 ( 　 　 ) A.-5 B.5 C. D.- A 【 明 · 技法 】 无理数常见的四种类型 (1) 开方开不尽的数 , 如 等 . (2) 有特定意义的数 , 如圆周率 π, 或化简后含有 π 的数 , 如 +8 等 . (3) 具有特定结构的数 , 如 0.101 001 000 1… 等 . (4) 某些三角函数 , 如 sin 60° 等 . 【 题组过关 】 1.(2019· 自贡中考 ) 实数 m,n 在数轴上对应点的位置如 图所示 , 则下列判断正确的是 世纪金榜导学号 ( 　 　 ) B A.|m|<1 　　　　 B.1-m>1 C.mn>0 D.m+1>0 2.(2019· 黄石中考 ) 下列四个数 :-3,-0.5, 中 , 绝对值最大的数是 ( 　 　 ) A.-3 　　　 B.-0.5 　　　 C. 　　　 D. A 3.(2019· 广州三模 ) 已知 :|x|=3,|y|=2, 且 x>y, 则 x-y 的值为 世纪金榜导学号 ( 　 　 ) A.5 　　　 B.1 　　　 C.5 或 1 　　　 D.-5 或 -1 C 考点二　科学记数法 【 主干必备 】 科学记数法 把一个数写成 ______ 的形式 ( 其中 1≤ |a|<10,n 为整数 ), 这种记数法称为科 学记数法 .  近似数 一个近似数 _________ 到哪一位 , 就说 这个近似数精确到哪一位 .  a×10 n 四舍五入 【 微点警示 】 对于含计数单位的数字用科学记数法表示时 , 应先把计数单位转换为数字 , 然后用大数或小数的科学记数法来表示 , 常用的计数单位有 :1 千 =10 3 ,1 万 =10 4 ,1 亿 =10 8 等 . 【 核心突破 】 【 例 2】 (2019· 眉山中考 ) 中国华为麒麟 985 处理器是 采用 7 纳米制程工艺的手机芯片 , 在指甲盖大小的尺寸 上塞进了 120 亿个晶体管 , 是世界上最先进的具有人工 智能的手机处理器 , 将 120 亿个用科学记数法表示为 ( 　 　 ) C A.1.2×10 9 个　　　　 B.12×10 9 个 C.1.2×10 10 个 D.1.2×10 11 个 【 明 · 技法 】 科学记数法中确定 n 的值的方法 (1) 当原数的绝对值≥ 10 时 ,n 等于原数的整数位数减去 1, 或等于原数变为 a 时 , 小数点移动的位数 . (2) 当原数的绝对值小于 1 时 ,n 是负整数 , 它的绝对值等于原数左起第 1 个非零数字前所有 0 的个数 ( 含小数点前的一个 0) 【 题组过关 】 1.(2019· 密云县模拟 )2019 年 1 月 3 日上午 10 点 26 分 , 中 国嫦娥四号探测器成功在月球背面软着陆 , 成为人类首 次在月球背面软着陆的探测器 , 首次实现月球背面与地 面站通过中继卫星通信 . 月球距离地球的距离约为 38 4000 km, 将 384 000 用科学记数法表示为 ( 　 　 ) A A.3.84×10 5 　　　　 B.384×10 3 C.3.84×10 3 D.0.384×10 6 2.(2019· 福田区二模 ) 由吴京特别出演的国产科幻大 片 《 流浪地球 》 自 2019 年 1 月放映以来实现票房与口碑 双丰收 , 票房有望突破 50 亿元 , 其中 50 亿元可用科学记 数法表示为 ____________ 元 . ( 　 　 )  A.0.5×10 10 　　　　　 B.5×10 8 C.5×10 9 D.5×10 10 C 3.(2019· 天水中考 ) 自然界中的数学不胜枚举 , 如蜜蜂 建造的蜂房既坚固又省料 , 其厚度为 0.000 073 米 , 将 0.000 073 用科学记数法表示为世纪金榜导学号 ( 　 　 ) A.73×10 -6 B.0.73×10 -4 C.7.3×10 -4 D.7.3×10 -5 D 4. 据测算 ,5 万粒芝麻才 200 克 , 则 1 粒芝麻有 _______ 千 克 .( 结果用科学记数法表示 )  4×10 -6 5.(2019· 攀枝花中考 ) 用四舍五入法将 130 542 精确到 千位 , 正确的是 世纪金榜导学号 ( 　 　 ) A.131 000 B.0.131×10 6 C.1.31×10 5 D.13.1×10 4 C 考点三　平方根、算术平方根、立方根 【 主干必备 】 平方根、算术平方根、立方根的定义及性质 名称 定义 性质 平方 根 如果 x 2 =a(a≥0), 那 么这个数 x 就叫做 a 的平方根 . 记作 ± 正数的平方根有两个 , 它 们互为 _______;_____ 没 有平方根 ;0 的平方根是 __.  相反数 负数 0 名称 定义 性质 算术 平方 根 如果 x 2 =a(x>0), 那么 这个正数 x 就叫做 a 的 算术平方根 . 记作 0 的算术平方根是 __.  立方 根 若 x 3 =a, 则 x 叫做 a 的立 方根 , 记作 正数有一个 ___ 立方根 ; 0 的立方根是 0; 负数有 一个 ___ 立方根 .  0 正 负 【 微点警示 】 只有非负数才有平方根 , 而一个非负数的算术平方根仍是非负数 , 负数没有平方根和算术平方根 , 但是负数有立方根 . 【 核心突破 】 【 例 3】 (1)(2018· 荆门中考 )8 的相反数的立方根是 ( 　 　 ) A.2 　　　 B. 　　　 C.-2 　　　 D.- C (2)(2018· 巴彦淖尔中考 ) 的算术平方根的倒数是 ( 　 　 ) C 【 明 · 技法 】 (1) 平方根等于本身的数是 0. (2) 算术平方根等于本身的数是 0 和 1. (3) 立方根等于本身的数是 0 和 ±1. 【 题组过关 】 1.(2019· 安丘一模 ) 的立方根是 ( 　 　 ) A.8 　　　　　　　　 B.2 C.±8 D.±4 B 2.(2019· 荆门二模 ) 下列各数中 , 没有平方根的是 ( 　 　 ) A.-3 2 B.|-3| C.(-3) 2 D.-(-3) A 3.(2019· 临沂中考 ) 一般地 , 如果 x 4 =a(a≥0), 则称 x 为 a 的四次方根 , 一个正数 a 的四次方根有两个 . 它们互为 相反数 , 记为 ± 若 =10, 则 m=_____. 世纪金榜导学号  ±10 4.(2019· 开封兰考期中 ) 若 x+17 的立方根是 3, 则 3x-5 的平方根是 ____.  ±5 考点四　实数大小及无理数的估算 【 主干必备 】 实数大小比较的方法 (1) 数轴比较法 : 数轴上的两个数 ,_________ 边的数总 比左边的数 _________.  右 大 (2) 法则比较法 :___________>0> 负数 , 两个负数 , 绝对值 _________ 的反而小 .  (3) 作差比较法 :①a-b>0⇔a>b;②a-b<0⇔a________b; ③a-b=0⇔a________b.  正数 大 < = 【 核心突破 】 【 例 4】 (2019· 泰安中考 ) 在实数 |-3.14|,-3,- π 中 , 最小的数是 ( 　 　 ) A.- 　　 B.-3 　　 C.|-3.14| 　　 D.π B 【 明 · 技法 】 实数大小比较的其他方法 1. 倒数比较法 : 对任意正实数 a,b 有 ⇔ a0,b>0,a 2 >b 2 ⇔a>b.a<0,b<0,a 2 >b 2 ⇔ab>0⇔ 4. 作商比较法 :b>0 且 >1⇔a>b;b>0 且 <1⇔a0 且 =1⇔a=b. 5. 近似估算法 , 特殊值法 . 【 题组过关 】 1. 下列各实数中 , 最大的是 ( 　 　 ) A.π 　　 B.(-2 020) 0 　　 C.- 　 　 D.|-3| A 2.(2019· 南京中考 ) 下列整数中 , 与 10- 最接近的 是 世纪金榜导学号 ( 　 　 ) A.4 B.5 C.6 D.7 C 3.(2019· 九江月考 ) 若 a= b=-|- |,c=- 则 a,b,c 的大小关系是 ( 　 　 ) A.a0,b<0,a+b<0, 则四个数 a,b,-a,-b 的大小关系为 ____ _______( 用“ <” 号连接 ). 世纪金榜导学号  b<- a