2012初三数学一模题-西城 5页

北京市西城区2012年初三一模试卷 ‎ 数 学 2012. 5‎ 考生须知 ‎1．本试卷共5页，共五道大题，25道小题，满分120分。考试时间120分钟。‎ ‎2．在试卷和答题卡上准确填写学校名称、姓名和准考证号。‎ ‎3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效。‎ ‎4．在答题卡上，选择题、作图题用2B铅笔作答，其他试题用黑色字迹签字笔作答。‎ ‎5．考试结束，将本试卷、答题卡和草稿纸一并交回。‎ 一、选择题（本题共32分，每小题4分）‎ 下面各题均有四个选项，其中只有一个是符合题意的．‎ ‎1．的相反数是 A．6 B． C． D．‎ ‎2．国家体育场“鸟巢”建筑面积达258 000平方米，258 000用科学记数法表示应为 ‎ A．2.58×103 B．25.8×‎104 C．2.58×105 D．258×103‎ ‎3．正五边形各内角的度数为 ‎ A．72° B．108° 　C．120° D．144°‎ ‎4．抛掷两枚质地均匀的硬币，两枚硬币落地后，正面都朝上的概率是 A． B． C． D．‎ ‎5．如图，过上一点作的切线，交直径的 延长线于点D. 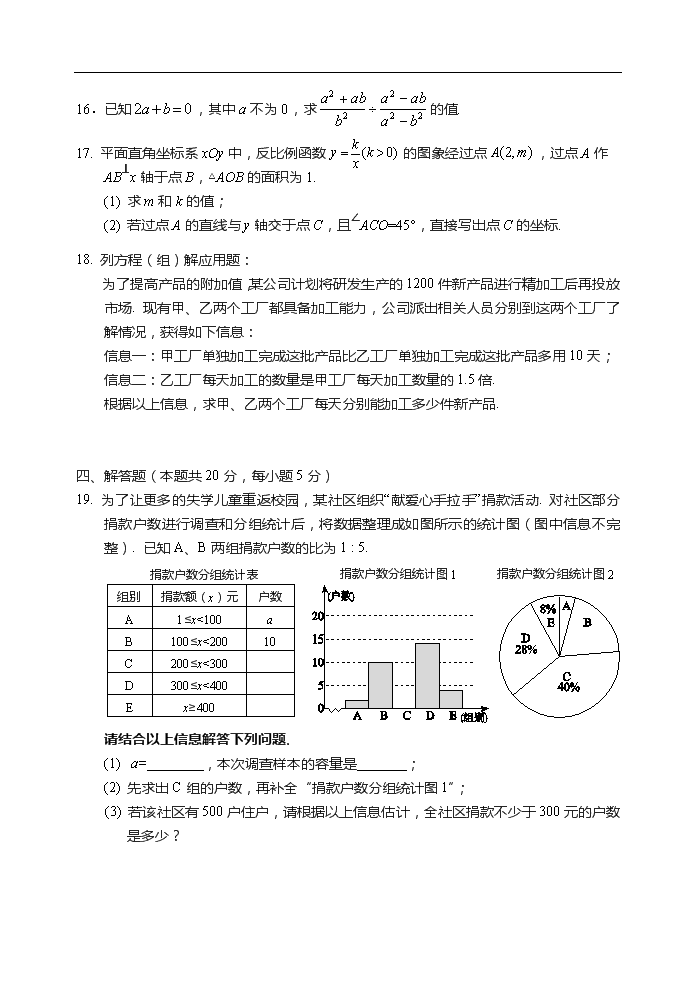若∠D=40°，则∠A的度数为 ‎ A．20° B．25°‎ ‎ C．30° D．40°‎ ‎6．某班体育委员统计了全班45名同学一周的 ‎ 体育锻炼时间(单位：小时)，并绘制了如图 ‎ 所示的折线统计图，下列说法中错误的是 A．众数是9 ‎ B．中位数是9 ‎ C．平均数是9 ‎ D．锻炼时间不低于9小时的有14人 ‎ ‎7．由个相同的小正方体堆成的几何体，其主视图、俯视图如下所示，则的最大值是 A．16 ‎ B．18‎ C．19 ‎ D．20‎ ‎8．对于实数c、d，我们可用min{ c，d }表示c、d两数中较小的数，如min{3，}=.若关于x的函数y = min{，}的图象关于直线对称，则a、t的值可能是 A．3，6 B．2，‎ ‎ C．2，6 D．，6‎ 二、填空题（本题共16分，每小题4分）‎ ‎9．函数中，自变量x的取值范围是 ．‎ ‎10．分解因式：= ．‎ ‎11．如图，正方形ABCD的面积为3，点E是DC边上一点，DE=1，‎ 将线段AE绕点A旋转，使点E落在直线BC上，落点记为F，‎ 则FC的长为 . ‎ ‎12．如图，直角三角形纸片ABC中，∠ACB=90°，AC=8，BC=6．‎ 折叠该纸片使点B与点C重合，折痕与AB、BC的交点分别 为D、E. (1) DE的长为 ；(2) 将折叠后的图形沿直线 AE剪开，原纸片被剪成三块，其中最小一块的面积等于 ．‎ 三、解答题（本题共30分，每小题5分）‎ ‎13．计算：．‎ ‎≥2x-4，‎ ‎14．解不等式组 并求它的所有的非负整数解. ‎ ‎15．如图，在△ABC中，AB=CB，∠ABC=90º，D为AB延长线 ‎ 上一点，点E在BC边上，且BE=BD，连结AE、DE、DC.‎ ‎ (1) 求证：△ABE≌△CBD；‎ ‎ (2) 若∠CAE=30º，求∠BCD的度数. ‎ ‎16．已知，其中a不为0，求的值. ‎ ‎17. 平面直角坐标系xOy中，反比例函数 的图象经过点，过点A作 ‎ AB⊥x轴于点B，△AOB的面积为1.‎ ‎(1) 求m和k的值；‎ ‎(2) 若过点A的直线与y轴交于点C，且∠ACO=45°，直接写出点C的坐标.‎ ‎18. 列方程（组）解应用题：‎ 为了提高产品的附加值，某公司计划将研发生产的1200件新产品进行精加工后再投放市场. 现有甲、乙两个工厂都具备加工能力，公司派出相关人员分别到这两个工厂了解情况，获得如下信息：‎ ‎ 信息一：甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天；‎ ‎ 信息二：乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.‎ 根据以上信息，求甲、乙两个工厂每天分别能加工多少件新产品.‎ 四、解答题（本题共20分，每小题5分）‎ ‎19. 为了让更多的失学儿童重返校园，某社区组织“献爱心手拉手”捐款活动. 对社区部分捐款户数进行调查和分组统计后，将数据整理成如图所示的统计图（图中信息不完整）. 已知A、B两组捐款户数的比为1 : 5.‎ 捐款户数分组统计图2‎ 捐款户数分组统计图1‎ ‎ 捐款户数分组统计表 组别 捐款额（x）元 户数 A ‎1≤x<100‎ a B ‎100≤x<200‎ ‎10‎ C ‎200≤x<300‎ D ‎300≤x<400‎ E x≥400‎ ‎ ‎ ‎ ‎ 请结合以上信息解答下列问题.‎ ‎(1) a= ，本次调查样本的容量是 ；‎ ‎ (2) 先求出C组的户数，再补全“捐款户数分组统计图‎1”‎；‎ ‎(3) 若该社区有500户住户，请根据以上信息估计，全社区捐款不少于300元的户数是多少？‎ ‎20．如图，梯形ABCD中，AD∥BC，，BC=2，‎ ‎，．‎ ‎(1) 求∠BDC的度数； ‎ ‎ (2) 求AB的长．‎ ‎21．如图，AC为⊙O的直径，AC=4，B、D分别在AC 两侧的圆上，∠BAD=60°，BD与AC的交点为E．‎ ‎ (1) 求点O到BD的距离及∠OBD的度数；‎ ‎ (2) 若DE=2BE，求的值和CD的长．‎ ‎22. 阅读下列材料：‎ 问题：如图1，在正方形ABCD内有一点P，PA=，PB=，PC=1，求∠BPC的度数．‎ 小明同学的想法是：已知条件比较分散，可以通过旋转变换将分散的已知条件集中在一起，于是他将△BPC绕点B逆时针旋转90°，得到了△BP′A（如图2），然后连结PP′．‎ 请你参考小明同学的思路，解决下列问题：‎ ‎(1) 图2中∠BPC的度数为 ；‎ ‎(2) 如图3，若在正六边形ABCDEF内有一点P，且PA=，PB=4，PC=2，则∠BPC的度数为 ，正六边形ABCDEF的边长为 ．‎ ‎ ‎ ‎ 图1 图2 图3‎ 五、解答题（本题共22分，第23题7分，第24题7分，第25题8分）‎ ‎23. 已知关于x的一元二次方程的一个实数根为 2． ‎ ‎ (1) 用含p的代数式表示q； ‎ ‎ (2) 求证：抛物线与x轴有两个交点； ‎ ‎ (3) 设抛物线的顶点为M，与 y轴的交点为E，抛物线 ‎ 顶点为N，与y轴的交点为F，若四边形FEMN的面积等于2，求p的值． ‎ ‎24．已知：在如图1所示的锐角三角形ABC中，CH⊥AB于点H，点B关于直线CH的对称点为D，AC边上一点E满足∠EDA=∠A，直线DE交直线CH于点F．‎ ‎ (1) 求证：BF∥AC；‎ ‎ (2) 若AC边的中点为M，求证：；‎ ‎ (3) 当AB=BC时（如图2），在未添加辅助线和其它字母的条件下，找出图2中所有与BE相等的线段，并证明你的结论．‎ ‎ 图1 图2‎ ‎25．平面直角坐标系xOy中，抛物线与x轴交于点A、点B，与y轴的正半轴交于点C，点 A的坐标为(1, 0)，OB=OC，抛物线的顶点为D． ‎ ‎ (1) 求此抛物线的解析式；‎ ‎ (2) 若此抛物线的对称轴上的点P满足∠APB=∠ACB，求点P的坐标；‎ ‎ (3) Q为线段BD上一点，点A关于∠AQB的平分线的对称点为，若，求点Q的坐标和此时△的面积．‎ ‎ ‎