鄂尔多斯专版2020中考数学复习方案第四单元三角形提分微课03常考相似模型课件 31页

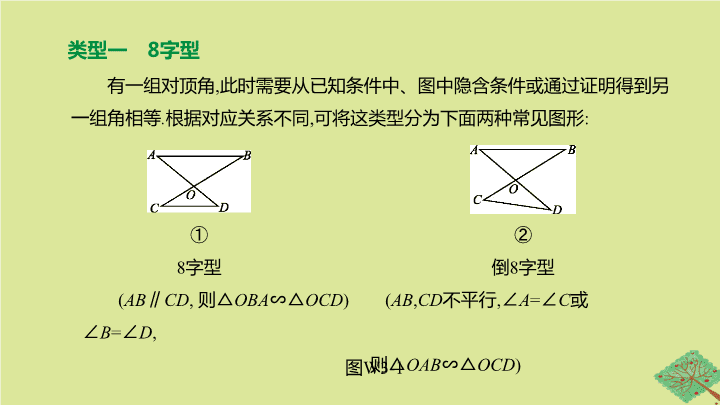
提分微课 （三） 常考相似模型 第四单元　三角形 　　相似三角形是几何中重要的证明模型之一 , 是全等三角形的推广 , 分析图形间的关系离不开数量的计算 . 相似和勾股是产生等式的主要依据 ( 其他依据还有面积法 , 三角函数等 ), 因此要掌握相似三角形的基本图形 , 体会其各种演变和联系 . 类型一　 8 字型 　　 有一组对顶角 , 此时需要从已知条件中、图中隐含条件或通过证明得到另一组角相等 . 根据对应关系不同 , 可将这类型分为下面两种常见图形 : 图 W 3 -1 　 ① 　　　　　　　　　　 ② 　　　　 8 字型 　　　　　　　　 倒 8 字型 　　 ( AB ∥ CD , 则 △ OBA ∽△ OCD ) 　　 ( AB , CD 不平行 , ∠ A = ∠ C 或∠ B = ∠ D , 则 △ OAB ∽△ OCD ) 图 W3-2 [ 答案 ] D 　 [ 解析 ] A 选项 , OB 和 CD 不是对应边 , 因此它们的比值不一定等于相似比 , 所以 A 选项不一定成立 ; B 选项 , ∠ A 和∠ C 是对应角 , 因此 α = β , 所以 B 选项不成立 ; C 选项 , 因为相似三角形的面积比等于相似比的平方 , 所以 C 选项不成立 ; D 选项 , 因为相似三角形的周长比等于相似比 , 所以 D 选项一定成立 . 故选 D . 图 W3-3 [ 答案 ] 6 图 W3-4 类型二　 A 字型 图 W3-5 　　 有一个公共角 , 外加另外一组对应角相等 . 根据对应关系不同 , 可将这类型分为下面两种常见图形 : 　 ① 　　　　　　　　　 ② 　 A 字型 　　　　　　　　 倒 A 字型 　 ( DE ∥ BC , 则 △ ADE ∽△ ABC ) 　　 ( DE , BC 不平行 , ∠ B = ∠ AED 或∠ C = ∠ ADE , 则 △ AED ∽△ ABC ) 4 . [2019· 镇江南徐中学模拟 ] 如图 W3-6, 在 △ ABC 中 , 点 D , E 分别在 AB , AC 上 , 且 DE ∥ BC. 若 AD =2, AB =3, DE =4, 则 BC 的长为 　　　　 . 图 W3-6 [ 答案 ] 6 5 . 如图 W3-7, 点 D , E 分别在 △ ABC 的边 AC , AB 上 , 且 AB =9, AC =6, AD =3 . 若使 △ ADE ∽ △ ABC , 则 AE 的长为 　　　　 .  图 W3-7 2 图 W3-8 解 :(1)3 图 W3-8 图 W3-8 类型三　子母型 图 W3-9 　　 有一个公共角 , 且公共角的一边为公共边 . 需要从已知条件、隐含条件中证明另外一组角相等 . 常见的图形如图① : ∠ ACD = ∠ B , ∠ ADC = ∠ ACB , 本图是最一般的子母型 . 如图② , ∠ ACB =90°, CD ⊥ AB , 图中的三个直角三角形都相似 , 这个图形也很常见 . 　　 ① 　　　　　　　　　　　　 ② 　　 ( ∠ ACD = ∠ B 或∠ ADC = ∠ ACB , 　　　　 △ ADC ∽△ ACB ∽△ CDB 　　 则 △ ACD ∽△ ABC ) 　　　　　　　　 [ 答案 ] C 7 . 如图 W3-10, 在 △ ABC 中 , 点 D 是 AB 边上的一点 , 若∠ ACD = ∠ B , AD =1, AC =2,△ ADC 的面积为 1, 则 △ BCD 的面积为 ( 　　 ) A . 1 B . 2 C . 3 D . 4 图 W3-10 图 W3-11 C 图 W3-12 [ 答案 ] D 　 [ 解析 ] 在 Rt△ ABC 中 , AB 为斜边 , CD 为斜边 AB 上的高 , 由 △ ADC ∽△ CDB 得 , CD 2 = AD · BD , ∴ CD =6 . 故选 D . 10 . 如图 W3-13, 在平面直角坐标系中 , 直线 y = kx +1 与 x 轴交于点 A , 与 y 轴交于点 C , 过点 C 的抛物线 y = ax 2 -(6 a -2) x + b 与直线 AC 交于另一点 B (4,3) . (1) 求抛物线的表达式 ; (2) 已知点 P 在 x 轴上 ( 点 P 不与点 O 重合 ), 连接 CP , 若 △ AOC 与 △ ACP 相似 , 求点 P 的坐标 ; (3) 已知 x 轴上一动点 Q ( m ,0), 连接 BQ , 若 △ ABQ 与 △ AOC 相似 , 直接写出 m 的值 . 图 W3-13 10 . 如图 W3-13, 在平面直角坐标系中 , 直线 y = kx +1 与 x 轴交于点 A , 与 y 轴交于点 C , 过点 C 的抛物线 y = ax 2 -(6 a -2) x + b 与直线 AC 交于另一点 B (4,3) . (2) 已知点 P 在 x 轴上 ( 点 P 不与点 O 重合 ), 连接 CP , 若 △ AOC 与 △ ACP 相似 , 求点 P 的坐标 ; 图 W3-13 10 . 如图 W3-13, 在平面直角坐标系中 , 直线 y = kx +1 与 x 轴交于点 A , 与 y 轴交于点 C , 过点 C 的抛物线 y = ax 2 -(6 a -2) x + b 与直线 AC 交于另一点 B (4,3) . (3) 已知 x 轴上一动点 Q ( m ,0), 连接 BQ , 若 △ ABQ 与 △ AOC 相似 , 直接写出 m 的值 . 图 W3-13 类型四　一线三等角 　　 基本图形 1: 三个相等的角的顶点在同一条直线上 , 称一线三等角模型 , 常见于等腰三角形或等边三角形的背景中 . 如图 W3-14 所示 : 图 W3-14 11 . 如图 W3-15, 在 △ ABC 中 , AB = AC , 点 P , D 分别是 BC , AC 边上的点 , 且∠ APD = ∠ B. (1) 求证 : AC · CD = CP · BP ; (2) 若 AB =10, BC =12, 当 PD ∥ AB 时 , 求 BP 的长 . 图 W3-15 11 . 如图 W3-15, 在 △ ABC 中 , AB = AC , 点 P , D 分别是 BC , AC 边上的点 , 且∠ APD = ∠ B. (2) 若 AB =10, BC =12, 当 PD ∥ AB 时 , 求 BP 的长 . 图 W3-15 　　 基本图形 2: 当在一线三等角模型中 , 三个等角为 90° 时 , 模型会变得更加特殊 , 如图 W3-16 . 图 W3-16 12 . 如图 W3-17, 正方形 ABCD 中 , 点 E , F , G 分别在 AB , BC , CD 上 , 且∠ EFG =90° . 求证 : △ EBF ∽△ FCG. 图 W3-17 证明 : ∵四边形 ABCD 为正方形 , ∴∠ B = ∠ C =90°, ∵∠ EFG =90°, ∴∠ BFE + ∠ CFG =90°, 而∠ BFE + ∠ BEF =90°, ∴∠ BEF = ∠ CFG , ∴ △ EBF ∽△ FCG. 13 . 如图 W3-18, AD ∥ BC , ∠ D =90°, DC =7, AD =2, BC =4 . 若在边 DC 上有点 P 使 △ PAD 和 △ PBC 相似 , 求 PD 的值 . 图 W3-18