鄂尔多斯专版2020中考数学复习方案第七单元图形的变化提分微课06利用“胡不归阿氏圆”解决最值问题课件 30页

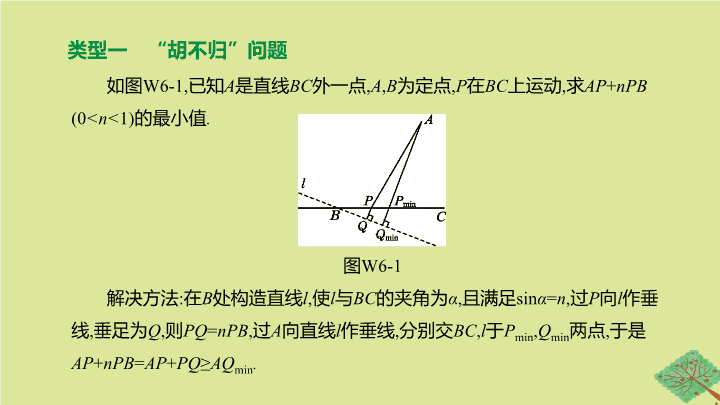
提分微课（六） 利用“胡不归、阿氏圆”解决 “ PA + n·PB ” 型的最值问题 第七单元　图形的变化 “ 胡不归 ” 和 “ 阿氏圆 ” 问题都是一类解决 “ PA + n · PB ”( n 为常数且 n ≠1) 型的最值问题 . 两类问题所蕴含的都是数学的转化思想 , 即将 nPB 的长度转化为某条具体线段 PC 的长度 , 进而根据 “ 垂线段最短或两点之间线段最短 ” 的原理构造最短距离 . 动点 P 在直线上运动的可用 “ 胡不归 ” 问题模型 , 动点 P 在圆周上运动的可用 ” 阿氏圆 ” 问题模型 . 类型一　“胡不归”问题 如图 W6-1, 已知 A 是直线 BC 外一点 , A , B 为定点 , P 在 BC 上运动 , 求 AP + nPB (0