九年级下册数学教案 2-2 第1课时 二次函数y=x2和y=-x2的图象与性质2 北师大版 3页

‎2.2 二次函数的图象与性质 第1课时 二次函数y=ax2的图象与性质 ‎【教学目标】‎ ‎(一)教学知识点 能够利用描点法作出函数的图象，并根据图象认识和理解二次函数的性质；比较两者的异同.‎ ‎(二)能力训练要求：经历探索二次函数图象的作法和性质的过程，获得利用图象研究函数性质的经验.‎ ‎（三）情感态度与价值观：通过学生自己的探索活动，达到对抛物线自身特点的认识和对二次函数性质的理解. ‎ ‎【重、难点】‎ 重点 ：会画y=ax2的图象，理解其性质。‎ 难点：描点法画y=ax2的图象，体会数与形的相互联系。 ‎ ‎【导学流程】 ‎ 一、自主预习（用时15分钟）‎ ‎1.创设教学情境 我们在教学了正比例函数、一次函数、反比例函数的定义后，都借助图像研究了它们的性质.而上节课我们所学的二次函数的图象是什么呢？本节课我们将从最简单的二次函数y=x2入手去研究 ‎ 2.出示教学目标 ‎3.学生自主教学，完成预习题 ‎1.作函数y=x2的图象 ‎ 回顾作函数图象的一般步骤：列表、描点、连线.‎ ‎(1)观察y= x2的表达式，选择适当的x值，并计算相应的y值，完成下表：（图象是未知的，所以应根据自变量的取值，x为任何实数，选取一些有代表性、方便计算的x值，如：几个负整数、0、几个正整数）‎ x ‎-3‎ ‎-2‎ ‎-1‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ y=x2‎ ‎9‎ ‎4‎ ‎1‎ ‎0‎ ‎1‎ ‎4‎ ‎9‎ ‎(2)在直角坐标系中描点．（按x的值从小到大，从左到右描点）‎ ‎(3)用光滑的曲线连接各点，便得到函数y=x2的图象．（能用直线连接吗？）‎ ‎4.组内交流质疑 二、展示交流（用时15分钟）‎ ‎5.小组汇报交流 对于二次函数y=x2的图象，‎ ‎(1)你能描述图象的形状吗?与同伴进行交流．‎ ‎(2)图象与x轴有交点吗?如果有，交点坐标是什么?‎ ‎(3)当x<0时，随着x值的增大，y的值如何变化?当x>0时呢?‎ ‎(4)当x取什么值时，y的值最小?最小值是什么?你是如何知道的?‎ ‎(5)图象是轴对称图形吗?如果是，它的对称轴是什么?请你找出几对对称点，并与同伴进行交流．‎ ‎6.教师精讲点拨：二次函数y=x2的图象是抛物线.‎ ‎（1）抛物线的开口向上；‎ ‎（2）它的图象有最低点，最低点的坐标是（0，0）；‎ ‎（3）它是轴对称图形，对称轴是y轴。在对称轴左侧，y随x的增大而减少；在对称轴右侧 y随x的增大而增大。‎ ‎（4）图象与x轴有交点，这个交点也是对称轴与抛物线的交点，称为抛物线的顶点，同时也是图象的最低点，坐标为（0，0）；‎ ‎（5）因为图像有最低点，所以函数有最小值，当x=0时，y最小＝0.‎ 做一做 二次函数的图象y=-x²是什么形状?先想一想,然后作出它的图象.它与二次函数y=x²的图象有什么关系?与同伴交流。‎ 分析并总结：二次函数y=-x2的图象是抛物线. [来源:学|科|网Z|X|X|K]‎ ‎（1）抛物线的开口向下；‎ ‎（2）它的图象有最高点，最高点的坐标是（0，0）；‎ ‎（3）它是轴对称图形，对称轴是y轴。在对称轴左侧，y随x的增大而增大；在对称轴右侧，y随x的增大而减小。‎ ‎（4）图象与x轴有交点，这个交点也是对称轴与抛物线的交点，称为抛物线的顶点，同时也是图象的最高点，坐标为（0，0）；‎ ‎（5）因为图像有最高点，所以函数有最大值，当x=0时，y最大＝0. 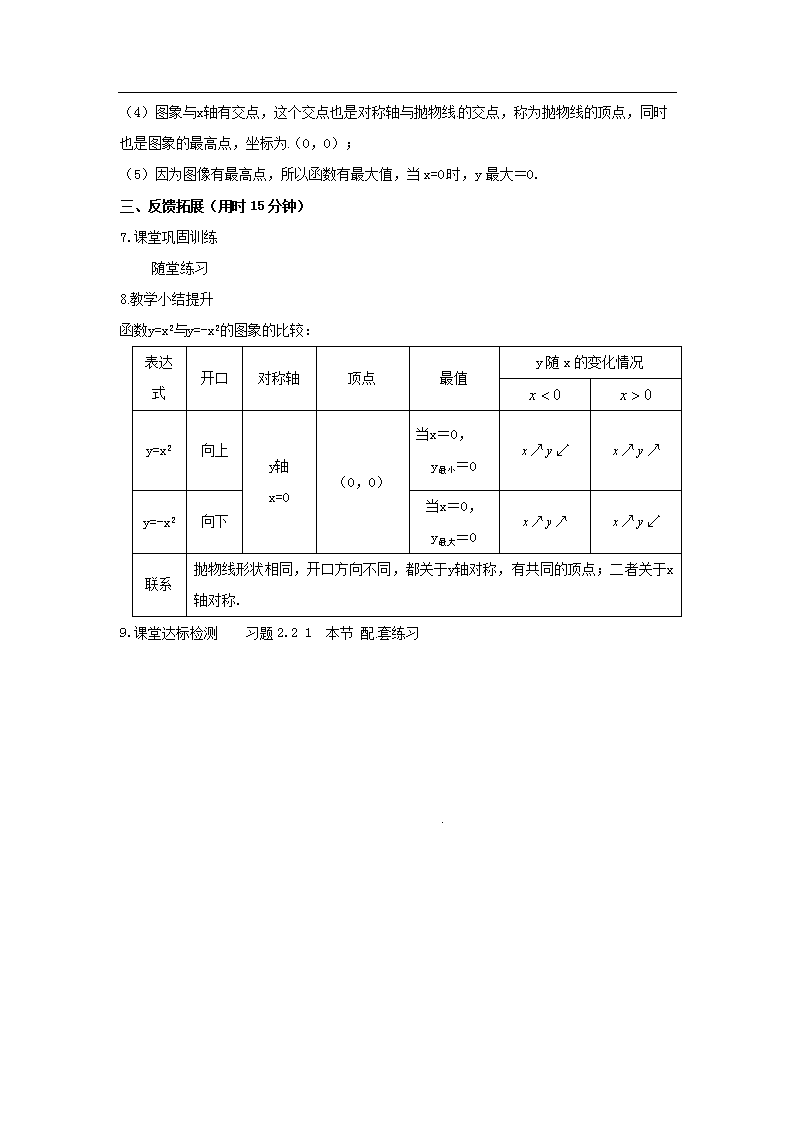‎ 三、反馈拓展（用时15分钟）‎ ‎7.课堂巩固训练 随堂练习 ‎8.教学小结提升 函数y=x2与y=-x2的图象的比较：‎ 表达式 开口 对称轴 顶点 最值 y随x的变化情况 y=x2‎ 向上 y轴 x=0‎ ‎（0，0）‎ 当x＝0，‎ y最小＝0‎ y=-x2‎ 向下 当x＝0，‎ y最大＝0‎ 联系 抛物线形状相同，开口方向不同，都关于y轴对称，有共同的顶点；二者关于x轴对称.‎ ‎9.课堂达标检测 习题2.2 1 本节 配套练习 ‎ ‎ ‎