初中数学竞赛辅导讲义及习题解答 第11讲 双曲线 8页

1 第十一讲 双曲线 形如 x ky  ( 0k )的函数叫做反比例函数，它的图象是由两条曲线组成的双曲线，与双 曲线相关的知识有： 1． 双曲线解析式 x ky  中的系数 k 决定图象的大致位置及 y 随 x 变化的状况． 2．双曲线图象上的点是关于原点 O 成中心对称，在 k >0 时函数的图象关于直线 xy  轴 对称；在 <0 时函数的图象关于直线 xy  轴对称． 3．自变量的取值是不等于零的全体实数，双曲线向坐标轴无限延伸但不能接近坐标轴． 【例题求解】 【例 1】 已知反比例函数 x ky  的图象与直线 xy 2 和 1 xy 过同一点，则当 0x 时，这 个反比例函数的函数值 y 随 的增大而 (填增大或减小)． 思路点拨 确定 k 的值，只需求出双曲线上一点的坐标即可． 注：(1)解与反比函数相关问题时，充分考虑它的对称性(关于原点 O 中心称，关于 xy  轴 对称)，这样既能从整上思考问题，又能提高思维的周密性． (2)一个常用命题： 如图，设点 A 是反比例函数 ( 0k )的图象上一点，过 A 作 AB⊥ 轴于 B，过 A 作 AC⊥ 轴于 C，则 ①S△AOB= k2 1 ； ②S 矩形 OBAC= k ． 【例 2】 如图，正比例函数 kxy  ( 0k )与反比例函数 xy 1 的图象相交于 A、C 两点，过 A 作 AB⊥ x 轴于 B，连结 BC，若 S△ABC 的面积为 S，则( ) A．S=1 B．S =2 C．S= D．S= 2k 2 思路点拨 运用双曲线的对称性，导出 S△AOB 与 S△OBC 的关系． 【例 3】 如图，已知一次函数 8 xy 和反比例函数 x ky  ( 0k )的图象在第一象限内有 两个不同的公共点 A、B． (1)求实数 k 的取值范围； (2)若△AOB 面积 S＝24，求 的值． (2003 年荆门市中考题) 思路点拨 (1)两图象有两个不同的公共点，即联立方程组有两组不同实数解； (2)S△AOB= S△COB S- S△COA，建立 的方程． 【例 4】 如图，直线 22 1  xy 分别交 x 、 y 轴于点 A、C，P 是该直线上在第一象限内的 一点，PB⊥ x 轴于 B，S△ABP=9． (1)求点 P 的坐标； (2)设点 R 与点 P 在同一个反比例函数的图象上，且点 R 在直线 PB 的右侧，作 PT⊥ 轴于 F，当△BRT 与△AOC 相似时，求点 R 的坐标． 思路点拨 (1)从已知的面积等式出发，列方程求 P 点坐标；(2)以三角形相似为条件，结合 线段长与坐标的关系求 R 坐标，但要注意分类讨论． 【例 5】 如图，正方形 OABC 的面积为 9，点 O 为坐标原点，点 A 在 轴上，点 C 在 轴 上， 点 B 在函数 x ky  ( 0k ， 0x )的图象上，点 P( m ， n )是函数 ( 0k ， 0x ) 3 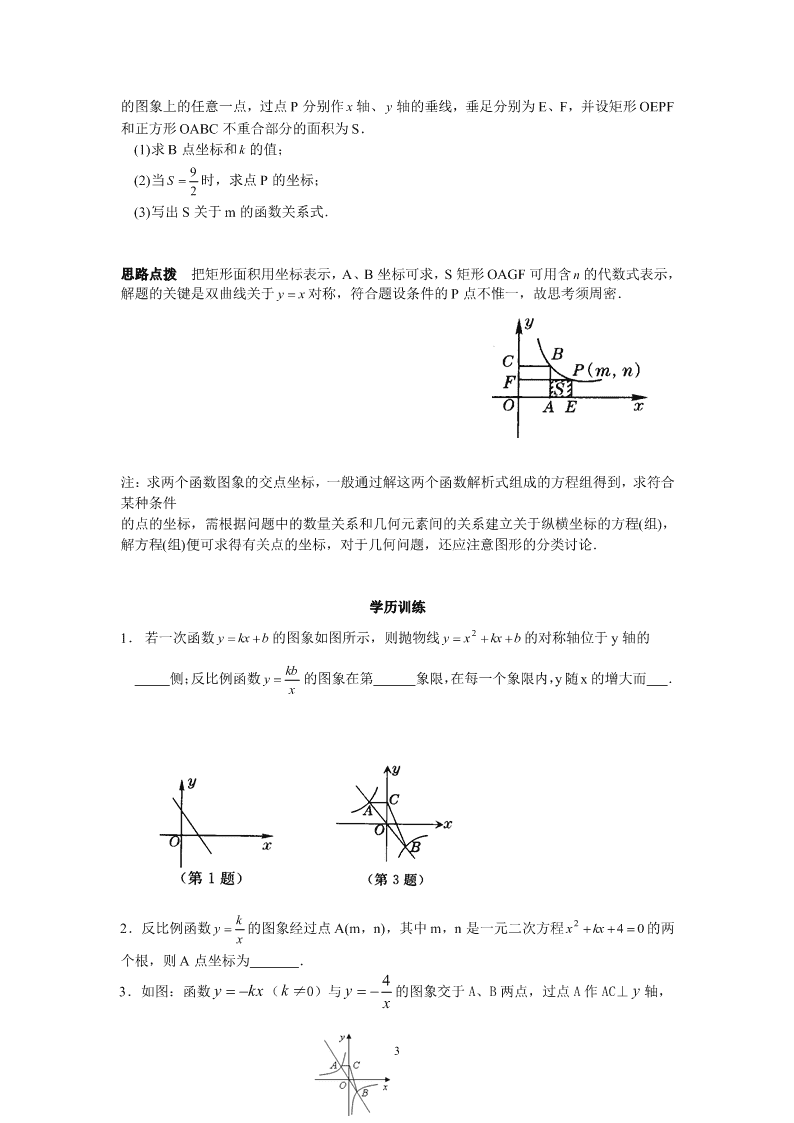的图象上的任意一点，过点 P 分别作 x 轴、 y 轴的垂线，垂足分别为 E、F，并设矩形 OEPF 和正方形 OABC 不重合部分的面积为 S． (1)求 B 点坐标和 k 的值； (2)当 2 9S 时，求点 P 的坐标； (3)写出 S 关于 m 的函数关系式． 思路点拨 把矩形面积用坐标表示，A、B 坐标可求，S 矩形 OAGF 可用含 n 的代数式表示， 解题的关键是双曲线关于 xy  对称，符合题设条件的 P 点不惟一，故思考须周密． 注：求两个函数图象的交点坐标，一般通过解这两个函数解析式组成的方程组得到，求符合 某种条件 的点的坐标，需根据问题中的数量关系和几何元素间的关系建立关于纵横坐标的方程(组)， 解方程(组)便可求得有关点的坐标，对于几何问题，还应注意图形的分类讨论． 学历训练 1． 若一次函数 bkxy  的图象如图所示，则抛物线 bkxxy  2 的对称轴位于 y 轴的 侧；反比例函数 x kby  的图象在第 象限，在每一个象限内，y随 x 的增大而 ． 2．反比例函数 x ky  的图象经过点 A(m，n)，其中 m，n 是一元二次方程 042  kxx 的两 个根，则 A 点坐标为 ． 3．如图：函数 kxy  （ k ≠0）与 xy 4 的图象交于 A、B 两点，过点 A 作 AC⊥ y 轴， 4 垂足为点 C，则△BOC 的面积为 ． 4．已知，点 P(n，2n)是第一象限的点，下面四个命题： (1)点 P 关于 y 轴对称的点 P1 的坐标是(n，-2n)； (2)点 P 到原点 O 的距离是 5 n；(3)直 线 y=-nx+2n 不经过第三象限；(4)对于函数 y= n x ，当 x＜0 时,y 随 x 的增大而减小；其中 真命题是 .(填上所有真命题的序号) 5．已知反比例函数 y= 1 m x  的图像上两点 A(x1，y1)、B（x2，y2），当 x1＜0＜x2 时，有 y1 ＜y2 ,则 m 的取值范围是( ) A．m＜O B．m＞0 C. m＜ 1 2 D.m＞ 6．已知反比例函数 x ky  的图象如图所示，则二次函数 222 kxkxy  的图象大致为( ) 7．已知反比例函数 ),0(  kx ky 当 0x 时，y 随 x 的增大面增大，那么一次函数 kkxy  的图象经过( ) A．第一、二、三象限 B．第一、二、四象限 C．第一、三、四象限 D．第二、三、四象限 8．如图，A、B 是函数 xy 1 的图象上的点，且 A、B 关于原点 O 对称，AC⊥ x 轴于 C， BD⊥ 轴于 D，如果四边形 ACBD 的面积为 S，那么( ) A． S＝1 B．12 D．S＝2 5 9．如图，已知一次函数 y=kx+b(k≠O)的图像与 x 轴、y 轴分别交于 A、B 两点，且与反比例 函数 y= x m (m≠0)的图像在第一象限交于 C 点，CD 垂直于 x 轴，垂足为 D．若 OA=OB=OD=l． （1）求点 A、B、D 的坐标； （2）求一次函数和反比例函数的解析式． 10．已知 A(x1、y1)，B(x2，y2)是直线 2 xy 与双曲线 x ky  ( 0k )的两个不同交点． (1)求 k 的取值范围； (2)是否存在这样 k 的值，使得 2 1 1 2 21 )2)(2( x x x xxx  ?若存在，求出这样的 值；若不存 在，请说明理由． 11．已知反比例函数 2 ky x 和一次函数 y＝2x-1，其中一次函数图像经过(a，b)，(a+1，b+k) 两点． (1)求反比例函数的解析式； (2)如图，已知点 A 在第一象限，且同时在上述两个函数的图像上，求 A 点坐标； (3)利用(2)的结果，请问：在 x 轴上是否存在点 P，使Δ AOP 为等腰三角形？若存在，把符 合条件的 P 点坐标都求出来；若不存在，请说明理由. 12．反比例函数 x ky  的图象上有一点 P(m，n)，其中 m、n 是关于 t 的一元二次方程 032  ktt 的两根，且 P 到原点 O 的距离为 13 ，则该反比例函数的解析式为 ． 13．如图，正比例函数 xy 3 的图象与反比例函数 ( 0k )的图象交于点 A，若 取 1， 2，3…20，对应的 Rt△AOB 的面积分别为 S1，S2，…，S20，则 S1+S2+…+S20= ． 6 14．老师给出一个函数 y=f(x)，甲、乙、丙、丁四位同学各指出这个函数的一个性质： 甲：函数图像不经过第三象限； 乙：函数图像经过第一象限； 丙：当 x＜2 时，y 随 x 的增大而减小； 丁：当 x＜2 时，y＞0 已知这四位同学叙述都正确，请构造出满足上述所有性质的一个．．函数： ． 15．已知反比例函数 xy 12 的图象和一次函数 7 kxy 的图象都经过点 P(m，2)． (1)求这个一次函数的解析式； (2)如果等腰梯形 ABCD 的顶点 A、B 在这个一次函数的图象上，顶点 C、D 在这个反 比例函数的图象上，两底 AD、BC 与 y 轴平行，且 A、B 的横坐标分别为 a 和 2a ， 求 a 的值． 16．如图，直线经过 A(1，0)，B(0，1)两点，点 P 是双曲线 xy 2 1 ( 0x )上任意一点，PM ⊥ x 轴，PN⊥ 轴，垂足分别为 M，N．PM 与直线 AB 交于点 E，PN 的延长线与直线 AB 交于点 F． (1) 求证：AF×BE＝1； (2)若平行于 AB 的直线与双曲线只有一个公共点，求公共点的坐标． (2003 年江汉油田中考题) 17．已知矩形 ABCD 的面积为 36，以此矩形的对称轴为坐标轴建立平面直角坐标系．．．．．．．．．．．．．．．．．．．．．，设点 A 的坐标为(x，y)，其中 x>0，y>0． (1)求出 y 与 x 之间的函数关系式，求出自变量 x 的取值范围； (2)用 x、y 表示矩形 ABCD 的外接圆的面积 S，并用下列方法，解答后面的问题： 方法：∵ 2 22 2 ( ) 2kka a kaa    (k 为常数且 k>0，a≠0)，且 2( ) 0ka a ∴． 2 2 2 2kaka． ∴当 ka a =0，即 ak 时， 2 2 2 ka a 取得最小值 2k． 问题：当点 A 在何位置时，矩形 ABCD 的外接圆面积 S 最小?并求出 S 的最小值； (3)如果直线 y=mx+2(m<0)与 x 轴交于点 P，与 y 轴交于点 Q，那么是否存在这样的实 数 m，使得点 P、Q 与(2)中求出的点 A 构成△PAQ 的面积是矩形 ABCD 面积的 1 6 ?若存在， 请求出 m 的值；若不存在，请说明理由． 7 参考答案 8