2021年中考数学专题复习 专题45 待定系数法（教师版含解析） 24页

专题 45 待定系数法 1.待定系数法的含义 一种求未知数的方法。将一个多项式表示成另一种含有待定系数的新的形式，这样就得到一个恒等式。 然后根据恒等式的性质得出系数应满足的方程或方程组，其后通过解方程或方程组便可求出待定的系数， 或找出某些系数所满足的关系式，这种解决问题的方法叫做待定系数法。 2. 待定系数法的应用 (1)分解因式 待定系数法是初中数学的一个重要方法。用待定系数法分解因式，就是先按已知条件把原式假设成若 干个因式的连乘积，这些因式中的系数可先用字母表示，它们的值是待定的，由于这些因式的连乘积与原 式恒等，然后根据恒等原理，建立待定系数的方程组，最后解方程组即可求出待定系数的值。在初中竞赛 中经常出现。 a.确定所求问题含待定系数的解析式。 b.根据恒等条件，列出一组含待定系数的方程。 c.解方程或消去待定系数，从而使问题得到解决。 (2)求函数解析式 初中阶段主要有正比例函数、反比例函数、一次函数、二次函数这几类函数，前面三种分别可设 y=kx， y=k/x，y=kx+b 的形式(其中 k、b 为待定系数，且 k≠0)．而二次函数可以根据题目所给条件的不同，设成 y=ax2+bx+c(a、b、c 为待定系数)，y=a (x－h) 2+k(a、k、h 为待定系数)，y=a (x－x1)(x－x2)( a、x1、x2 为待定系数)三类形式．根据题意(可以是语句形式，也可以是图象形式)，确定出 h、k、a、c、b、x1、x2 等待定系数．一般步骤如下： a.写出函数解析式的一般式，其中包括未知的系数； b.把自变量与函数的对应值代入函数解析式中，得到关于待定系数的方程或方程组。 c.解方程(组)求出待定系数的值，从而写出函数解析式。 (3)解方程 例如：已知一元二次方程的两根为 x1、x2，求二次项系数为 1 的一元二次方程时，可设该方程为 x2+mx+n=0， 则有(x－x1)(x－x2)=0，即 x2－(x1+x2)x+x1x2=0，对应相同项的系数得 m=－(x1+x2)，n=x1x2，所以所求方程为： x2－(x1+x2)x+x1x2=0． (4)分式展开 首先用未知数表示化为部分分式和的形式，展开后，根据分子、分母的多项式分别相等可列出含有未 知数的方程组，解方程组，带入所设的部分和可得结果。也可以用代值法求系数。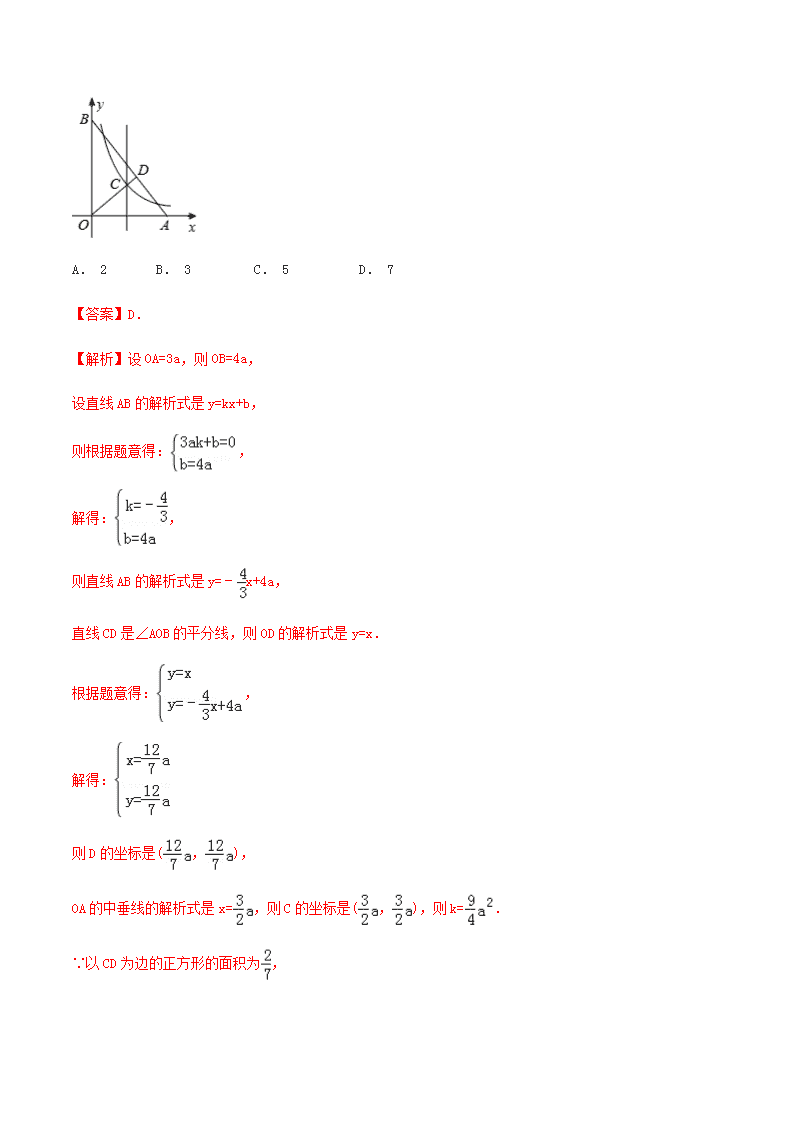 【例题 1】(2020•上海)已知反比例函数的图象经过点(2，﹣4)，那么这个反比例函数的解析式是( ) A．y B．y C．y D．y 【答案】D 【分析】已知函数图象上一点的坐标求反比例函数解析式，可先设出解析式 y ，再将点的坐标代入求出 待定系数 k 的值，从而得出答案． 【解析】设反比例函数解析式为 y ， 将(2，﹣4)代入，得：﹣4 ， 解得 k＝﹣8， 所以这个反比例函数解析式为 y ， 【对点练习】(2020 乌鲁木齐模拟)如图，在直角坐标系 xOy 中，点 A，B 分别在 x 轴和 y 轴， = ．∠AOB 的角平分线与 OA 的垂直平分线交于点 C，与 AB 交于点 D，反比例函数 y= 的图象过点 C．当以 CD 为边的正 方形的面积为 时，k 的值是( ) A． 2 B． 3 C． 5 D． 7 【答案】D． 【解析】设 OA=3a，则 OB=4a， 设直线 AB 的解析式是 y=kx+b， 则根据题意得： ， 解得： ， 则直线 AB 的解析式是 y=﹣ x+4a， 直线 CD 是∠AOB 的平分线，则 OD 的解析式是 y=x． 根据题意得： ， 解得： 则 D 的坐标是( ， )， OA 的中垂线的解析式是 x= ，则 C 的坐标是( ， )，则 k= ． ∵以 CD 为边的正方形的面积为 ， ∴2( ﹣ )2= ， 则 a2= ， ∴k= × =7． 【点拨】本题考查了待定系数法求函数解析式，正确求得 C 和 D 的坐标是解决本题的关键． 设 OA=3a，则 OB=4a，利用待定系数法即可求得直线 AB 的解析式，直线 CD 的解析式是 y=x，OA 的中垂线的 解析式是 x= ，解方程组即可求得 C 和 D 的坐标，根据以 CD 为边的正方形的面积为 ，即 CD2= ，据此即 可列方程求得 a2 的值，则 k 即可求解． 【例题 2】(2020•遂宁)如图，在平面直角坐标系中，已知点 A 的坐标为(0，2)，点 B 的坐标为(1，0)，连 结 AB，以 AB 为边在第一象限内作正方形 ABCD，直线 BD 交双曲线 y═ (k≠0)于 D、E 两点，连结 CE，交 x 轴于点 F． (1)求双曲线 y (k≠0)和直线 DE 的解析式． (2)求△DEC 的面积． 【答案】见解析。 【分析】(1)作 DM⊥y 轴于 M，通过证得△AOB≌△DMA(AAS)，求得 D 的坐标，然后根据待定系数法即可求得 双曲线 y (k≠0)和直线 DE 的解析式． (2)解析式联立求得 E 的坐标，然后根据勾股定理求得 DE 和 DB，进而求得 CN 的长，即可根据三角形面积公 式求得△DEC 的面积． 【解析】∵点 A 的坐标为(0，2)，点 B 的坐标为(1，0)， ∴OA＝2，OB＝1， 作 DM⊥y 轴于 M， ∵四边形 ABCD 是正方形， ∴∠BAD＝90°，AB＝AD， ∴∠OAB+∠DAM＝90°， ∵∠OAB+∠ABO＝90°， ∴∠DAM＝∠ABO， 在△AOB 和△DMA 中 ∠ th ∠ h∠ ht ∠ h 砀晦 ° t ， ∴△AOB≌△DMA(AAS)， ∴AM＝OB＝1，DM＝OA＝2， ∴D(2，3)， ∵双曲线 y═ (k≠0)经过 D 点， ∴k＝2×3＝6， ∴双曲线为 y ， 设直线 DE 的解析式为 y＝mx+n， 把 B(1，0)，D(2，3)代入得 ൅ 晦 ൅ 耀 ，解得 耀 耀 ， ∴直线 DE 的解析式为 y＝3x﹣3； (2)连接 AC，交 BD 于 N， ∵四边形 ABCD 是正方形， ∴BD 垂直平分 AC，AC＝BD， 解 耀 耀 得 耀 或 ⸷ ， ∴E(﹣1，﹣6)， ∵B(1，0)，D(2，3)， ∴DE ൅ ⸷ ൅ 耀 ൅ 3 ⸷晦 ，DB ⸷ ൅ 耀 ⸷晦 ， ∴CN ⸷ BD ⸷晦 ， ∴S△DEC ⸷ DE•CN ⸷ × 耀 ⸷晦 × ⸷晦 ⸷ ． 【对点练习】(2019 湖北黄冈)如图①，在平面直角坐标系 xOy 中，已知 A(﹣2，2)，B(﹣2，0)，C(0，2)， D(2，0)四点，动点 M 以每秒 个单位长度的速度沿 B→C→D 运动(M 不与点 B、点 D 重合)，设运动时间为 t(秒)． (1)求经过 A、C、D 三点的抛物线的解析式； (2)点 P 在(1)中的抛物线上，当 M 为 BC 的中点时，若△PAM≌△PBM，求点 P 的坐标； (3)当 M 在 CD 上运动时，如图②．过点 M 作 MF⊥x 轴，垂足为 F，ME⊥AB，垂足为 E．设矩形 MEBF 与△BCD 重叠部分的面积为 S，求 S 与 t 的函数关系式，并求出 S 的最大值； (4)点 Q 为 x 轴上一点，直线 AQ 与直线 BC 交于点 H，与 y 轴交于点 K．是否存在点 Q，使得△HOK 为等腰三 角形？若存在，直接写出符合条件的所有 Q 点的坐标；若不存在，请说明理由． 【答案】见解析。 【解析】(1)设函数解析式为 y＝ax2+bx+c， 将点 A(﹣2，2)，C(0，2)，D(2，0)代入解析式可得 ， ∴ ， ∴y＝﹣ ﹣ x+2； (2)∵△PAM≌△PBM， ∴PA＝PB，MA＝MB， ∴点 P 为 AB 的垂直平分线与抛物线的交点， ∵AB＝2， ∴点 P 的纵坐标是 1， ∴1＝﹣ ﹣ x+2， ∴x＝﹣1+ 或 x＝﹣1﹣ ， ∴P(﹣1﹣ ，1)或 P(﹣1+ ，1)； (3)CM＝ t﹣2 ，MG＝ CM＝2t﹣4， MD＝4 ﹣(BC+CM)＝4 ﹣(2 + t﹣2 )＝4 ﹣ t， MF＝ MD＝4﹣t， ∴BF＝4﹣4+t＝t， ∴S＝ (GM+BF)×MF＝ (2t﹣4+t)×(4﹣t)＝﹣ +8t﹣8＝﹣ (t﹣ )2+ ； 当 t＝ 时，S 最大值为 ； (3)设点 Q(m，0)，直线 BC 的解析式 y＝﹣x+2， 直线 AQ 的解析式 y＝﹣ (x+2)+2， ∴K(0， )，H( ， )， ∴OK2＝ ，OH2＝ + ，HK2＝ + ， ①当 OK＝OH 时， ＝ + ， ∴m2﹣4m﹣8＝0， ∴m＝2+2 或 m＝2﹣2 ； ②当 OH＝HK 时， + ＝ + ， ∴m2﹣8＝0， ∴m＝2 或 m＝﹣2 ； ③当 OK＝HK 时， ＝ + ，不成立； 综上所述：Q(2+2 ，0)或 Q(2﹣2 ，0)或 Q(2 ，0)或 Q(﹣2 ，0)； 【点拨】本题考查二次函数综合；熟练应用待定系数法求函数解析式，掌握三角形全等的性质，直线交 点的求法是解题的关键． 一、选择题 1.(2020•乐山)直线 y＝kx+b 在平面直角坐标系中的位置如图所示，则不等式 kx+b≤2 的解集是( ) A．x≤﹣2 B．x≤﹣4 C．x≥﹣2 D．x≥﹣4 【答案】C 【分析】根据待定系数法求得直线的解析式，然后求得函数 y＝2 时的自变量的值，根据图象即可求得． 【解析】∵直线 y＝kx+b 与 x 轴交于点(2，0)，与 y 轴交于点(0，1)， ∴ ൅ l 晦 l ⸷ ，解得 ⸷ l ⸷∴直线为 y ⸷ ൅ 1， 当 y＝2 时，2 ⸷ ൅ 1，解得 x＝﹣2， 由图象可知：不等式 kx+b≤2 的解集是 x≥﹣2 2．(2019 桂林)如图，四边形 ABCD 的顶点坐标分别为 A(﹣4，0)，B(﹣2，﹣1)，C(3，0)，D(0，3)，当过 点 B 的直线 l 将四边形 ABCD 分成面积相等的两部分时，直线 l 所表示的函数表达式为( ) A．y＝ x+ B．y＝ x+ C．y＝x+1 D．y＝ x+ 【答案】D． 【解析】由 A(﹣4，0)，B(﹣2，﹣1)，C(3，0)，D(0，3)， ∴AC＝7，DO＝3， ∴四边形 ABCD 分成面积＝ AC×(|yB|+3)＝ ＝14， 可求 CD 的直线解析式为 y＝﹣x+3， 设过 B 的直线 l 为 y＝kx+b， 将点 B 代入解析式得 y＝kx+2k﹣1， ∴直线 CD 与该直线的交点为( ， )， 直线 y＝kx+2k﹣1 与 x 轴的交点为( ，0)， ∴7＝ ×(3﹣ )×( +1)， ∴k＝ 或 k＝0， ∴k＝ ， ∴直线解析式为 y＝ x+ 3．明君社区有一块空地需要绿化，某绿化组承担了此项任务，绿化组工作一段时间后，提高了工作效率．该 绿化组完成的绿化面积 S(单位：m2)与工作时间 t(单位：h)之间的函数关系如图所示，则该绿化组提高工作 效率前每小时完成的绿化面积是( ) A．300m2 B．150m2 C．330m2 D．450m2 【答案】B 【解析】根据待定系数法可求直线 AB 的解析式，再根据函数上点的坐标特征得出当 x=2 时，y 的值，再根 据工作效率=工作总量÷工作时间，列出算式求出该绿化组提高工作效率前每小时完成的绿化面积．如图， 设直线 AB 的解析式为 y=kx+b，则 ， 解得 ． 故直线 AB 的解析式为 y=450x﹣600， 当 x=2 时，y=450×2﹣600=300， 300÷2=150(m2)． 答：该绿化组提高工作效率前每小时完成的绿化面积是 150m2． 4. 已知关于 x 的分式方程 ＝1 的解是非正数，则 a 的取值范围是( ) A.a≤－1 B.a≤－1，且 a≠－2 C.a≤1，且 a≠－2 D.a≤1 【解析】去分母，得 a＋2＝x＋1， 解得 x＝a＋1． ∵x≤0．且 x＋1≠0， ∴a＋1≤0，且 a＋1≠－1， ∴a≤－1，且 a≠－2， ∴a≤－1，且 a≠2．故选 B． 5.(2019•浙江绍兴)若三点(1，4)，(2，7)，(a，10)在同一直线上，则 a 的值等于( ) A．﹣1 B．0 C．3 D．4 【答案】C． 【解析】设经过(1，4)，(2，7)两点的直线解析式为 y＝kx+b， ∴ ∴ ， ∴y＝3x+1， 将点(a，10)代入解析式，则 a＝3 二、填空题 6.(2020 年浙江金华模拟)如图，在平面直角坐标系中，菱形 OBCD 的边 OB 在 x 轴正半轴上，反比例函数 ky (x 0)x   的图象经过该菱形对角线的交点 A，且与边 BC 交于点 F. 若点 D 的坐标为(6，8)，则点 F 的坐 标是 【答案】 812 3      ， . 【解析】反比例函数综合题；曲线上点的坐标与方程的关系；待定系数法的应用；菱形的性质；中点坐标； 方程思想的应用. ∵菱形 OBCD 的边 OB 在 x 轴正半轴上，点 D 的坐标为(6，8)， ∴ 2 2OD DC OD 6 8 10     .∴点 B 的坐标为(10，0)，点 C 的坐标为(16，8). ∵菱形的对角线的交点为点 A，∴点 A 的坐标为(8，4). ∵反比例函数 ky (x 0)x   的图象经过点 A，∴ k 8 4 32   . ∴反比例函数为 32y x  . 设直线 BC 的解析式为 y mx n  ，∴ 4m16m n 8 3 10m n 0 40n 3          . 7.若一个二次函数的二次项系数为－1，且图象的顶点坐标为(0,－3).则这个二次函数的表达式为________． 【答案】y=﹣x2﹣3 【解析】∵抛物线二次项系数为-1，顶点坐标为(0，-3)， ∴抛物线的顶点式为 y=-(x－0)2-3, 即 y=-x2-3 故答案为：y=-x2-3。 三、解答题 8．(2020•苏州)某商店代理销售一种水果，六月份的销售利润 y(元)与销售量 x(kg)之间函数关系的图象如 图中折线所示．请你根据图象及这种水果的相关销售记录提供的信息，解答下列问题： (1)截止到 6 月 9 日，该商店销售这种水果一共获利多少元？ (2)求图象中线段 BC 所在直线对应的函数表达式． 日期 销售记录 6 月 1 日 库存 600kg，成本价 8 元/kg，售价 10 元/kg(除了促销降价，其他时间售价 保持不变)． 6 月 9 日 从 6 月 1 日至今，一共售出 200kg． 6 月 10、11 日 这两天以成本价促销，之后售价恢复到 10 元/kg． 6 月 12 日 补充进货 200kg，成本价 8.5 元/kg． 6 月 30 日 800kg 水果全部售完，一共获利 1200 元． 【答案】见解析。 【分析】(1)由表格信息可知，从 6 月 1 日到 6 月 9 日，成本价 8 元/kg，售价 10 元/kg，一共售出 200kg， 根据利润＝每千克的利润×销售量列式计算即可； (2)设 B 点坐标为(a，400)，根据题意列方程求出点 B 的坐标，设线段 BC 所在直线对应的函数表达式为 y＝kx+b，利用待定系数法解答即可． 【解析】(1)200×(10﹣8)＝400(元) 答：截止到 6 月 9 日，该商店销售这种水果一共获利 400 元； (2)设点 B 坐标为(a，400)，根据题意得： (10﹣8)×(600﹣a)+(10﹣8.5)×200＝1200﹣400， 解这个方程，得 a＝350， ∴点 B 坐标为(350，400)， 设线段 BC 所在直线对应的函数表达式为 y＝kx+b，则： 耀晦 ൅ l ൅晦晦 晦晦 ൅ l ⸷晦晦 ，解得 ⸷ 砀 l 晦晦晦 砀 ， ∴线段 BC 所在直线对应的函数表达式为 ⸷ 砀 晦晦晦 砀 ． 9．(2020•陕西)某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术．这种瓜苗早期在农科所的 温室中生长，长到大约 20cm 时，移至该村的大棚内，沿插杆继续向上生长．研究表明，60 天内，这种瓜苗 生长的高度 y(cm)与生长时间 x(天)之间的关系大致如图所示． (1)求 y 与 x 之间的函数关系式； (2)当这种瓜苗长到大约 80cm 时，开始开花结果，试求这种瓜苗移至大棚后．继续生长大约多少天，开始 开花结果？ 【分析】(1)分段函数，利用待定系数法解答即可； (2)利用(1)的结论，把 y＝80 代入求出 x 的值即可解答． 【解析】(1)当 0≤x≤15 时，设 y＝kx(k≠0)， 则：20＝15k， 解得 k ൅ 耀 ， ∴y ൅ 耀 ； 当 15＜x≤60 时，设 y＝k′x+b(k≠0)， 则： 晦 ⸷ ൅ l ⸷͹晦 晦 ൅ l ， 解得 ⸷晦 耀 l 耀晦 ， ∴y ⸷晦 耀 耀晦 ， ∴ ൅ 耀 晦 ⸷ ⸷晦 耀 耀晦⸷ ＜ 晦 ； (2)当 y＝80 时，80 ⸷晦 耀 耀晦 ，解得 x＝33， 33﹣15＝18(天)， ∴这种瓜苗移至大棚后．继续生长大约 18 天，开始开花结果． 10．(2020•河北)表格中的两组对应值满足一次函数 y＝kx+b，现画出了它的图象为直线 1，如图．而某同 学为观察 k，b 对图象的影响，将上面函数中的 k 与 b 交换位置后得另一个一次函数，设其图象为直线 l'． x ﹣1 0 y ﹣2 1 (1)求直线 1 的解析式； (2)请在图上画出直线 l'(不要求列表计算)，并求直线 l'被直线 l 和 y 轴所截线段的长； (3)设直线 y＝a 与直线 1，l′及 y 轴有三个不同的交点，且其中两点关于第三点对称，直接写出 a 的值． 【分析】(1)根据待定系数法求得即可； (2)画出直线 l，求得两直线的交点，根据勾股定理即可求得直线 l'被直线 l 和 y 轴所截线段的长； (3)求得两条直线与直线 y＝a 的交点横坐标，分三种情况讨论求得即可． 【解析】(1)∵直线 l′：y＝bx+k 中，当 x＝﹣1 时，y＝﹣2；当 x＝0 时，y＝1， ∴ l ൅ ⸷ ，解得 ⸷ l 耀 ， ∴直线 1′的解析式为 y＝3x+1； ∴直线 1 的解析式为 y＝x+3； (2)如图，解 ൅ 耀 耀 ൅ ⸷ 得 ⸷ ൅ ， ∴两直线的交点为(1，4)， ∵直线 1′：y＝3x+1 与 y 轴的交点为(0，1)， ∴直线 l'被直线 l 和 y 轴所截线段的长为： ⸷ ൅ ൅ ⸷ ⸷晦 ； (3)把 y＝a 代入 y＝3x+1 得，a＝3x+1，解得 x ⸷ 耀 ； 把 y＝a 代入 y＝x+3 得，a＝x+3，解得 x＝a﹣3； 当 a﹣3 ൅ ⸷ 耀 0 时，a ， 当 ⸷ (a﹣3+0) ⸷ 耀 时，a＝7， 当 ⸷ ⸷ 耀 ൅ 0)＝a﹣3 时，a ⸷͹ ， ∴直线 y＝a 与直线 1，l′及 y 轴有三个不同的交点，且其中两点关于第三点对称，则 a 的值为 或 7 或 ⸷͹ ． 11.已知： ，求 A、B、C 的值。 【答案】A＝ 、B＝ 、C＝ ． 【解析】去分母，得 x2－x＋2＝ A(x－3)(x＋2)＋Bx(x＋2)＋Cx(x－3)． 根据恒等式定义，选择 x 的适当特定值，带入恒等式可直接求出 A，B，C 的值， 当 x＝0 时，有 2＝－6A，得 A＝ ； 当 x＝3 时，有 8＝15B，得 B＝ ； 当 x＝－2 时，有 8＝10C，得 C＝ ． 12．〔2020 上海模拟〕某工厂生产一种产品，当生产数量至少为 10 吨，但不超过 50 吨时，每吨的成本 y〔万 元/吨〕与生产数量 x〔吨〕的函数关系式如下图、 〔1〕求 y 关于 x 的函数解析式，并写出它的定义域； 〔2〕当生产这种产品的总成本为 280 万元时，求该产品的生产数量。 〔注：总成本=每吨的成本×生产数量〕 【答案】(1)y=﹣x/10+11〔10≤x≤50〕 (2)该产品的生产数量为 40 吨. 【解析】〔1〕利用图象设 y 关于 x 的函数解析式为 y=kx+b， 将〔10，10〕〔50，6〕代入解析式得： 解得： y=﹣x/10+11〔10≤x≤50〕 〔2〕当生产这种产品的总成本为 280 万元时， x〔﹣x/10+11〕=280， 解得：x1=40，x2=70〔不合题意舍去〕， 故该产品的生产数量为 40 吨. 13．(2019 辽宁抚顺)如图，抛物线 y＝﹣x2+bx+c 与直线 y＝mx+n 交于 B(0，4)，C(3，1)两点．直线 y＝mx+n 与 x 轴交于点 A，P 为直线 AB 上方的抛物线上一点，连接 PB，PO． (1)求抛物线的解析式 (2)如图 1，连接 PC，OC，△OPC 和△OPB 面积之比为 1：2，求点 P 的坐标； (3)如图 2，PB 交抛物线对称轴于 M，PO 交 AB 于 N，连接 MN，PA，当 MN∥PA 时，直接写出点 P 的坐标． 【答案】见解析。 【解析】(1)直接将 B(0，4)，C(3，1)代入 y＝﹣x2+bx+c，解方程组即可； (2)待定系数法求 BC 解析式：y＝﹣x+4，OC 解析式：y＝ x，设 P(m，﹣m2+2m+4)，由△OPC 和△OPB 面积 之比为 1：2，可得：2m＝2(﹣ + m+6)，求解即可得点 P 的坐标； (3)过点 P 作 PD⊥y 轴于点 D，交抛物线对称轴于点 E，过点 N 作 NF⊥y 轴于点 F，设点 P(m，﹣m2+2m+4)， 根据相似三角形性质可得方程求解即可． 解：(1)B(0，4)，C(3，1)代入 y＝﹣x2+bx+c， 可得 b＝2，c＝4， ∴y＝﹣x2+2x+4； (2)B(0，4)，C(3，1)代入 y＝mx+n， 可得 m＝﹣1，n＝4， ∴y＝﹣x+4， 易求直线 OC 解析式为：y＝ x ∵P 为直线 AB 上方的抛物线上一点， 设 P(m，﹣m2+2m+4)，则 0＜m＜3，过点 P 作 PD⊥y 轴于 D，作 PF⊥x 轴于 F，交 OC 于 G，过 C 作 CE⊥x 轴 于 E， ∴G(m， m)，E(3，0)， ∴PD＝m，PG＝(﹣m2+2m+4)﹣ m＝﹣m2+ m+4，OE＝3 S△OBP＝ OB•PD＝2m， S△OPC＝ OE•PG＝﹣ + m+6， ∵△OPC 和△OPB 面积之比为 1：2， ∴2m＝2(﹣ + m+6)，解得：m1＝ ，m2＝ (舍去)； ∴P( ， )； (3)∵y＝﹣x2+2x+4＝﹣(x﹣1)2+5 ∴抛物线对称轴为：直线 x＝1 如图 2，过点 P 作 PD⊥y 轴于点 D，交抛物线对称轴于点 E，过点 N 作 NF⊥y 轴于点 F， 设点 P(m，﹣m2+2m+4)，则 PE＝m﹣1，DE＝1，DP＝m 易得直线 OP 解析式为：y＝ x，联立方程组 解得： ，∴FN＝ ， ∵MN∥PA ∴ ＝ ∵ME∥y 轴， ∴ ＝ ， ∵FN∥x 轴， ∴ ＝ ， ∴ ＝ ，即：DE•OA＝FN•DP，1×4＝ ×m， 解得： (舍去)， ， ∴P( ， )． 14．在平面直角坐标系 xOy 中，抛物线 y=mx2﹣2mx+m﹣1(m＞0)与 x 轴的交点为 A，B． (1)求抛物线的顶点坐标； (2)横、纵坐标都是整数的点叫做整点． ①当 m=1 时，求线段 AB 上整点的个数； ②若抛物线在点 A，B 之间的部分与线段 AB 所围成的区域内(包括边界)恰有 6 个整点，结合函数的图象， 求 m 的取值范围． 【答案】见解析。 【解析】(1)∵y=mx2﹣2mx+m﹣1=m(x﹣1)2﹣1， ∴抛物线顶点坐标(1，﹣1)． (2)①∵m=1， ∴抛物线为 y=x2﹣2x， 令 y=0，得 x=0 或 2，不妨设 A(0，0)，B(2，0)， ∴线段 AB 上整点的个数为 3 个． ②如图所示，抛物线在点 A，B 之间的部分与线段 AB 所围成的区域内(包括边界)恰有 6 个整点， ∴点 A 在(﹣1，0)与(﹣2，0)之间(包括(﹣1，0))， 当抛物线经过(﹣1，0)时，m= ， 当抛物线经过点(﹣2，0)时，m= ， ∴m 的取值范围为 ＜m≤ ． 【点拨】本题考查抛物线与 x 轴的交点、配方法确定顶点坐标、待定系数法等知识，解题的关键是灵活运 用这些知识解决问题，属于中考常考题型．