2011初三数学二模题-昌平 6页

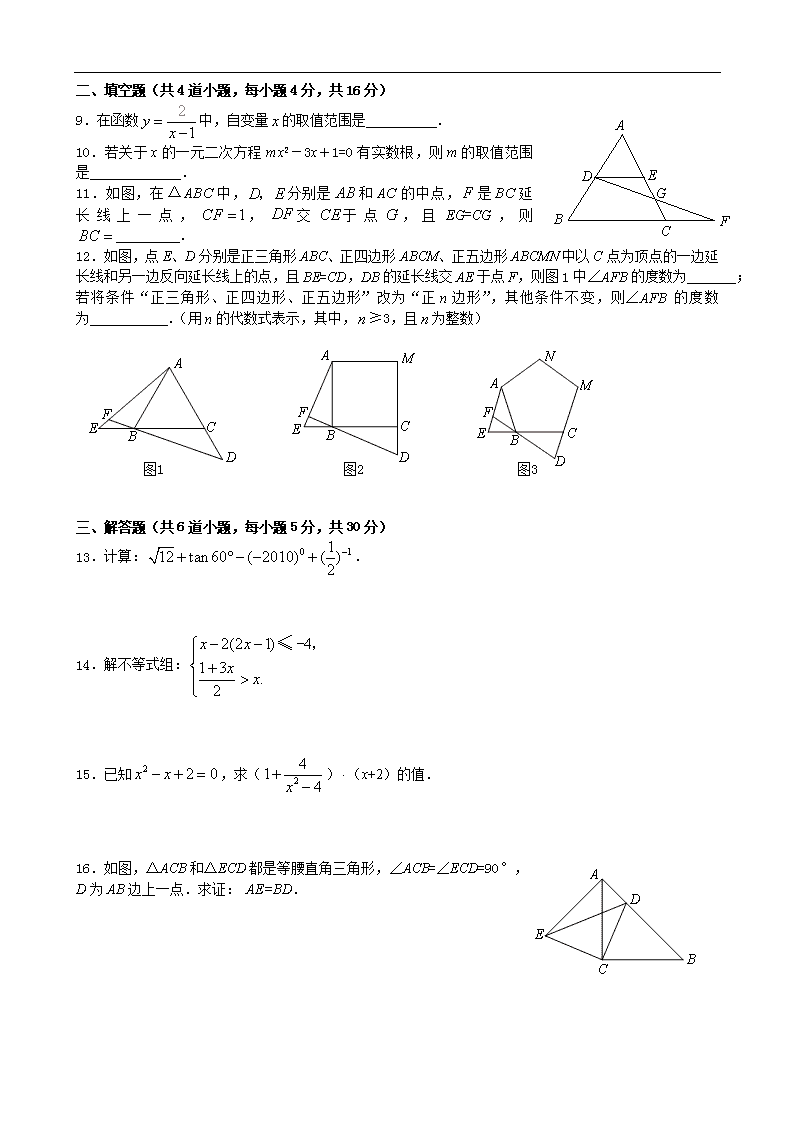
昌平区2010—2011学年第二学期初三年级第二次统一练习 ‎ 　　　 数　学　 2011．5‎ 考生须知 ‎1．本试卷共6页，共五道大题，25个小题，满分120分。考试时间120分钟。‎ ‎2．在试卷和答题卡上认真填写学校名称、姓名和考试编号。‎ ‎3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效。‎ ‎4．考试结束，请将本试卷和答题卡一并交回。‎ 一、选择题（共8道小题，每小题4分，共32分）‎ 下列各题均有四个选项，其中只有一个是符合题意的．‎ ‎1．2的绝对值是 A．2 B．2 C． D．‎ ‎2．下列运算正确的是 A． B． C． D．‎ ‎3．如图，已知直线AB∥CD，CE交AB于点F，∠DCF=110°，且AE=AF，则∠A等于 A． 　　B．　　C． D．‎ ‎4．若一个多边形的每个外角都等于，则它的边数是 Ａ．6 Ｂ．7 Ｃ．8 Ｄ．9‎ ‎5．从1、2、3、4、5、6这六个数中随机取出一个数，取出的数是3的倍数的概率是 A． B． C． D．‎ ‎6．把代数式分解因式，下列结果中正确的是 A． B． C． D．‎ ‎7．将二次函数化为的形式，结果为 A． B． C． D．‎ ‎８．下列图案给出了折叠一个直角边长为2的等腰直角三角形纸片（图1）的全过程：首先对折，如图2，折痕CD交AB于点D；打开后，过点D任意折叠，使折痕DE交BC于点E，如图3；打开后，如图4；再沿AE折叠，如图5；打开后，折痕如图6．则折痕DE和AE长度的和的最小值是 ‎ ‎ ‎ ‎ A． B．1+ C．2 D．3‎ 二、填空题（共4道小题，每小题4分，共16分）‎ A D B C F G E ‎9．在函数中，自变量的取值范围是 ．‎ ‎10．若关于x的一元二次方程m x2－3x＋1=0有实数根，则m的取值范围是 ．‎ ‎11．如图，在中，分别是和的中点，是延长线上一点，，交于点，且EG=CG，则 ．‎ ‎12．如图，点E、D分别是正三角形ABC、正四边形ABCM、正五边形ABCMN中以C点为顶点的一边延长线和另一边反向延长线上的点，且BE=CD，DB的延长线交AE于点F，则图1中∠AFB的度数为 ；若将条件“正三角形、正四边形、正五边形”改为“正n边形”，其他条件不变，则∠AFB 的度数为 ．（用n的代数式表示，其中，≥3，且为整数）‎ ‎ ‎ 三、解答题（共6道小题，每小题5分，共30分）‎ ‎13．计算：．‎ ‎14．解不等式组：‎ ‎15．已知，求（）（x+2）的值．‎ ‎16．如图，△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，‎ D为AB边上一点．求证： AE=BD．‎ l1‎ ‎17．如图，已知直线经过点和点，另一条直线 经过点，且与轴相交于点．‎ （1） 求直线的解析式；‎ ‎（2）若的面积为3，求的值．‎ ‎18．列方程（组）解应用题 某服装厂接到加工720件衣服的订单，原计划每天做48件，即可顺利交货．但还没开工，又接到客户提前5天交货的要求，所以，每天必需多加工几件衣服才能按时交货．问每天应比原计划多加工多少件衣服？‎ 四、解答题（共4道小题，每小题均5分，共20分）‎ ‎19．梯形ABCD中DC∥AB， AB =2DC，对角线AC、BD相交于点O， BD=4，过AC的中点H作EF∥BD分别交AB、AD于点E、F，求EF的长. ‎ ‎20．如图，已知点C在⊙O上，延长直径AB到点P，连接PC，∠COB=2∠PCB．‎ ‎（1）求证：PC是⊙O的切线；‎ ‎（2）若AC=PC，且PB=3，M是⊙O下半圆弧的中点，求MA的长．‎ ‎21．某中学开展了一次“诚信做人”的主题演讲比赛．赛程共分“预赛、复赛和决赛”三个阶段，预赛由各班举行，全员参加，按统一标准评分．统计后制成“预赛成绩统计图（未画完整）”，从预赛中各年级产生名选手进行复赛，成绩见“复赛成绩统计表”．（采用分制，得分都为分以上的整数．）‎ ‎300‎ ‎250‎ ‎150‎ ‎100‎ ‎50‎ ‎200‎ ‎0‎ ‎115‎ ‎60‎ ‎260‎ ‎40‎ 人数 年级 七年级 八年级 九年级 ‎61－70分 ‎71－80分 ‎81－90分 ‎91－100分 预赛成绩统计图 ‎50‎ ‎200‎ ‎180‎ ‎185‎ ‎250‎ ‎300‎ ‎100‎ 年级 ‎10名选手的复赛成绩（分）‎ 七 ‎81 85 89 81 87 99 80 76 91 86‎ 八 ‎97 88 88 87 85 87 85 85 76 77‎ 九 ‎80 81 96 80 80 97 88 79 85 89‎ 复赛成绩统计表 ‎（1）如果将九年级预赛成绩制成扇形统计图，则“分以上的人数”对应的圆心角度数是___________．‎ ‎（2）如果八年级复赛成绩在分以上的人数是预赛时同类成绩人数的，请补全预赛成绩统计图．‎ ‎（3）复赛成绩中，七年级选手的成绩的中位数是___________；九年级选手的成绩的众数是 ．‎ ‎22．如图，一个横截面为Rt△ABC的物体，∠ACB=90°，∠CAB=30°，BC=1米，师傅要把此物体搬到墙边，先将AB边放在地面（直线m上），再按顺时针方向绕点B翻转到△B的位置（B在m上），最后沿射线B的方向平移到△的位置，其平移距离为线段AC的长度（此时，恰好靠在墙边）．‎ ‎（1）直接写出AB、AC的长；‎ ‎（2）画出在搬动此物体的整个过程中A点所经过的路径，‎ 并求出该路径的长度．‎ 五、解答题（共3道小题，第23小题6分，第24，25小题各8分，共22分）‎ ‎23． 如图，在△ABC中，BC=3，AC=2，P为BC边上一个动点，过点P作PD∥AB，交AC于点D，连结BD．‎ ‎（1）如图1，若∠C=45°，请直接写出：当= 时，‎ ‎△BDP的面积最大；‎ ‎（2）如图2，若∠C=α为任意锐角，则当点P在BC上何处时，‎ ‎△BDP的面积最大？‎ ‎ ‎ ‎ ‎ ‎24．现场学习：我们知道，若锐角α的三角函数值为sinα = m，则可通过计算器得到角α的大小，这时我们用arc sin m来表示α，记作：α=arc sin m；若cos α = m，则记α = arc cos m；若tan α = m，则记α = arc tan m．‎ ‎ 解决问题：如图，已知正方形ABCD，点E是边AB上一动点，点F在AB边或其延长线上，点G在边AD上．连结ED，FG，交点为H．‎ ‎（1）如图1，若AE=BF=GD，请直接写出∠EHF= °；‎ ‎（2）如图2，若EF =CD，GD=AE，设∠EHF=α．请判断当点E在AB上运动时， ∠EHF的大小是否发生变化？若发生变化，请说明理由；若不发生变化，请求出α． ‎ ‎25.如图1，在平面直角坐标系中，等腰直角三角形OMN的斜边ON在x轴上，顶点M的坐标为（3，3），MH为斜边上的高．抛物线C：与直线及过N点垂直于x轴的直线交于点D．点P（m，0）是x轴上一动点，过点P作y轴的平行线，交射线OM与点E．设以M、E、H、N为顶点的四边形的面积为S．‎ ‎（1）直接写出点D的坐标及n的值；‎ ‎（2）判断抛物线C的顶点是否在直线OM上？并说明理由；‎ ‎（3）当m≠3时，求S与m的函数关系式；‎ ‎（4）如图2，设直线PE交射线OD于R，交抛物线C于点Q，‎ 以RQ为一边，在RQ的右侧作矩形RQFG，其中RG=，‎ 直接写出矩形RQFG与等腰直角三角形OMN重叠部分为 轴对称图形时m的取值范围．‎ ‎ ‎