2020中考数学复习基础小卷速测十一三角形相关综合 6页

基础小卷速测（十一） 三角形相关综合 一、选择题 ‎1.如图，直线a∥b，∠1=85°，∠2=35°，则∠3=（ ）‎ A．85°‎ B．60°‎ C．50°‎ D．35°‎ ‎ ‎ ‎2.若等腰三角形的腰长为10，底边长为12，则底边上的高为（ ）‎ A.6 B.7 C.8 D.9‎ ‎3．如图，梯子AB靠在墙上，梯子的底端A到墙根O的距离为2m，梯子的顶端B到地面的距离为7m，现将梯子的底端A向外移动到A′，使梯子的底端A′到墙根O的距离等于3m，同时梯子的顶端B下降至B′，则BB′（　　）‎ A．小于1m B．大于1m C．等于1m D．小于或等于1m ‎4．如图所示，线段的垂直平分线交线段于点，，则=（ ）‎ A. B. C. D. 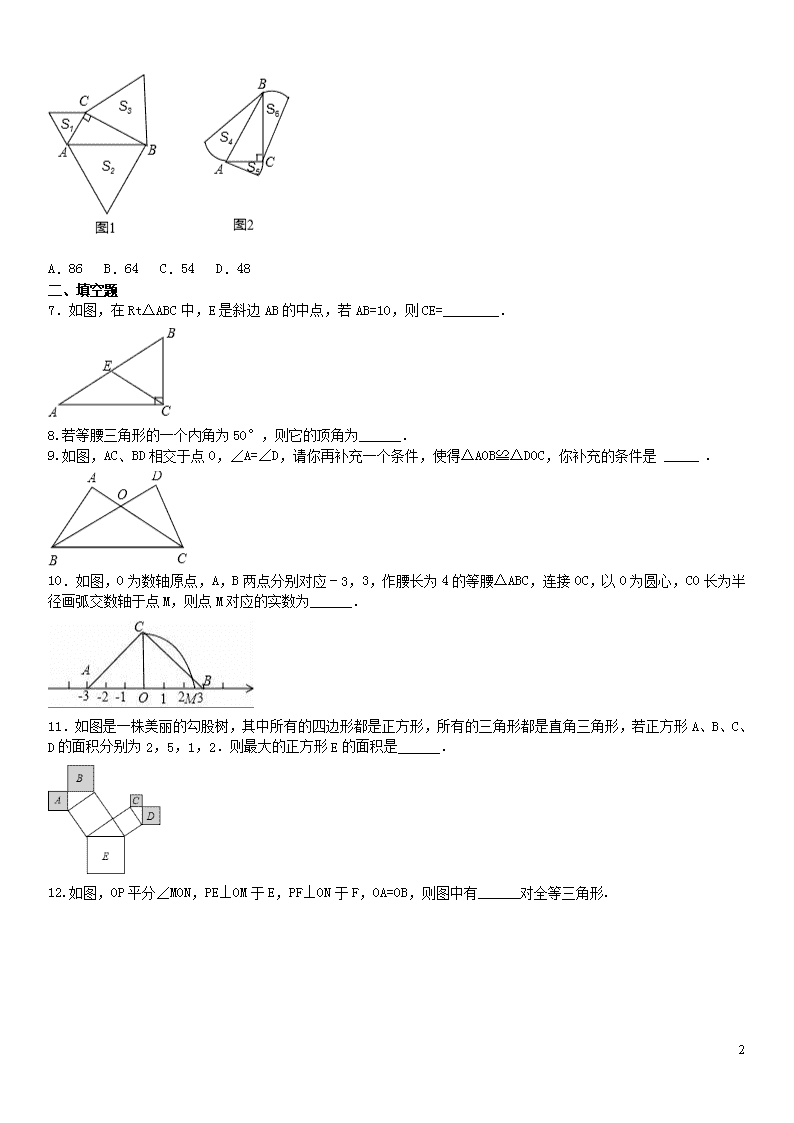‎ ‎5.如图，在△ABC和△DEC中，已知AB=DE，还需添加两个条件才能使△ABC≌△DEC，不能添加的一组条件是（　　）‎ A．BC=EC，∠B=∠E B．BC=EC，AC=DC C．BC=DC，∠A=∠D D．∠B=∠E，∠A=∠D ‎6．如图1，分别以直角三角形三边为边向外作等边三角形，面积分别为S1、S2、S3；如图2，分别以直角三角形三个顶点为圆心，三边长为半径向外作圆心角相等的扇形，面积分别为S4、S5、S6．其中S1=16，S2=45，S5=11，S6=14，则S3+S4=（　　） ‎ 6‎ ‎ ‎ A．86 B．64 C．54 D．48‎ 二、填空题 ‎7．如图，在Rt△ABC中，E是斜边AB的中点，若AB=10，则CE=________．‎ ‎8.若等腰三角形的一个内角为50°，则它的顶角为______．‎ ‎9.如图，AC、BD相交于点O，∠A=∠D，请你再补充一个条件，使得△AOB≌△DOC，你补充的条件是 _____ .‎ ‎10．如图，O为数轴原点，A，B两点分别对应﹣3，3，作腰长为4的等腰△ABC，连接OC，以O为圆心，CO长为半径画弧交数轴于点M，则点M对应的实数为______．‎ ‎11．如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形A、B、C、D的面积分别为2，5，1，2．则最大的正方形E的面积是______．‎ ‎12.如图，OP平分∠MON，PE⊥OM于E，PF⊥ON于F，OA=OB，则图中有______对全等三角形.‎ 6‎ 三、解答题 ‎13.如图，点A、C、D、B四点共线，且AC=BD，∠A=∠B，∠ADE=∠BCF，求证：DE=CF．‎ ‎14．点D，E在△ABC的边BC上，连结AD，AE.①AB＝AC；②AD＝AE；③BD＝CE.以此三个等式中的两个作为命题的题设，另一个作为命题的结论，构成三个命题：①②⇒③；①③⇒②；②③⇒①.‎ ‎(1)以上三个命题是真命题的为(直接作答)______；‎ ‎(2)请选择一个真命题进行证明．(先写出所选命题，然后证明)‎ ‎15．如图，△ABC中，AB=AC，AD⊥BC，CE⊥AB，AE=CE．求证： （1）△AEF≌△CEB； （2）AF=2CD．‎ ‎16. 在△ABC中，AB=15，BC=14，AC=13，求△ABC的面积．‎ 某学习小组经过合作交流，给出了下面的解题思路，请你按照他们的解题思路完成解答过程．‎ ‎ ‎ 参考答案 6‎ ‎1.C 2.Ｃ ‎3．A【解析】在直角三角形AOB中，因为OA=2，OB=7，所以由勾股定理得AB=， 由题意可知AB=A′B′=， 又OA′=3，根据勾股定理得OB′=， ∴BB′=7-＜1．‎ ‎4．B ‎5.C【解析】A选项：已知AB=DE，再加上条件BC=EC，∠B=∠E，可利用SAS证明△ABC≌△DEC，故不合题意； B选项：已知AB=DE，再加上条件BC=EC，AC=DC，可利用SSS证明△ABC≌△DEC，故不合题意； C选项：已知AB=DE，再加上条件BC=DC，∠A=∠D，不能证明△ABC≌△DEC，故符合题意； D选项：已知AB=DE，再加上条件∠B=∠E，∠A=∠D，可利用ASA证明△ABC≌△DEC，故不合题意。‎ 故选C．‎ ‎6．C【解析】S1=AC2，S2=AB2，S3=BC2， ∵BC2=AB2-AC2， ∴S2-S1=S3， S4=S5+S6， ∴S3+S4=45-16+11+14=54． 故选C．‎ ‎7．5‎ ‎8.50°或80°‎ ‎9.AO=DO或AB=DC或BO=CO ‎【解析】添加AO=DO或AB=DC或BO=CO后可分别根据ASA、AAS、AAS判定△AOB≌△DOC． 故填AO=DO或AB=DC或BO=CO．‎ ‎10．‎ ‎11.10【解析】根据勾股定理的几何意义，可得A、B的面积和为S1，C、D的面积和为S2，S1+S2=S3，于是S3=S1+S2，即S3=2+5+1+2=10．‎ 6‎ ‎12.3【解析】由OP平分∠MON，PE⊥OM于E，PF⊥ON于F，得到PE=PF，∠1=∠2，证得△AOP≌△BOP，再根据△AOP≌△BOP，得出AP=BP，于是证得△AOP≌△BOP，‎ 和Rt△AOP≌Rt△BOP．‎ ‎13.证明：∵AC=BD， ∴AC+CD=BD+CD， ∴AD=BC， 在△AED和△BFC中， ‎ ‎∴△AED≌△BFC（ASA）， ∴DE=CF．‎ ‎14．解：(1)①②⇒③；①③⇒②；②③⇒①‎ ‎(2)选择①③⇒②进行证明。‎ 证明：∵AB＝AC，∴∠B＝∠C，‎ 又∵BD＝CE，‎ ‎∴△ABD≌△ACE，‎ ‎∴AD＝AE.‎ ‎15．证明：（1）∵AD⊥BC，CE⊥AB， ∴∠BCE+∠CFD=90°，∠BCE+∠B=90°， ∴∠CFD=∠B， ∵∠CFD=∠AFE， ∴∠AFE=∠B。 在△AEF与△CEB中， ‎ ‎∴△AEF≌△CEB（AAS）.‎ ‎（2）∵AB=AC，AD⊥BC， ∴BC=2CD， ∵△AEF≌△CEB， ∴AF=BC， ∴AF=2CD．‎ ‎16. 解：如图，在△ABC中，AB=15，BC=14，AC=13，‎ 设，∴．‎ 由勾股定理得：， ‎ 6‎ ‎，‎ ‎∴，‎ 解得．‎ ‎∴． ‎ ‎∴．‎ 6‎