鄂尔多斯专版2020中考数学复习方案第二单元方程组与不等式组第05课时一次方程组及其应用课件 32页

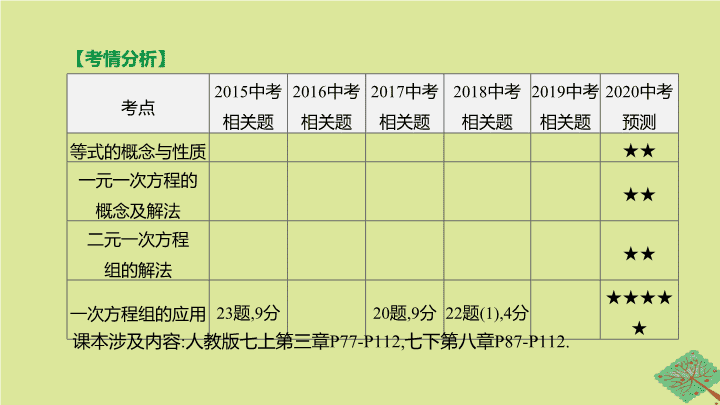
第 5 课时 一次方程 ( 组 ) 及其应用 第二单元　方程 ( 组 ) 与不等式 ( 组 ) 考点 2015 中考 相关题 2016 中考 相关题 2017 中考 相关题 2018 中考 相关题 2019 中考 相关题 2020 中考预测 等式的概念与性质 ★★ 一元一次方程的 概念及解法 ★★ 二元一次方程 组的解法 ★★ 一次方程组的应用 23 题 ,9 分 20 题 ,9 分 22 题 (1),4 分 ★★★★★ 【 考情分析 】 课本涉及内容 : 人教版七上第三章 P77-P112, 七下第八章 P87-P112. 1 . 方程 : 含有未知数的 ① 　　　　 .  2 . 方程的解 : 使方程中等号左右两边相等的未知数的值 . 3 . 一元一次方程的一般形式 : ② 　　　　 .  4 . 二元一次方程的一般形式 : ③ 　　　　 .  考点一　方程的有关概念 考点聚焦 等式 ax + b =0( a , b 为常数 , 且 a ≠0) ax + by + c =0( a , b , c 为常数 , 且 a ≠0, b ≠0) 6 . 二元一次方程组的解 : 二元一次方程组的两个方程的公共解 . 考点二　一次方程 ( 组 ) 的解法 = bc 2 . 解一元一次方程的一般步骤 ( 解方程过程中常会用到等式的性质 ): 3 . 二元一次方程组的解法 : (1) 思想 : 二元一次方程组 一元一次方程 . (2) 方法 : 方法 说明 代入法 　 适用于有一个方程中某个未知数的系数为 1 或 -1 的情况 加减法 　 在方程两边同乘以一个数 , 将两个方程中同一个未知数的系数变为相同的数 ( 或互为相反数 ), 再将方程两边分别相减 ( 或相加 ) 考点三　一次方程 ( 组 ) 的实际应用 图 5-1 【 温馨提示 】 设未知数列方程是关键 , 求解时注意两点 :(1) 设适当的未知数 ;(2) 题中各个量的单位 . 题组一　必会题 对点演练 A B B 2 . 已知 x =3 是关于 x 的方程 2 x - a =1 的解 , 则 a 的值为 ( 　　 ) A . -5 B . 5 C . 7 D . -7 8 题组二　易错题 【 失分点 】 运用等式的性质 , 将等式两边乘同一个数时 , 忘记乘常数项 ; 利用加减法解二元一次方程组时 , 两个方程相减时 , 出现符号错误 . C B 考向一　等式的概念及性质 [ 答案 ] (1)× 　 (2)√ 　 (3)× 　 (4)× [ 解析 ] (1) 利用等式性质 1, 两边都加 c , 得到 a + c = b + c , 所以错误 ; (2) 利用等式性质 2, 两边都乘 c , 得到 a = b , 所以正确 ; (3) 因为 c 不能为 0, 所以错误 ; (4) 因为 a 2 =9,3 a 2 =27, 所以 a 2 ≠3 a 2 , 所以错误 . | 考向精练 | B [ 答案 ] a 　 [ 解析 ] 当两个天平都平衡时 , 2 a =3 b ,2 b =3 c. 由等式的性质 , 得 4 a =6 b ,6 b =9 c , 即 4 a =6 b =9 c , 则质量最大的物体是 a. 2 . 如图 5-2, 天平中的物体 a , b , c 使天平处于平衡状态 , 则质量最大的物体是 　　　　 .  图 5-2 考向二　一元一次方程的解法 解 :(1) 去括号 , 得 7 x -4=3 x +6, 移项、合并同类项 , 得 4 x =10, 系数化为 1, 得 x =2 . 5 . (2) 去分母 , 得 2(2 x +5)-24=3( x -3), 去括号 , 得 4 x +10-24=3 x -9, 移项、合并同类项 , 得 x =5 . 【 方法点析 】 去分母时 , 要注意两点 :(1) 不要漏乘不含分母的项 ;(2) 当分子是多项式时 , 要对分子添括号 . | 考向精练 | B 解 : 去分母 , 得 2 x -3(30- x )=60, 去括号 , 得 2 x -90+3 x =60, 移项 , 得 2 x +3 x =60+90, 合并同类项 , 得 5 x =150, 系数化为 1, 得 x =30 . 考向三　二元一次方程组的解法 | 考向精练 | 1 . [2019· 苏州 ] 若 a +2 b =8,3 a +4 b =18, 则 a + b 的值为 　　　　 .  [ 答案 ] 5 　 [ 解析 ] ∵ a +2 b =8, ∴ a =8-2 b , 代入 3 a +4 b =18 中 , 解得 b =3, 则 a =2, 故 a + b =5 . 故答案为 5 . [ 答案 ] 3 　 [ 解析 ] 方法一 : 解方程组得 m =2, n =1, 所以 m 2 - n 2 =2 2 -1 2 =3 . 方法二 : 方程组两式两边分别相乘得 m 2 - n 2 =3 . 考向四　利用一次方程 ( 组 ) 解决生活实际问题 例 4 某校食堂的午餐与晚餐的资费标准如下表: 小杰同学某星期从周一到周五每天的午餐与晚餐均在学校选用 A 类或 B 类中的一份套餐菜与一份米饭 , 这五天共消费 36 元 . 请问 : 小杰在这五天内 ,A,B 类套餐菜分别选用了多少次 ? 种类 单价 米饭 0 . 5 元 / 份 A 类套餐菜 3 . 5 元 / 份 B 类套餐菜 2 . 5 元 / 份 | 考向精练 | [ 答案 ] B [ 答案 ] 250 　 [ 解析 ] 设速度快的人走的时间为 x , 根据题意可得 , 100 x =100+60 x , 所以 x =2 . 5, 所以速度快的人要走 100×2 . 5=250( 步 ) 才能追到速度慢的人 . 2 . [2019· 株洲 ] 《 九章算术 》 是我国古代内容极为丰富的数学名著 , 书中有如下问题 :“ 今有善行者行一百步 , 不善行者行六十步 . 今不善行者先行一百步 , 善行者追之 , 问几何步及之 ?” 其意思为 : 速度快的人走 100 步 , 速度慢的人只走 60 步 , 现速度慢的人先走 100 步 , 速度快的人去追赶 , 则速度快的人要走 　　　　 步才能追到速度慢的人 .  数学文化 3 . [2019· 烟台 ] 亚洲文明对话大会召开期间 , 大批的大学生志愿者参与服务工作 . 某大学计划组织本校全体志愿者统一乘车去会场 , 若单独调配 36 座新能源客车若干辆 , 则有 2 人没有座位 ; 若只调配 22 座新能源客车 , 则用车数量将增加 4 辆 , 并空出 2 个座位 . (1) 计划调配 36 座新能源客车多少辆 ? 该大学共有多少名志愿者 ? (2) 若同时调配 36 座和 22 座两种车型 , 既保证每人有座 , 又保证每车不空座 , 则两种车型各需多少辆 ? 3 . [2019· 烟台 ] 亚洲文明对话大会召开期间 , 大批的大学生志愿者参与服务工作 . 某大学计划组织本校全体志愿者统一乘车去会场 , 若单独调配 36 座新能源客车若干辆 , 则有 2 人没有座位 ; 若只调配 22 座新能源客车 , 则用车数量将增加 4 辆 , 并空出 2 个座位 . (2) 若同时调配 36 座和 22 座两种车型 , 既保证每人有座 , 又保证每车不空座 , 则两种车型各需多少辆 ?