相似三角形的周长与面积1 6页

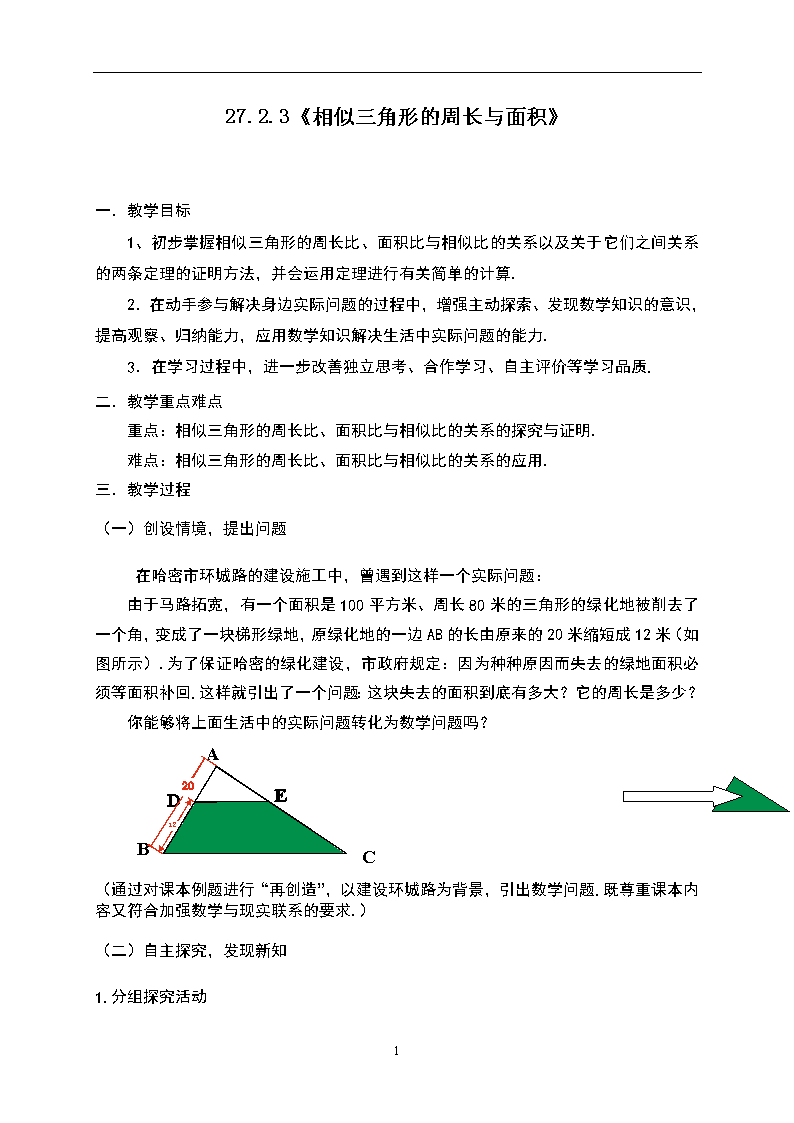
‎ ‎ ‎27.2.3《相似三角形的周长与面积》‎ 一．教学目标 ‎1、初步掌握相似三角形的周长比、面积比与相似比的关系以及关于它们之间关系的两条定理的证明方法，并会运用定理进行有关简单的计算.‎ ‎2．在动手参与解决身边实际问题的过程中，增强主动探索、发现数学知识的意识，提高观察、归纳能力，应用数学知识解决生活中实际问题的能力.‎ ‎3．在学习过程中，进一步改善独立思考、合作学习、自主评价等学习品质.‎ 二．教学重点难点 重点：相似三角形的周长比、面积比与相似比的关系的探究与证明.‎ 难点：相似三角形的周长比、面积比与相似比的关系的应用.‎ 三．教学过程 （一） 创设情境，提出问题 在哈密市环城路的建设施工中，曾遇到这样一个实际问题：‎ 由于马路拓宽，有一个面积是100平方米、周长80米的三角形的绿化地被削去了一个角，变成了一块梯形绿地，原绿化地的一边AB的长由原来的20米缩短成12米（如图所示）.为了保证哈密的绿化建设，市政府规定：因为种种原因而失去的绿地面积必须等面积补回.这样就引出了一个问题：这块失去的面积到底有多大？它的周长是多少？‎ 你能够将上面生活中的实际问题转化为数学问题吗？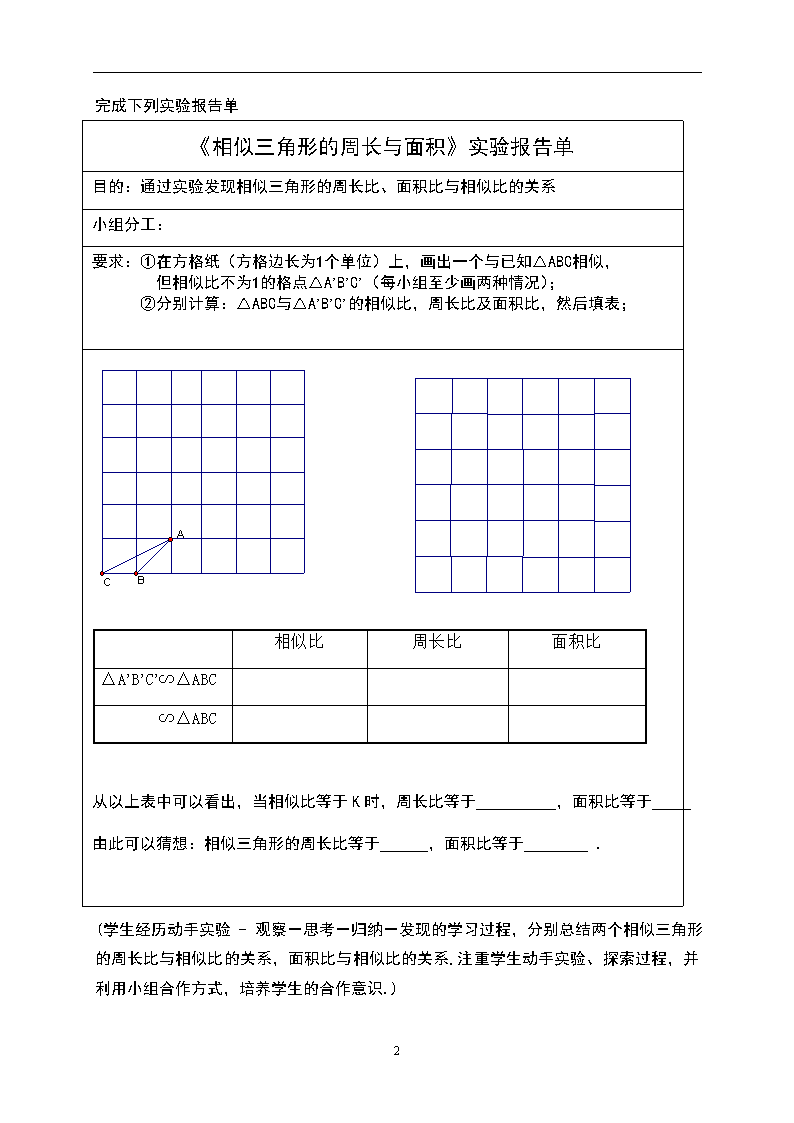‎ ‎ ‎ ‎ ‎ ‎（通过对课本例题进行“再创造”，以建设环城路为背景，引出数学问题.既尊重课本内容又符合加强数学与现实联系的要求.）‎ ‎（二）自主探究，发现新知 ‎1.分组探究活动 6‎ ‎ ‎ 完成下列实验报告单 ‎ ‎ 从以上表中可以看出，当相似比等于K时，周长比等于 ，面积比等于 .‎ ‎ ‎ 由此可以猜想：相似三角形的周长比等于 ，面积比等于 .‎ ‎ 从以上表中可以看出，当相似比等于K时，面积比等于 ，周长比等于 .‎ ‎ 由此可以猜想：相似三角形的面积比等于 ，周长比于 . ‎ 要求：①在方格纸（方格边长为1个单位）上，画出一个与已知△ABC相似，‎ ‎ 但相似比不为1的格点△A’B’C’（每小组至少画两种情况）；‎ ‎ ②分别计算：△ABC与△A’B’C’的相似比，周长比及面积比，然后填表； ‎ 小组分工：‎ 目的：通过实验发现相似三角形的周长比、面积比与相似比的关系 ‎《相似三角形的周长与面积》实验报告单 ‎ ‎ ‎(学生经历动手实验 - 观察－思考－归纳－发现的学习过程，分别总结两个相似三角形的周长比与相似比的关系，面积比与相似比的关系.注重学生动手实验、探索过程，并利用小组合作方式，培养学生的合作意识.)‎ 6‎ ‎ ‎ 附件1:通过上一节课完成的实验报告单,让学生回答实验报告单中的思考作业.‎ 思考作业：猜想相似三角形的周长比、面积比与相似比有怎样的关系？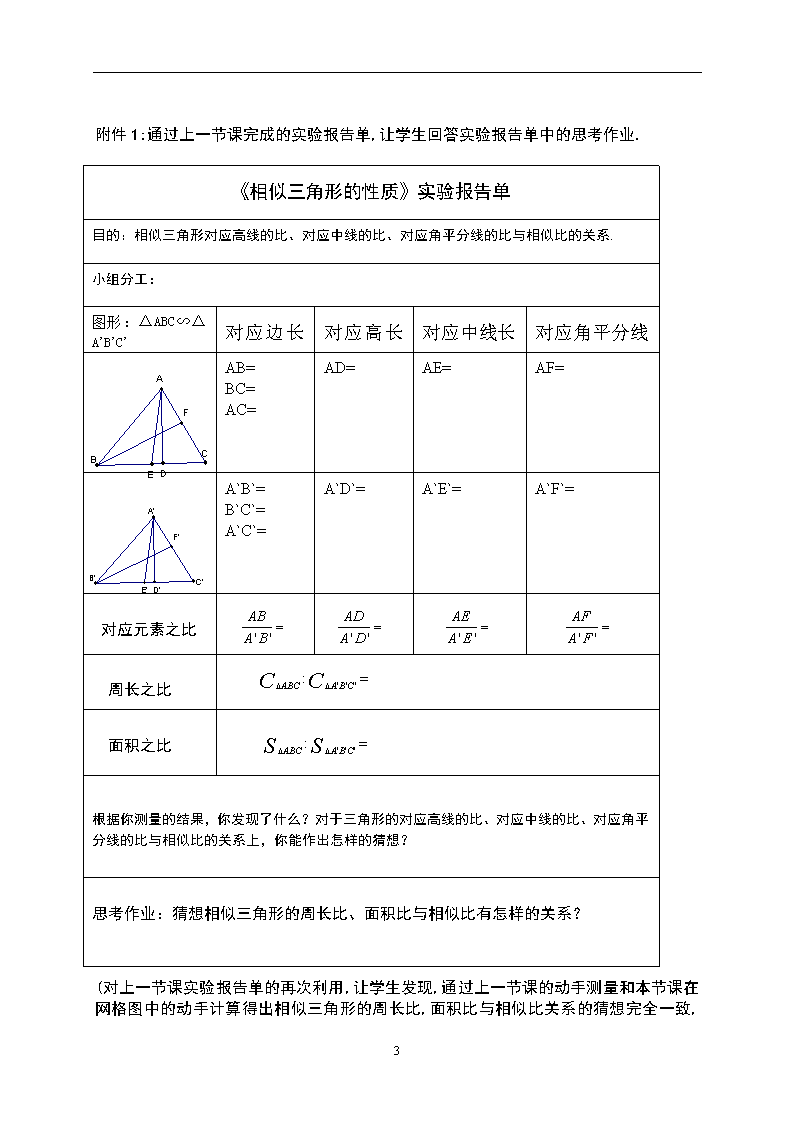‎ 根据你测量的结果，你发现了什么？对于三角形的对应高线的比、对应中线的比、对应角平分线的比与相似比的关系上，你能作出怎样的猜想？‎ AF=‎ 对应角平分线长度（cm）‎ AE=‎ 对应中线长度（cm）‎ AD=‎ 对应高长度（cm）‎ AB=‎ BC=‎ AC=‎ 对应边长度（cm）‎ A`F`=‎ A`E`=‎ A`D`=‎ 小组分工：‎ A`B`=‎ B`C`=‎ A`C`=‎ 面积之比 周长之比 对应元素之比 图形：△ABC∽△A’B’C’‎ 目的：相似三角形对应高线的比、对应中线的比、对应角平分线的比与相似比的关系.‎ ‎《相似三角形的性质》实验报告单 6‎ ‎ ‎ ‎(对上一节课实验报告单的再次利用,让学生发现,通过上一节课的动手测量和本节课在网格图中的动手计算得出相似三角形的周长比,面积比与相似比关系的猜想完全一致,再次证明学生猜想的正确性.)‎ 猜测得到命题：相似三角形的周长比等于相似比.‎ ‎ 相似三角形的面积比等于相似比的平方.‎ ‎2．证明所得命题 已知：如图，△∽△，相似比为k，‎ 求证： ，．‎ 证明：‎ ‎△∽△‎ ‎ ‎ ‎．‎ 分别过A、A’作△ABC, △A’B’C’ 的高AD,A’D’‎ ‎ ‎ ‎△∽△‎ ‎、分别是△、△的高 ‎ ‎ ‎ ‎ ‎ ‎ ‎．‎ ‎（基于对网格具有支架作用的认识，同时考虑到学生学习相似三角形的判定时对网格图已有接触、比较熟悉，所以探究活动选择网格图上的格点三角形进行研究，便于学生进行边长、周长、面积的计算.探究活动①的设计，复旧育新，不但复习了相似三角形的判定，同时为新知识的获取创造条件.）‎ ‎（三）运用性质，熟悉新知 6‎ ‎ ‎ 1． 已知两个三角形相似，根据下列数据填表：‎ 相似比 ‎2‎ ‎1/3‎ 周长比 ‎0.01‎ ‎10‎ 面积比 ‎10000‎ ‎0.0001‎ 2． 实际问题的解决 如图，已知，在△中，‎ DE∥BC,AB=20m,BD=12m, △的周长为80m，面积为100m2,求：△的周长和面积．‎ ‎（通过探索、论证，到运用解决实际问题，一方面学生摸索到了从已知到未知的研究方法，另一方面又感受到了数学来源于生活又服务于生活.）‎ ‎3．引申 分别连结CD和BE交于点G，‎ 求：(1)‎ ‎(2)，‎ ‎(3)，，，.‎ ‎ ‎ ‎（对引例的变式是培养学生多层次、多角度思维能力的一种较好形式.复杂图形中观察基本图形对学生来说有一定的难度，教师借助于多媒体的力量，采用图形的闪烁，色彩的变化等手段，突出基本图形，突破难点.）‎ 6‎ ‎ ‎ ‎（四）小结反思, 自主评价 ‎1. 知识技能部分的小结：‎ 相似三角形的周长比、面积比与相似比的关系；两条有关定理的证明思路与证明方法；定理的运用（进行有关简单的计算）.‎ ‎ 2．自主评价：‎ 如：对网格图上的两个格点三角形相似的认识；对运用定理解决问题的注意点的反思性总结；对自己及同伴在课堂上数学学习表现的评价；提出自己的困惑与不解，或进行质疑等.‎ ‎3. 教师根据学生自主评价情况作适当的点评.‎ ‎（五）分层作业，着眼发展 1. 必做题： P54 习题27.2 第6题.‎ 2. 选做题：(1)对引例继续探究 过点E作EF//AB，EF交BC于点F,其他条件不变，则的面积等于多少？平行四边形DBFE面积为多少？‎ ‎(2)猜想相似多边形的周长比,面积比与相似比有怎样的关系?‎ ‎(作业的布置,帮助学生对知识的保持和迁移,尊重学生的个体差异满足多样化的学习需要,使不同层次的学生有不同的收获.)‎ ‎（六）课后反思：‎ 6‎