鄂尔多斯专版2020中考数学复习方案第四单元三角形第20课时相似三角形及其应用课件 53页

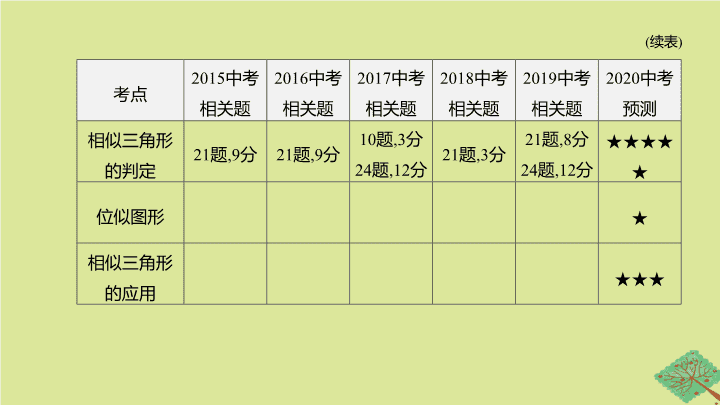
第 20 课时 相似三角形及其应用 第四单元　三角形 【 考情分析 】 考点 2015 中考 相关题 2016 中考 相关题 2017 中考 相关题 2018 中考 相关题 2019 中考 相关题 2020 中考 预测 相似图形 ★ 平行线分 线段成比例 ★ 相似三角形 的 性质 21 题 ,9 分 21 题 ,9 分 21 题 ,8 分 24 题 ,12 分 ★★★★★ 考点 2015 中考 相关题 2016 中考 相关题 2017 中考 相关题 2018 中考 相关题 2019 中考 相关题 2020 中考 预测 相似三角形 的 判定 21 题 ,9 分 21 题 ,9 分 10 题 ,3 分 24 题 ,12 分 21 题 ,3 分 21 题 ,8 分 24 题 ,12 分 ★★★★★ 位似图形 ★ 相似三角形 的 应用 ★★★ ( 续表 ) 考点一　比例线段的相关概念及性质 考点聚焦 1 . 线段的比 : 两条线段的比是两条线段的长度之比 . ad 　 3 . 比例的基本性质 ac 两 　 考点二　平行线分线段成比例 图 20-1 图 20-2 考点三　相似三角形的性质及判定 1. 相似三角形的性质及判定 判定 (1) 平行于三角形一边的直线和其他两边相交 , 所构成的三角形与原三角形相似 ; (2) 三边成比例的两个三角形 ⑦ 　　　 ;  (3) 两边成比例且 ⑧ 　　　 相等的两个三角形相似 ;  (4) 两角分别相等的两个三角形相似 ; (5) 两直角三角形的斜边和一条直角边对应成比例 , 两直角三角形相似 性质 (1) 相似三角形的对应角相等 , 对应边成比例 ; (2) 相似三角形对应高的比、对应中线的比与对应角平分线的比都等于相似比 ; (3) 相似三角形周长的比等于 ⑨ 　　　 , 相似三角形面积的比等于 ⑩ 　　 　 . 相似 夹角 相似比 相似比的平方 考点四　相似多边形 1 . 定义 : 两个边数相同的多边形 , 如果它们的角分别相等 , 边成比例 , 那么这两个多边形叫做相似多边形 , 相似多边形对应边的比叫做相似比 . 2 . 性质 (1) 相似多边形的对应角 ⑪ 　　　　 ;  (2) 相似多边形的对应边 ⑫ 　　　　 ;  (3) 相似多边形的周长比 ⑬ 　　　　 相似比 , 面积比等于 ⑭ 　 　　　 .  相等 成比例 等于 相似比的平方 考点五　图形的位似 1 . 定义 : 两个多边形不仅相似 , 而且对应顶点的连线相交于一点 , 对应边互相平行 ( 或在同一直线上 ), 像这样的两个图形叫做位似图形 , 这点叫做位似中心 . 2 . 基本图形 : 图 20-3 3 . 性质 (1) 位似图形上的任意一对对应点到位似中心的距离的比等于 ⑮ 　　　　 ;  (2) 位似图形对应点的连线或延长线相交于 ⑯ 　　　　 点 ;  (3) 位似图形对应边 ⑰ 　　　　 ( 或在同一条直线上 );  (4) 位似图形对应角相等 . 4 . 作图步骤 (1) 确定位似中心 ; (2) 确定原图形中各顶点关于位似中心的对应点 ; (3) 描出新图形 . 相似比 一 平行 考点六　相似三角形的应用 几何图形的 证明 与计算 常见问题 　 证明线段的数量关系 , 求线段的长度 , 图形的面积等 相似三角形 在 实际生活 中 的应用 建模思想 建立相似三角形模型 常见题 目类型 (1) 利用投影、平行线、标杆等构造相似三角形求解 ; (2) 计算从底部能直接测量的物体的高度 ; (3) 计算从底部不能直接测量的物体的高度 ; (4) 计算不能直接测量的河的宽度 题组一　必会题 对点演练 C 图 20-4 2 . [2018· 铜仁 ] 已知 △ ABC ∽△ DEF , 相似比为 2, 且 △ ABC 的面积为 16, 则 △ DEF 的面积为 ( 　　 ) A . 32 B . 8 C . 4 D . 16 C 3 . 如图 20-5, 小正方形的边长均为 1, 则下列图中的三角形 ( 阴影部分 ) 与 △ ABC 相似的是 ( 　　 ) 图 20-5 图 20-6 [ 答案 ] B 图 20-7 [ 答案 ] B [ 答案 ] (-1,2) 或 (1,-2) 【 失分点 】 写比例式时对应关系找错 ; 在比例式的转化中出错 ; 忽视相似三角形中可能存在的不同的对应关系 . 题组二　易错题 图 20-8 [ 答案 ] C 7 . 如图 20-9, 在 △ ABC 中 , DE ∥ BC , 过点 A 作 AM ⊥ BC 于点 M , 交 DE 于点 N , 若 S △ ADE ∶ S △ ABC =4 ∶ 9, 则 AN ∶ NM 的值是 ( 　　 ) A . 4 ∶ 9 B . 3 ∶ 2 C . 9 ∶ 4 D . 2 ∶ 1 图 20-9 [ 答案 ] D 8 . 如果一个直角三角形的两条边长分别是 6 和 8, 另一个与它相似的直角三角形的边长分别是 3,4 及 x , 那么 x 的值 ( 　　 ) A . 只有 1 个 B . 可以有 2 个 C . 可以有 3 个 D . 有无数个 [ 答案 ] B 9 . 如图 20-10, P 为 Rt△ ABC 斜边 AB 上任意一点 ( 除 A , B 外 ), 过点 P 作直线截 △ ABC , 使截得的新三角形与 △ ABC 相似 , 满足这样条件的直线的作法共有 ( 　　 ) A . 1 种 　　　 　　 B . 2 种 C . 3 种 　　　 　　 D . 4 种 图 20-10 [ 答案 ] C 　 [ 解析 ] 如图 , 过点 P 可作 PE ∥ BC 或 PE″ ∥ AC , 可得相似三角形 , 过点 P 还可作 PE' ⊥ AB , 则∠ E'PA = ∠ C =90°, ∠ A = ∠ A , ∴ △ APE' ∽△ ACB , ∴共有 3 条 . 故选 C . 考向一　比例线段 图 20-11 (1)(4) 图 20-12 [ 答案 ] 2 | 考向精练 | 考向二　相似三角形的性质与判定 例 2 [2019· 凉山州 ] 如图 20-13, ∠ ABD = ∠ BCD =90°, DB 平分∠ ADC , 过点 B 作 BM ∥ CD 交 AD 于 M. 连接 CM 交 DB 于 N. (1) 求证 : BD 2 = AD · CD ; (2) 若 CD =6, AD =8, 求 MN 的长 . 图 20-13 分析 :(1) 利用两角分别相等证 △ DAB ∽△ DBC , 再由相似性质得到结论 ; 例 2 [2019· 凉山州 ] 如图 20-13, ∠ ABD = ∠ BCD =90°, DB 平分∠ ADC , 过点 B 作 BM ∥ CD 交 AD 于 M. 连接 CM 交 DB 于 N. (2) 若 CD =6, AD =8, 求 MN 的长 . 图 20-13 分析 : (2) 先利用相似性质与勾股定理求 BD , AB 的长 , 再借助角的关系得到 △ ABM 是等边三角形 , 求得 BM 的长 , 最后利用相似和勾股定理求 BC , CM , MN 的长 . | 考向精练 | 图 20-14 [ 答案 ] C 2 . [2018· 包头 ] 如图 20-15, 在▱ ABCD 中 , AC 是一条对角线 , EF ∥ BC , 且 EF 与 AB 相交于点 E , 与 AC 相交于点 F ,3 AE =2 EB , 连接 DF. 若 S △ AEF =1, 则 S △ ADF 的值为 　　　　 .  图 20-15 3 . [2019· 长春 ] 教材呈现 : 下图是华师版九年级上册数学教材第 78 页的部分内容 . 图 20-16 3 . [2019· 长春 ] 教材呈现 : 下图是华师版九年级上册数学教材第 78 页的部分内容 . 图 20-16 3 . [2019· 长春 ] 教材呈现 : 下图是华师版九年级上册数学教材第 78 页的部分内容 . 图 20-16 [ 答案 ] (2)6 . 考向三　位似 例 3 [2017· 烟台 ] 如图 20-17, 在直角坐标系中 , 每个小方格的边长均为 1 . △ AOB 与 △ A'OB' 是以原点 O 为位似中心的位似图形 , 且相似比为 3 ∶ 2, 点 A , B 都在格点上 , 则点 B' 的坐标是 　　　　 .  图 20-17 | 考向精练 | [2018· 菏泽 ] 如图 20-18,△ OAB 与 △ OCD 是以点 O 为位似中心的位似图形 , 相似比为 3 ∶ 4, ∠ OCD =90°, ∠ AOB =60°, 若点 B 的坐标是 (6,0), 则点 C 的坐标是 　 　　 .  图 20-18