2017-2018学年山东省临沂市莒南县九年级上期中数学试卷含答案解析 23页

‎2017-2018学年山东省临沂市莒南县九年级（上）期中数学试卷 ‎　‎ 一、选择题（本大题共14小题，每小题3分，共42分）‎ ‎1．（3分）用配方法解一元二次方程x2﹣6x﹣10=0时，下列变形正确的为（　　）‎ A．（x+3）2=1 B．（x﹣3）2=1 C．（x+3）2=19 D．（x﹣3）2=19‎ ‎2．（3分）关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根，则k的取值范围是（　　）‎ A．k＞﹣1 B．k＜1 C．k＞﹣1且k≠0 D．k＜1且k≠0‎ ‎3．（3分）如图，A、B、C是⊙O上的三点，∠BOC=70°，则∠A的度数为（　　）‎ A．70° B．45° C．40° D．35°‎ ‎4．（3分）从下列直角三角板与圆弧的位置关系中，可判断圆弧为半圆的是（　　）‎ A． B． C． D．‎ ‎5．（3分）PA，PB分别切⊙O于A，B两点，点C为⊙O上不同于AB的任意一点，已知∠P=40°，则∠ACB的度数是（　　）‎ A．70° B．110° C．70°或110° D．不确定 ‎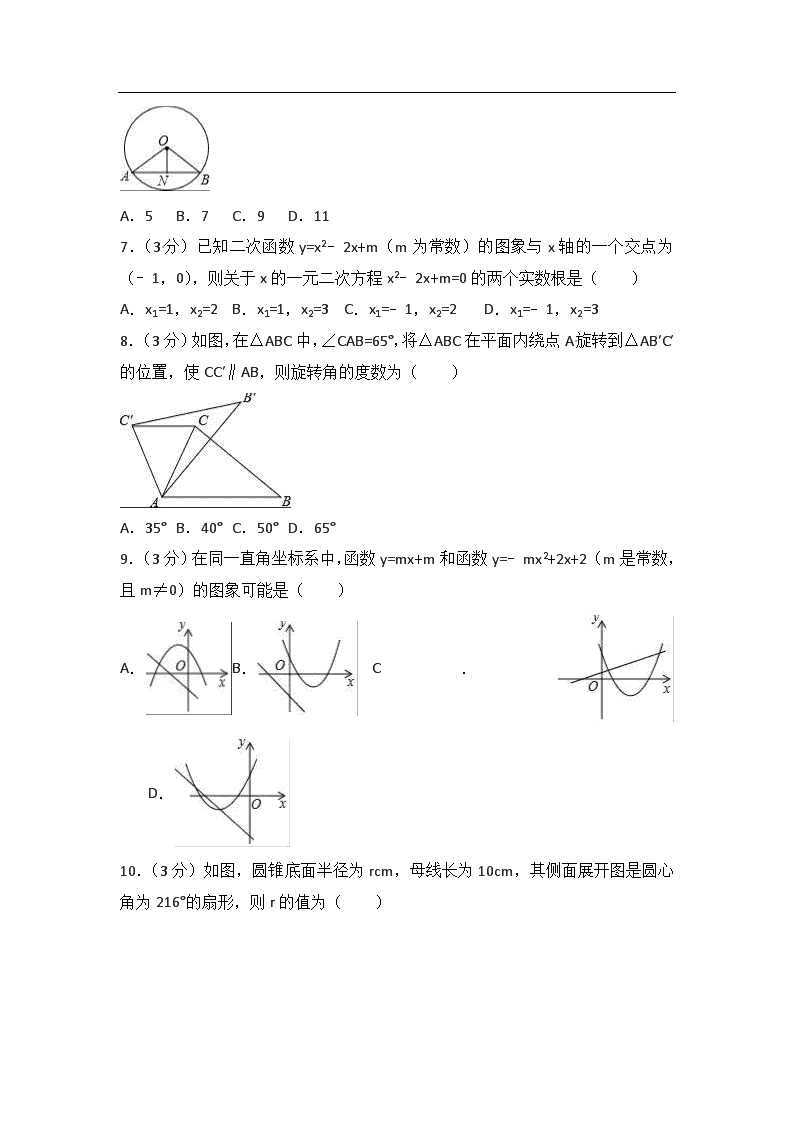6．（3分）如图所示，⊙O的半径为13，弦AB的长度是24，ON⊥AB，垂足为N，则ON=（　　）‎ A．5 B．7 C．9 D．11‎ ‎7．（3分）已知二次函数y=x2﹣2x+m（m为常数）的图象与x轴的一个交点为（﹣1，0），则关于x的一元二次方程x2﹣2x+m=0的两个实数根是（　　）‎ A．x1=1，x2=2 B．x1=1，x2=3 C．x1=﹣1，x2=2 D．x1=﹣1，x2=3‎ ‎8．（3分）如图，在△ABC中，∠CAB=65°，将△ABC在平面内绕点A旋转到△AB′C′的位置，使CC′∥AB，则旋转角的度数为（　　）‎ A．35° B．40° C．50° D．65°‎ ‎9．（3分）在同一直角坐标系中，函数y=mx+m和函数y=﹣mx2+2x+2（m是常数，且m≠0）的图象可能是（　　）‎ A． B． C． D．‎ ‎10．（3分）如图，圆锥底面半径为rcm，母线长为10cm，其侧面展开图是圆心角为216°的扇形，则r的值为（　　）[来源:学,科,网]‎ A．3 B．6 C．3π D．6π ‎11．（3分）在一个不透明的袋子里装有四个小球，球上分别标有6，7，8，9四个数字，这些小球除数字外都相同．甲、乙两人玩“猜数字”游戏，甲先从袋中任意摸出一个小球，将小球上的数字记为m，再由乙猜这个小球上的数字，记为n．如果m，n满足|m﹣n|≤1，那么就称甲、乙两人 “心领神会”，则两人“心领神会”的概率是（　　）‎ A． B． C． D．‎ ‎12．（3分）某广场有一喷水池，水从地面喷出，如图，以水平地面为x轴，出水点为原点，建立平面直角坐标系，水在空中划出的曲线是抛物线y=﹣x2+4x（单位：米）的一部分，则水喷出的最大高度是（　　）‎ A．4米 B．3米 C．2米 D．1米 ‎13．（3分）已知α、β是方程x2﹣3x﹣4=0的两个实数根，则α2+αβ﹣3α的值为（　　）‎ A．0 B．1 C．2 D．3‎ ‎14．（3分）已知二次函数y=ax2+bx+c的图象如图所示，有下列结论：①abc＜0；②a+c＞b；③3a+c＜0；④a+b＞m（am+b）（其中m≠1），其中正确的结论有（　　）‎ A．1个 B．2个 C．3个 D．4个 ‎　‎ 二、填空题（本大题共5小题，每小题3分，共15分）‎ ‎15．（3分）方程x2=x的解是　 　．‎ ‎16．（3分）用“描点法”画二次函数y=ax2+bx+c的图象时，列了如下表格：‎ x ‎…‎ ‎﹣2‎ ‎﹣1‎ ‎0‎ ‎1‎ ‎2‎ ‎…‎ y ‎…‎ ‎6.5‎ ‎﹣4‎ ‎﹣2.5‎ ‎﹣2‎ ‎﹣2.5‎ ‎…‎ 根据表格中的信息回答问题，该二次函数y=ax2+bx+c在x=3时，函数值y=　 　．‎ ‎17．（3分）如图，AB是⊙O的弦，AB=5，点C是⊙O上的一个动点，且∠ACB=45°，若点M、N分别是AB、AC的中点，则MN长的最大值是　 　．‎ ‎18．（3分）若三角形的某一边长等于其外接圆半径，则将此三角形称为等径三角形，该边所对的角称为等径角．已知△ABC是等径三角形，则等径角的度数为　 　．‎ ‎19．（3分）二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，图象过点（﹣1，0），对称轴为直线x=2，下列结论：（1）4a+b=0；（2）4a+c＞2b；（3）5a+3c＞0；（4）若点A（﹣2，y1），点B（，y2），点C（，y3）在该函数图象上，则y1＜y3＜y2；（5）若m≠2，则m（am+b）＜2（2a+b），其中正确的结论的序号是　 　．‎ ‎　‎ 三、解答题（本大题共7小题，共63分）‎ ‎20．（7分）已知关于x的方程x2﹣2（k﹣2）x+k2=0有两个实数根x1，x2．‎ ‎（1）求k的取值范围；‎ ‎（2）若x1+x2=1﹣x1x2，求k的值．‎ ‎21．（7分）不透明的口袋里装有白、黄、蓝三种颜色的乒乓球（除颜色外其余都相同），其中白球有2个，黄球有1个，现从中任意摸出一个是白球的概率为．‎ ‎（1）试求袋中篮球的个数；‎ ‎（2）第一次任意摸一个球（不放回），第二次再摸一个球，请用画树状图或列表格法，求两次摸到都是白球的概率．‎ ‎22．（7分）如图，将△ABC绕点C按顺时针方向旋转至△A′B′C，使点A′落在BC的延长线上．已知∠A=27°，∠B=40°，求则∠ACB′的度数．‎ ‎23．（8分）如图，点A是直线AM与⊙O的交点，点B在⊙O上，BD⊥AM垂足为D，BD与⊙O交于点C，OC平分∠AOB，∠B=60°．‎ ‎（1）求证：AM是⊙O的切线；‎ ‎（2）若DC=2，求图中阴影部分的面积（结果保留π和根号）．‎ ‎24．（10分）某商场试销一种成本为每件50元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于40%，经试销发现，销售量y（件）与销售单价x（元）符合一次函数y=kx+b，且x=60时，y=50；x=70时，y=40．‎ ‎（1）求一次函数y=kx+b的表达式；‎ ‎（2）若该商场获得利润为W元，试写出利润W与销售单价x之间的关系式；销售单价定为多少元时，商场可获得最大利润，最大利润是多少元？‎ ‎25．（10分）阅读资料：我们把顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角，如图1中∠ABC所示．同学们研究发现：P为圆上任意一点，当弦AC经过圆心O时，且AB切⊙O于点A，此时弦切角∠CAB=∠P（图2）．‎ 证明：∵AB切⊙O于点A，∴∠CAB=90°，又∵AC是直径，∴∠P=90°，∴∠CAB=∠P 问题拓展：若AC不经过圆心O（如图3），该结论：弦切角∠CAB=∠P还成立吗？请说明理由．‎ 知识运用：如图4，AD是△ABC中∠BAC的平分线，经过点A的⊙O与BC切于点D，与AB、AC分别相交于E、F．求证：EF∥BC．‎ ‎26．（14分）如图，二次函数y=ax2+bx+c（a≠0）的图象交x轴于A、B两点，交y轴于点D，点B的坐标为（3，0），顶点C的坐标为（1，4）．‎ ‎（1）求二次函数的解析式和直线BD的解析式；‎ ‎（2）点P是直线BD上的一个动点，过点P作x轴的垂线，交抛物线于点M，当点P在第一象限时，求线段PM长度的最大值；‎ ‎（3）在抛物线上是否存在异于B、D的点Q，使△BDQ中BD边上的高为2？若存在求出点Q的坐标；若不存在请说明理由．‎ ‎　‎ ‎2017-2018学年山东省临沂市莒南县九年级（上）期中数学试卷 参考答案与试题解析 ‎　‎ 一、选择题（本大题共14小题，每小题3分，共42分）[来源:Z。xx。k.Com]‎ ‎1．（3分）用配方法解一元二次方程x2﹣6x﹣10=0时，下列变形正确的为（　　）‎ A．（x+3）2=1 B．（x﹣3）2=1 C．（x+3）2=19 D．（x﹣3）2=19‎ ‎【解答】解：方程移项得：x2﹣6x=10，‎ 配方得：x2﹣6x+9=19，即（x﹣3）2=19，‎ 故选D．‎ ‎　‎ ‎2．（3分）关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根，则k的取值范围是（　　）‎ A．k＞﹣1 B．k＜1 C．k＞﹣1且k≠0 D．k＜1且k≠0‎ ‎【解答】解：∵关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根，‎ ‎∴k≠0且△＞0，即（﹣2）2﹣4×k×（﹣1）＞0，‎ 解得k＞﹣1且k≠0．‎ 故选C．‎ ‎　‎ ‎3．（3分）如图，A、B、C是⊙O上的三点，∠BOC=70°，则∠A的度数为（　　）‎ A．70° B．45° C．40° D．35°‎ ‎【解答】解：∵A、B、C是⊙O上的三点，∠BOC=70°，‎ ‎∴∠A=∠BOC=35°．‎ 故选D．‎ ‎　‎ ‎4．（3分）从下列直角三角板与圆弧的位置关系中，可判断圆弧为半圆的是（　　）‎ A． B． C． D．‎ ‎【解答】解：∵直径所对的圆周角等于直角，‎ ‎∴从下列直角三角板与圆弧的位置关系中，可判断圆弧为半圆的是B．‎ 故选：B．‎ ‎　‎ ‎5．（3分）PA，PB分别切⊙O于A，B两点，点C为⊙O上不同于AB的任意一点，已知∠P=40°，则∠ACB的度数是（　　）‎ A．70° B．110° C．70°或110° D．不确定 ‎【解答】解：如图，连接OA、OB，‎ ‎∵PA，PB分别切⊙O于A，B两点，‎ ‎∴∠PAO=∠PBO=90°，‎ ‎∴∠AOB=360°﹣90°﹣90°﹣40°=140°，‎ 当点C1在上时，则∠AC1B=∠AOB=70°，‎ 当点C2在上时，则∠AC2B+∠AC1B=180°，‎ ‎∴∠AC2B=110°，‎ 故选C．‎ ‎　‎ ‎6．（3分）如图所示，⊙O的半径为13，弦AB的长度是24，ON⊥AB，垂足为N，则ON=（　　）‎ A．5 B．7 C．9 D．11‎ ‎【解答】解：由题意可得，‎ OA=13，∠ONA=90°，AB=24，‎ ‎∴AN=12，‎ ‎∴ON=，‎ 故选A．‎ ‎　‎ ‎7．（3分）已知二次函数y=x2﹣2x+m（m为常数）的图象与x轴的一个交点为（﹣1，0），则关于x的一元二次方程x2﹣2x+m=0的两个实数根是（　　）‎ A．x1=1，x2=2 B．x1=1，x2=3 C．x1=﹣1，x2=2 D．x1=﹣1，x2=3[来源:学科网]‎ ‎【解答】解：二次函数y=x2﹣2x+m（m为常数）的对称轴是x=1，[来源:Z*xx*k.Com]‎ ‎（﹣1，0）关于x=1的对称点是（3，0）．‎ 则一元二次方程x2﹣2x+m=0的两个实数根是x1=﹣1，x2=3．‎ 故选D．‎ ‎　‎ ‎8．（3分）如图，在△ABC中，∠CAB=65°，将△ABC在平面内绕点A旋转到△AB′C′的位置，使CC′∥AB，则旋转角的度数为（　　）‎ A．35° B．40° C．50° D．65°‎ ‎【解答】解：∵CC′∥AB，‎ ‎∴∠ACC′=∠CAB=65°，‎ ‎∵△ABC绕点A旋转得到△AB′C′，[来源:Zxxk.Com]‎ ‎∴AC=AC′，‎ ‎∴∠CAC′=180°﹣2∠ACC′=180°﹣2×65°=50°，‎ ‎∴∠CAC′=∠BAB′=50°．[来源:学|科|网]‎ 故选C．‎ ‎　[来源:Z。xx。k.Com]‎ ‎9．（3分）在同一直角坐标系中，函数y=mx+m和函数y=﹣mx2+2x+2（m是常数，且m≠0）的图象可能是（　　）‎ A． B． C． D．‎ ‎【解答】解：A、由函数y=mx+m的图象可知m＜0，即函数y=﹣mx2+2x+2开口方向朝上，与图象不符，故A选项错误；‎ B、由函数y=mx+m的图象可知m＜0，对称轴为x=﹣=﹣=＜0，则对称轴应在y轴左侧，与图象不符，故B选项错误；‎ C、由函数y=mx+m的图象可知m＞0，即函数y=﹣mx2+2x+2开口方向朝下，与图象不符，故C选项错误；‎ D、由函数y=mx+m的图象可知m＜0，即函数y=﹣mx2+2x+2开口方向朝上，对称轴为x=﹣=﹣=＜0，则对称轴应在y轴左侧，与图象相符，故D选项正确；‎ 故选：D．‎ ‎　‎ ‎10．（3分）如图，圆锥底面半径为rcm，母线长为10cm，其侧面展开图是圆心角为216°的扇形，则r的值为（　　）‎ A．3 B．6 C．3π D．6π ‎【解答】解：∵圆锥底面半径为rcm，母线长为10cm，其侧面展开图是圆心角为216°的扇形，‎ ‎∴2πr=×2π×10，解得r=6．‎ 故选B．‎ ‎　‎ ‎11．（3分）在一个不透明的袋子里装有四个小球，球上分别标有6，7，8，9四个数字，这些小球除数字外都相同．甲、乙两人玩“猜数字”游戏，甲先从袋中任意摸出一个小球，将小球上的数字记为m，再由乙猜这个小球上的数字，记为n．如果m，n满足|m﹣n|≤1，那么就称甲、乙两人“心领神会”，则两人“心领神会”的概率是（　　）‎ A． B． C． D．‎ ‎【解答】解：画树状图如下：‎ 由树状图可知，共有16种等可能结果，其中满足|m﹣n|≤1的有10种结果，‎ ‎∴两人“心领神会”的概率是=，‎ 故选：B．‎ ‎　‎ ‎12．（3分）某广场有一喷水池，水从地面喷出，如图，以水平地面为x轴，出水点为原点，建立平面直角坐标系，水在空中划出的曲线是抛物线y=﹣x2+‎ ‎4x（单位：米）的一部分，则水喷出的最大高度是（　　）‎ A．4米 B．3米 C．2米 D．1米 ‎【解答】解：∵水在空中划出的曲线是抛物线y=﹣x2+4x，‎ ‎∴喷水的最大高度就是水在空中划出的抛物线y=﹣x2+4x的顶点坐标的纵坐标，‎ ‎∴y=﹣x2+4x=﹣（x﹣2）2+4，‎ ‎∴顶点坐标为：（2，4），‎ ‎∴喷水的最大高度为4米，‎ 故选A．‎ ‎　‎ ‎13．（3分）已知α、β是方程x2﹣3x﹣4=0的两个实数根，则α2+αβ﹣3α的值为（　　）‎ A．0 B．1 C．2 D．3‎ ‎【解答】解：根据题意得α+β=3，αβ=﹣4，‎ 所以原式=a（α+β）﹣3α ‎=3α﹣3α ‎=0．‎ 故选A．‎ ‎　‎ ‎14．（3分）已知二次函数y=ax2+bx+c的图象如图所示，有下列结论：①abc＜0；②a+c＞b；③3a+c＜0；④a+b＞m（am+b）（其中m≠1），其中正确的结论有（　　）‎ A．1个 B．2个 C．3个 D．4个 ‎【解答】解：①由图象可知：a＜0，c＞0，‎ ‎∵﹣＞0，‎ ‎∴b＞0，‎ ‎∴abc＜0，故此选项正确；‎ ‎②当x=﹣1时，y=a﹣b+c=0，故a+c=b，错误；‎ ‎③当x=3时函数值小于0，y=9a+3b+c=0，且x=﹣=1，‎ 即b=﹣2a，代入得9a﹣6a+c=0，得3a+c=0，故此选项错误；‎ ‎④当x=1时，y的值最大．此时，y=a+b+c，‎ 而当x=m时，y=am2+bm+c，‎ 所以a+b+c＞am2+bm+c，‎ 故a+b＞am2+bm，即a+b＞m（am+b），故此选项正确．‎ 故①④正确．‎ 故选B．‎ ‎　‎ 二、填空题（本大题共5小题，每小题3分，共15分）‎ ‎15．（3分）方程x2=x的解是　x1=0，x2=1　．‎ ‎【解答】解：x2=x，‎ 移项得：x2﹣x=0，‎ 分解因式得：x（x﹣1）=0，‎ 可得x=0或x﹣1=0，‎ 解得：x1=0，x2=1．‎ 故答案为：x1=0，x2=1‎ ‎　‎ ‎16．（3分）用“描点法”画二次函数y=ax2+bx+c的图象时，列了如下表格：‎ x ‎…‎ ‎﹣2‎ ‎﹣1‎ ‎0‎ ‎1‎ ‎2‎ ‎…‎ y ‎…‎ ‎6.5‎ ‎﹣4‎ ‎﹣2.5‎ ‎﹣2‎ ‎﹣2.5‎ ‎…‎ 根据表格中的信息回答问题，该二次函数y=ax2+bx+c在x=3时，函数值y=　﹣4．　．‎ ‎【解答】解：由表格可知当x=0和x=2时，y=﹣2.5，‎ ‎∴抛物线的对称轴为x=1，‎ ‎∴x=3和x=﹣1时的函数值相等，为﹣4，[来源:学.科.网]‎ 故答案为：﹣4．‎ ‎　‎ ‎17．（3分）如图，AB是⊙O的弦，AB=5，点C是⊙O上的一个动点，且∠ACB=45°，若点M、N分别是AB、AC的中点，则MN长的最大值是　　．‎ ‎【解答】解：如图，∵点M，N分别是AB，AC的中点，‎ ‎∴MN=BC，‎ ‎∴当BC取得最大值时，MN就取得最大值，当BC是直径时，BC最大，‎ 连接BO并延长交⊙O于点C′，连接AC′，‎ ‎∵BC′是⊙O的直径，‎ ‎∴∠BAC′=90°．‎ ‎∵∠ACB=45°，AB=5，‎ ‎∴∠AC′B=45°，‎ ‎∴BC′===5，‎ ‎∴MN最大=．‎ 故答案为：．‎ ‎　‎ ‎18．（3分）若三角形的某一边长等于其外接圆半径，则将此三角形称为等径三角形，该边所对的角称为等径角．已知△ABC是等径三角形，则等径角的度数为 ‎　30°或150°　．‎ ‎【解答】解：如图边AB与半径相等时，‎ 则∠AOB=60°，‎ 当等径角顶点为C时，∠C=∠AOB=30°，‎ 当等径角顶点为D时，∠C+∠D=180°，∠D=150°，‎ 故答案为：30°或150°．‎ ‎　‎ ‎19．（3分）二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，图象过点（﹣1，0），对称轴为直线x=2，下列结论：（1）4a+b=0；（2）4a+c＞2b；（3）5a+3c＞0；（4）若点A（﹣2，y1），点B（，y2），点C（，y3）在该函数图象上，则y1＜y3＜y2；（5）若m≠2，则m（am+b）＜2（2a+b），其中正确的结论的序号是　（1）（3）（5）　．‎ ‎【解答】解：∵称轴为直线x=2，‎ ‎∴，‎ ‎∴b=﹣4a，‎ ‎∴4a+b=0，故（1）正确，‎ ‎∵二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，图象过点（﹣1，0），对称轴为直线x=2，‎ ‎∴当x=﹣2时，y=4a﹣2b+c＜0，‎ ‎∴4a+c＜2b，故（2）错误，‎ ‎∵图象过点（﹣1，0），b=﹣4a，c＞0，‎ ‎∴a﹣b+c=0，‎ ‎∴5a+c=0，‎ ‎∴5a+c+2c＞0，‎ ‎∴5a+3c＞0，故（3）正确，‎ ‎∵点A（﹣2，y1），点B（，y2），点C（，y3）在该函数图象上，对称轴为直线x=2，图象开口向下，‎ ‎∴y1＜y2＜y3，故（4）错误，‎ ‎∵当x=2时，y取得最大值，‎ ‎∴当x=m≠2时，am2+bm+c＜4a+2b+c，‎ ‎∴m（am+b）＜2（2a+b），故（5）正确，‎ 故答案为：（1）（3）（5）．‎ ‎　‎ 三、解答题（本大题共7小题，共63分）‎ ‎20．（7分）已知关于x的方程x2﹣2（k﹣2）x+k2=0有两个实数根x1，x2．‎ ‎（1）求k的取值范围；‎ ‎（2）若x1+x2=1﹣x1x2，求k的值．‎ ‎【解答】解：（1）由题意△≥0，‎ ‎∴4（k﹣2）2﹣4k2≥0，‎ ‎∴k≤1．‎ ‎（2）∵x1+x2=2（k﹣2），x1x2=k2，‎ ‎∴2（k﹣2）=1﹣k2，‎ 解得k=﹣1+或﹣1﹣，‎ ‎∵k≤1，‎ ‎∴k=﹣1﹣．[来源:学,科,网Z,X,X,K]‎ ‎　‎ ‎21．（7分）不透明的口袋里装有白、黄、蓝三种颜色的乒乓球（除颜色外其余都相同），其中白球有2个，黄球有1个，现从中任意摸出一个是白球的概率为．‎ ‎（1）试求袋中篮球的个数；‎ ‎（2）第一次任意摸一个球（不放回），第二次再摸一个球，请用画树状图或列表格法，求两次摸到都是白球的概率．‎ ‎【解答】解：（1）设袋中蓝球的个数为x个，‎ ‎∵从中任意摸出一个是白球的概率为，‎ ‎∴=，‎ 解得：x=1，‎ ‎∴袋中蓝球的个数为1；‎ ‎（2）画树状图得：‎ ‎∵共有12种等可能的结果，两次都是摸到白球的有2种情况，‎ ‎∴两次都是摸到白球的概率为： =．‎ ‎　‎ ‎22．（7分）如图，将△ABC绕点C按顺时针方向旋转至△A′B′C，使点A′落在BC的延长线上．已知∠A=27°，∠B=40°，求则∠ACB′的度数．‎ ‎【解答】解：∵∠A=27°，∠B=40°，‎ ‎∴∠ACA′=∠A+∠B=27°+40°=67°，‎ ‎∵△ABC绕点C按顺时针方向旋转至△A′B′C，‎ ‎∴△ABC≌△A′B′C，‎ ‎∴∠ACB=∠A′CB′，‎ ‎∴∠ACB﹣∠B′CA=∠A′CB﹣∠B′CA，‎ 即∠BCB′=∠ACA′，‎ ‎∴∠BCB′=67°，‎ ‎∴∠ACB′=180°﹣∠ACA′﹣∠BCB′=180°﹣67°﹣67°=46°．‎ ‎　‎ ‎23．（8分）如图，点A是直线AM与⊙O的交点，点B在⊙O上，BD⊥AM垂足为D，BD与⊙O交于点C，OC平分∠AOB，∠B=60°．‎ ‎（1）求证：AM是⊙O的切线；‎ ‎（2）若DC=2，求图中阴影部分的面积（结果保留π和根号）．‎ ‎【解答】解：（1）∵∠B=60°，‎ ‎∴△BOC是等边三角形，‎ ‎∴∠1=∠2=60°，‎ ‎∵OC平分∠AOB，‎ ‎∴∠1=∠3，‎ ‎∴∠2=∠3，‎ ‎∴OA∥BD，‎ ‎∴∠BDM=90°，∴∠OAM=90°，‎ ‎∴AM是⊙O的切线；‎ ‎（2）∵∠3=60°，OA=OC，‎ ‎∴△AOC是等边三角形，‎ ‎∴∠OAC=60°，‎ ‎∵∠OAM=90°，‎ ‎∴∠CAD=30°，‎ ‎∵CD=2，‎ ‎∴AC=2CD=4，‎ ‎∴AD=2，‎ ‎∴S阴影=S梯形OADC﹣S扇形OAC=（4+2）×2﹣=6﹣．‎ ‎　‎ ‎24．（10分）某商场试销一种成本为每件50元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于40%，经试销发现，销售量y（件）与销售单价x（元）符合一次函数y=kx+b，且x=60时，y=50；x=70时，y=40．‎ ‎（1）求一次函数y=kx+b的表达式；‎ ‎（2）若该商场获得利润为W元，试写出利润W与销售单价x之间的关系式；销售单价定为多少元时，商场可获得最大利润，最大利润是多少元？‎ ‎【解答】解：（1）根据题意得，‎ 解得：，‎ ‎∴一次函数的表达式为y=﹣x+110；‎ ‎（2）W=（x﹣50）（﹣x+100）=﹣x2+160x﹣5500，‎ ‎∵销售单价不低于成本单价，且获利不得高于40%，即50≤x≤50×（1+40%），‎ ‎∴50≤x≤70，‎ ‎∵当x=﹣=80时不在范围内，‎ ‎∴当x=70时，W最大=800元，‎ 答：销售单价定为70元时，商场可获得最大利润，最大利润是800元．‎ ‎　‎ ‎25．（10分）阅读资料：我们把顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角，如图1中∠ABC所示．同学们研究发现：P为圆上任意一点，当弦AC经过圆心O时，且AB切⊙O于点A，此时弦切角∠CAB=∠P（图2）．‎ 证明：∵AB切⊙O于点A，∴∠CAB=90°，又∵AC是直径，∴∠P=90°，∴∠CAB=∠P 问题拓展：若AC不经过圆心O（如图3），该结论：弦切角∠CAB=∠P还成立吗？请说明理由．‎ 知识运用：如图4，AD是△ABC中∠BAC的平分线，经过点A的⊙O与BC切于点D，与AB、AC分别相交于E、F．求证：EF∥BC．‎ ‎【解答】解：问题拓展：∠CAB=∠P成立．理由如下：‎ 作直径AD，连接CD，如图3，则∠D=∠P，‎ ‎∵AD为直径，‎ ‎∴∠ACD=90°，‎ ‎∴∠D+∠CAD=90°，‎ ‎∵AB切⊙O于点A，‎ ‎∴AD⊥AB，‎ ‎∴∠CAB+∠CAD=90°，‎ ‎∴∠CAB=∠P；‎ 知识运用：如图4，连接DF，‎ ‎∵AD是△ABC中∠BAC的平分线，‎ ‎∴∠BAD=∠CAD，‎ ‎∵经过点A的⊙O与BC切于点D，‎ ‎∴∠CDF=∠CAD，‎ ‎∴∠BAD=∠CDF，[来源:Zxxk.Com]‎ ‎∵∠BAD=∠DFE，‎ ‎∴∠CDF=∠DFE，‎ ‎∴EF∥BC．‎ ‎　‎ ‎26．（14分）如图，二次函数y=ax2+bx+c（a≠0）的图象交x轴于A、B两点，交y轴于点D，点B的坐标为（3，0），顶点C的坐标为（1，4）．‎ ‎（1）求二次函数的解析式和直线BD的解析式；‎ ‎（2）点P是直线BD上的一个动点，过点P作x轴的垂线，交抛物线于点M，当点P在第一象限时，求线段PM长度的最大值；‎ ‎（3）在抛物线上是否存在异于B、D的点Q，使△BDQ中BD边上的高为2？若存在求出点Q的坐标；若不存在请说明理由．‎ ‎【解答】解：‎ ‎（1）∵抛物线的顶点C的坐标为（1，4），‎ ‎∴可设抛物线解析式为y=a（x﹣1）2+4，‎ ‎∵点B（3，0）在该抛物线的图象上，‎ ‎∴0=a（3﹣1）2+4，解得a=﹣1，‎ ‎∴抛物线解析式为y=﹣（x﹣1）2+4，即y=﹣x2+2x+3，‎ ‎∵点D在y轴上，令x=0可得y=3，‎ ‎∴D点坐标为（0，3），‎ ‎∴可设直线BD解析式为y=kx+3，‎ 把B点坐标代入可得3k+3=0，解得k=﹣1，‎ ‎∴直线BD解析式为y=﹣x+3；‎ ‎（2）设P点横坐标为m（m＞0），则P（m，﹣m+3），M（m，﹣m2+2m+3），‎ ‎∴PM=﹣m2+2m+3﹣（﹣m+3）=﹣m2+3m=﹣（m﹣）2+，‎ ‎∴当m=时，PM有最大值；‎ ‎（3）如图，过Q作QG∥y轴交BD于点G，交x轴于点E，作QH⊥BD于H，‎ 设Q（x，﹣x2+2x+3），则G（x，﹣x+3），‎ ‎∴QG=|﹣x2+2x+3﹣（﹣x+3）|=|﹣x2+3x|，‎ ‎∵△BOD是等腰直角三角形，‎ ‎∴∠DBO=45°，‎ ‎∴∠HGQ=∠BGE=45°，‎ 当△BDQ中BD边上的高为2时，即QH=HG=2，‎ ‎∴QG=×2=4，‎ ‎∴|﹣x2+3x|=4，‎ 当﹣x2+3x=4时，△=9﹣16＜0，方程无实数根，‎ 当﹣x2+3x=﹣4时，解得x=﹣1或x=4，‎ ‎∴Q（﹣1，0）或（4，﹣5），‎ 综上可知存在满足条件的点Q，其坐标为（﹣1，0）或（4，﹣5）．‎ ‎　‎